
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи движения точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поступательное движение твёрдого тела. Поступательное движение тела – такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельное самой себе. Основная теорема: При поступат. движ. все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Вращательное движение твёрдого тела. Угловая скорость и угловое ускорение.
Определение скоростей и ускорений точек твёрдого тела вращающегося вокруг неподвижной оси.
Вращ движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными.
Формулы Эйлера: wx,wy,wz – проекции вектора угловой скорости. Проекция вращательной (окружной) скорости: vx=wyz – wzy; vy=wzx – wxz; vz=wxy – wyx. Если ось вращения совпадает с осью z, то vx= – wy; vy=wx.
Ускорение:
26 Сложное движение точки. Основные определения. Примеры.
Сложение скоростей при сложном движении точки.
Сложение ускорений при сложном движении точки.
Ускорение Кориолиса. Численная величина и направление.
Плоскопараллельное движение твёрдого тела.
31. Способы определения скорости точки тела при плоском движении.
Мгновенный центр скоростей. Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. w¹0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в ¥. 33. Способы определения положения мгновенного центра скоростей
Ускорение точек при плоскопараллельном движении твёрдого тела.
Аксиомы динамики.
Дифференциальные уравнения движения точки. Две задачи динамики.
Первая (прямая) задача динамики. Пример.
Вторая (обратная) задача динамики. Пример.
Моменты инерции твердого тела. Радиус инерции
40. Теорема о моментах инерции твердого тела относительно параллельных осей (теорема Штейнера-Гюйгенса).
41. Дифференциальные уравнения движения механической системы и общие теоремы динамики Количество движения точки и системы. Импульс силы. Теорема об изменении количества движения. Следствия
Теорема о движении центра масс. Следствия.
Кинетический момент (момент количества движения) точки и системы. Кинетический момент относительно оси вращения при вращательном движении твердого тела.
Теорема об изменении кинетического момента точки и системы. Следствия.
Элементарная работа силы, работа силы на конечном пути. Работа силы тяжести.
Работа силы, приложенной к твердому телу.
Кинетическая энергия точки. Теорема об изменении кинетической энергии точки.
Кинетическая энергия точки, системы, твердого тела.
Теорема об изменении кинетической энергии точки и системы.
Принцип Даламбера для материальной точки и системы материальных точек.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.006 с.) |




 Скорости и ускорения точек вращающегося тела.
Скорости и ускорения точек вращающегося тела.  – скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.
– скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения. ,
, . Вращательное ускорение
. Вращательное ускорение 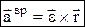 , модуль вращат. уск. авр=e×r×sina, направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение
, модуль вращат. уск. авр=e×r×sina, направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение  , ац=w2×R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.:
, ац=w2×R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.:  . Угол, между векторами полного и центростремит-ного ускорений:
. Угол, между векторами полного и центростремит-ного ускорений:  .
.





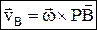 – скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры.
– скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры.  , скорости точек тела пропорциональны их расстояниям до м.ц.с.
, скорости точек тела пропорциональны их расстояниям до м.ц.с.  , угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с.
, угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с.





















