
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи движения точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1 Равномерное прямолинейное движение. При этом а = 0 (а t = 0, а n = 0, r = ¥), S = So + v×t (3.16) где So = S(0). 2 Равномерное криволинейное движение. При этом а = а n, a t = 0, v = const, уравнение движения описывается выражением (3.16). 3 Равномерное движение по окружности. При этом а = а n = const, a t = 0, 4 Переменное прямолинейное движение. При этом а = а t, а n= 0, так как r = ¥. Тогда
5 Переменное криволинейное движение.
В выражениях (3.17) и (3.18) знак (+) принимается в случае равноускоренного движения, знак (–) – равнозамедленного движения точки.
Последовательность решения задач по кинематике точки При решении задач по кинематике точки рекомендуется придерживаться следующей последовательности: 1 По заданным уравнениям движения точки определяем уравнение её траектории и указываем на этой кривой действительную траекторию точки. Для заданного момента времени находим положение точки на траектории. 2 Определяем скорость точки. 3 Определяем полное ускорение точки. 4 Определяем касательное и нормальное ускорения. 5 Определяем радиус кривизны траектории точки. 6 Вычислим указанные выше кинематические характеристики в заданный момент времени. Изображаем схематично векторы скорости, касательного, нормального, полного ускорений и радиус кривизны траектории, соответствующий для положения точки в данный момент времени.
Задача К1 Под номером К1 помещены две задачи К1а и К1б, которые надо решить. Задача К1а. Точка В движется в плоскости xy (рис. К1.0 – К1.9, таблица К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: x = f1(t), y = f2(t), где x, y выражены в сантиметрах, t – в секундах. Определить уравнение траектории точки для момента времени t1 = 1 с. Найти скорость и ускорение точки, касательное и нормальное её ускорения, а также радиус кривизны в соответствующей точке траектории. Зависимость x = f1(t) указана непосредственно на рисунках, а зависимость

Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону
 Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания её движения. Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания её движения.
В задаче все искомые величины нужно определить только для момента времени t1 = 1 с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные тригонометрические формулы: cos2a + sin2a = 1; cos 2a= cos2a – sin2a = 1 – 2sin2a = 2 cos2a –1; Пример К1а. Даны уравнения движения точки в плоскости xy:
(x, y – в сантиметрах, t – в секундах). Определить уравнение траектории точки для момента времени t = 1с. Найти скорость и ускорение точки, а также её нормальное и касательное ускорения и радиус кривизны в соответствующей точке траектории. Решение 1 Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Учитывая конкретный вид функции x = f1(t), y = f2(t), используем формулу: cos 2a= 1– 2 sin2a или Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (а). Получим
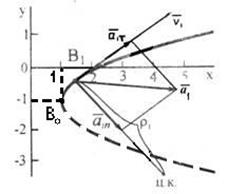
Следовательно, Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1а). x = (y+1)2 + 1 (б) Найдем начало отсчета движения, т.е. точку В0 (хо; уо) при to=0; хо=1, уо= -1, следовательно В0 (1;-1). Определим также координаты точки при t = 1с. x1 = –2cos(p/4) + 3 @ 1,5 (см), y1 = 2sin(p/8) – 1= – 0,23 см. Таким образом, точка движется от точки В0 к точке В1 и далее. Реализуется верхняя от точки В0 ветвь параболы. 2 Скорость точки найдем по её проекциям на координатные оси
где v1x, v1y, v1 – значения vx, vy, v при t = 1 с. 3 Аналогично находим ускорение:

где а 1х, а 1y, а 1 – значения а х, а у, а при t = 1 с. 4 Касательное ускорение при t = 1 с находим по формуле:
5 Нормальное ускорение при t = 1 с определяем из выражения:
6 При t = 1 с радиус кривизны траектории для точки В1 (1,5; –0,23) равен:
Ответ: v1 = 1,33 см/c, a 1 = 0,88 см/c2, a 1t = 0,66 см/c2, a 1n = 0,58 см/c2,
Пример К1б. Точка движется по дуге окружности радиуса R = 2 м по закону Решение Определяем скорость точки:
Полное ускорение находим по касательной и нормальной составляющим:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.007 с.) |

 (3.17)
(3.17) В этом случае
В этом случае (3.18)
(3.18)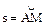 – расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы
– расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы  , считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М.
, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М.


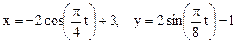
 (а)
(а)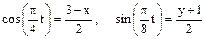
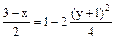 .
.

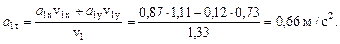
 .
.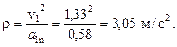
 и схематично r1 изображаем на рисунке К1а.
и схематично r1 изображаем на рисунке К1а. (S – в метрах, t – в секундах), где
(S – в метрах, t – в секундах), где  (рис. К1б). Определить скорость и ускорение в момент времени t1 = 1 с.
(рис. К1б). Определить скорость и ускорение в момент времени t1 = 1 с.
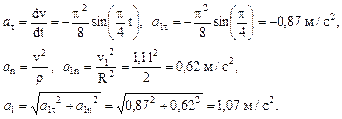
 Изобразим на рисунке К1б векторы
Изобразим на рисунке К1б векторы  , определив предварительно положение точки М на траектории при t1 = 1 с, которое характеризует дуговая координата
, определив предварительно положение точки М на траектории при t1 = 1 с, которое характеризует дуговая координата 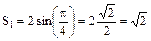 или центральный угол
или центральный угол  , иначе j = 40°30¢.
, иначе j = 40°30¢.


