
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные формулы для скоростей и ускорений точек телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скорость точки по модулю и направлению можно определить по формуле Эйлера векторным произведением:
где
Из определения ускорения и векторной формулы Эйлера имеем:
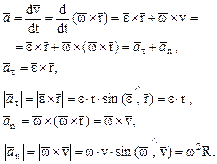 (3.29) (3.29)
Касательное и нормальное ускорения также можно записать в виде:
где Рассмотрим конкретные задачи.
Задача 3.1 Ротор мотора в период пуска имеет угловое ускорение e = 2p с–2. Определить скорость, касательное, нормальное и полное ускорения точки М Решение Угловую скорость ротора в момент времени t = 3 c находим, пользуясь формулой (3.25): w = wо + e×t
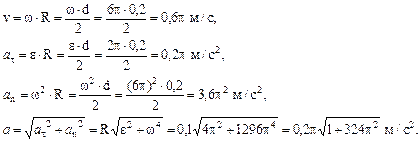
Векторы Задача 3.2 В период разгона маховика закон его вращения характеризуется Решение По формулам (3.21) и (3.22) определяем угловую скорость и угловое ускорение маховика.
Касательное и нормальное ускорения соответственно равны a t = e×R, a n = w2R. По условию задачи в момент времени t = t1 a t = a n. Поэтому в этот момент e = w2 или
Определим скорость и полное ускорение при t = t1
Задача 3.3 Шестерня 1 радиуса r1 приводится во вращение рукояткой АО1 = l. Эта шестерня сцеплена зубчатым колесом 2 радиуса r2, которое наглухо насажено на вал диаметра d. На вал намотан нерастяжимый канат, к которому прикреплен груз В. Определить скорость и ускорение груза В, если рукоятка АО1, вращаясь равноускоренно из состояния покоя совершает 16 оборотов за 2 с после начала движения (рис. 3.12).
Определяем угловое ускорение из формулы (3.25). По условию задачи jо = 0, Угловую скорость рукоятки для t = 2 с определяем по формуле (3.25) при Угловая скорость шестерни 1 равна угловой скорости рукоятки, так как они неизменно связаны между собой: w1 = w = 32p с–1 Скорость точки С, которая принадлежит к шестерне 1 и колесу 2, равна vC = w1r1 = w2r2, откуда Касательное ускорение а t(С) точки С находится по формуле (3.27)
Поскольку канат нерастяжим и вместе с грузом совершает поступательное движение, можно определить
Сложное движение точки В ряде случаев приходится рассматривать движение точки по отношению к системе координат O1x1y1z1, которая в свою очередь движется по отношению системы координат Oxyz, условно принятой в качестве неподвижной. При этом: 1) движение точки относительно системы координат Oxyz называется абсолютным; 2) движение точки относительно подвижной системы осей O1x1y1z1 называется относительным;
3) движение той точки подвижного пространства, с которой неизменно связана подвижная система отсчета O1x1y1z1 и с которой в данный момент времени совпадает рассматриваемая точка по отношению к неподвижной системе отсчета Oxyz называется переносным.
Разложение сложного (абсолютного) движения точки на относительные, переносные часто дает возможность привести сложное движение к простейшим движениям и этим самым облегчить решение конкретной задачи. Из определения абсолютного движения очевидно (рис. 3.13), что
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |


 (3.28)
(3.28) – радиус-вектор точки М, проведенной из произвольной точки оси вращения Oz, например точки О (рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.
– радиус-вектор точки М, проведенной из произвольной точки оси вращения Oz, например точки О (рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.
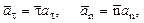
 – соответственно ортогональные единичные векторы (см. выше 3.1.2).
– соответственно ортогональные единичные векторы (см. выше 3.1.2). Здесь и далее учитываем, что вращение ротора равноускоренное, начальный угол поворота jо= 0 и начальная угловая скорость wо = 0, так как ротор начинает вращаться из состояния покоя. Тогда w = e×t = 2p×3 = 6p с–2. Для определения положения точки на ободе ротора вычислим также по формуле (3.24) угол поворота
Здесь и далее учитываем, что вращение ротора равноускоренное, начальный угол поворота jо= 0 и начальная угловая скорость wо = 0, так как ротор начинает вращаться из состояния покоя. Тогда w = e×t = 2p×3 = 6p с–2. Для определения положения точки на ободе ротора вычислим также по формуле (3.24) угол поворота 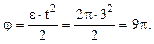 По формулам (3.27) определим соответственно скорость, касательное, нормальное и полное ускорение точки М.
По формулам (3.27) определим соответственно скорость, касательное, нормальное и полное ускорение точки М. в момент времени t = 3 c изображены на рисунке 3.11.
в момент времени t = 3 c изображены на рисунке 3.11. . Определить скорость и ускорение точки, находящейся на расстоянии
. Определить скорость и ускорение точки, находящейся на расстоянии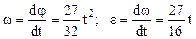
 откуда
откуда 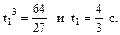 Подставляя t1 в выражения для e и w, находим, что в момент времени t1
Подставляя t1 в выражения для e и w, находим, что в момент времени t1


 . Отсюда
. Отсюда 

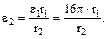 Так как колесо 2 и вал жестко скреплены, имеем:
Так как колесо 2 и вал жестко скреплены, имеем:


 (3.30)
(3.30)


