
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение, эффективность, загрузка и качествоСодержание книги
Поиск на нашем сайте
Рассмотрим параллельное выполнение программы со следующими характеристиками: · О(п) — общее число операций (команд), выполненных на п-процессорной системе; · Т(п) — время выполнения O(п) операций на «-процессорной системе в виде числа квантов времени. В общем случае Т(п) < O(п), если в единицу времени п процессорами выполняется более чем одна команда, где п > 2. Примем, что в однопроцессорной системе T(1) = O(1). Ускорение (speedup), или точнее, среднее ускорение за счет параллельного выполнения программы — это отношение времени, требуемого для выполнения наилучшего из последовательных алгоритмов на одном процессоре, и времени параллельного вычисления на п процессорах. Без учета коммуникационных издержек ускорение S(n) определяется как
Как правило, ускорение удовлетворяет условию S(n) < п. Эффективность (efficiency) n -процессорной системы — это ускорение на один процессор, определяемое выражением
Эффективность обычно отвечает условию 1/п ≤ Е(п) ≤ п. Для более реалистичного описания производительности параллельных вычислений необходимо промоделировать ситуацию, когда параллельный алгоритм может потребовать больше операций, чем его последовательный аналог. Довольно часто организация вычислений на п процессорах связана с существенными издержками. Поэтому имеет смысл ввести понятие избыточности (redundancy) в виде
Это отношение отражает степень соответствия между программным и аппаратным параллелизмом. Очевидно, что 1 < R(n) < п. Определим еще одно понятие, коэффициент полезного использования или утилизации (utilization), как
Тогда можно утверждать, что
Рассмотрим пример. Пусть наилучший из известных последовательных алгоритмов занимает 8с, а параллельный алгоритм занимает на пяти процессорах 2с. Тогда: · S(n) = 8/2 = 4; · E(n) = 4/5 = 0,8; · R(n) = 1/0,8 – 1 = 0,25. Собственное ускорение определяется путем реализации параллельного алгоритма на одном процессоре. Если ускорение, достигнутое на п процессорах, равно п, то говорят, что алгоритм показывает линейное ускорение. В исключительных ситуациях ускорение S(n) может быть больше, чем п. В этих случаях иногда применяют термин суперлинейное ускорение. Данное явление имеет шансы на возникновение в двух следующих случаях: Последовательная программа может выполняться в очень маленькой памяти, вызывая свопинги (подкачки), или, что менее очевидно, может приводить к большему числу кэш-промахов, чем параллельная версия, где обычно каждая параллельная часть кода выполняется с использованием много меньшего набора данных. Другая причина повышенного ускорения иллюстрируется примером. Пусть нам нужно выполнить логическую операцию А1 v А2, где как А1, так и А2 имеют значение «Истина» с вероятностью 50%, причем среднее время вычисления Аi, обозначенное как T(Аi), существенно различается в зависимости от того, является ли результат истинным или ложным. Пусть T(Аi)= 1c для Аi = 1; T(Аi)= 100c для Аi = 0. Теперь получаем четыре равновероятных случая (Т — «истина», F — «ложь», таблица 9).
Таким образом, параллельные вычисления на двух процессорах ведут к среднему ускорению:
Отметим, что суперлинейное ускорение вызвано жесткостью последовательной обработки, так как после вычисления еще нужно проверить A2. К факторам, ограничивающим ускорение, следует отнести: · Программные издержки. Даже если последовательные и параллельные алгоритмы выполняют одни и те же вычисления, параллельным алгоритмам присущи добавочные программные издержки — дополнительные индексные вычисления, неизбежно возникающие из-за декомпозиции данных и распределения их по процессорам; различные виды учетных операций, требуемые в параллельных алгоритмах, но отсутствующие в алгоритмах последовательных. · Издержки из-за дисбаланса загрузки процессоров. Между точками синхронизации каждый из процессоров должен быть загружен одинаковым объемом работы, иначе часть процессоров будет ожидать, пока остальные завершат свои операции. Эта ситуация известна как дисбаланс загрузки. Таким образом, ускорение ограничивается наиболее медленным из процессоров. · Коммуникационные издержки. Если принять, что обмен информацией и вычисления могут перекрываться, то любые коммуникации между процессорами снижают ускорение. В плане коммуникационных затрат важен уровень гранулярности, определяющий объем вычислительной работы, выполняемой между коммуникационными фазами алгоритма. Для уменьшения коммуникационных издержек выгоднее, чтобы вычислительные гранулы были достаточно крупными и доля коммуникаций была меньше. Еще одним показателем параллельных вычислений служит качество параллельного выполнения программ — характеристика, объединяющая ускорение, эффективность и избыточность. Качество определяется следующим образом:
Поскольку как эффективность, так и величина, обратная избыточности, представляют собой дроби, то Q(n) < S(n). Поскольку Е(п) — это всегда дробь, a R(n) — число между 1 и п, качество Q(n) при любых условиях ограничено сверху величиной ускорения S(n).
Закон Амдала
Приобретая для решения своей задачи параллельную вычислительную систему, пользователь рассчитывает на значительное повышение скорости вычислений за счет распределения вычислительной нагрузки по множеству параллельно работающих процессоров. В идеальном случае система из п процессоров могла бы ускорить вычисления в п раз. В реальности достичь такого показателя по ряду причин не удается. Главная из этих причин заключается в невозможности полного распараллеливания ни одной из задач. Как правило, в каждой программе имеется фрагмент кода, который принципиально должен выполняться последовательно и только одним из процессоров. Это может быть часть программы, отвечающая за запуск задачи и распределение распараллеленного кода по процессорам, либо фрагмент программы, обеспечивающий операции ввода/вывода. Можно привести и другие примеры, но главное состоит в том, что о полном распараллеливании задачи говорить не приходится. Известные проблемы возникают и с той частью задачи, которая поддается распараллеливанию. Здесь идеальным был бы вариант, когда параллельные ветви программы постоянно загружали бы все процессоры системы, причем так, чтобы нагрузка на каждый процессор была одинакова. К сожалению, оба этих условия на практике трудно реализуемы. Таким образом, ориентируясь на параллельную ВС, необходимо четко сознавать, что добиться прямо пропорционального числу процессоров увеличения производительности не удастся, и, естественно, встает вопрос о том, на какое реальное ускорение можно рассчитывать. Ответ на этот вопрос в какой-то мере дает закон Амдала. Джин Амдал (Gene Amdahl) — один из разработчиков всемирно известной системы IBM 360, в своей работе, опубликованной в 1967 году, предложил формулу, отражающую зависимость ускорения вычислений, достигаемого на многопроцессорной ВС, от числа процессоров и соотношения между последовательной и параллельной частями программы. Показателем сокращения времени вычислений служит такая метрика, как «ускорение». Напомним, что ускорение S — это отношение времени Ts, затрачиваемого на проведение вычислений на однопроцессорной ВС (в варианте наилучшего последовательного алгоритма), ко времени Тр решения той же задачи на параллельной системе (при использовании наилучшего параллельного алгоритма):
Оговорки относительно алгоритмов решения задачи сделаны, чтобы подчеркнуть тот факт, что для последовательного и параллельного решения лучшими могут оказаться разные реализации, а при оценке ускорения необходимо исходить именно из наилучших алгоритмов. Проблема рассматривалась Амдалом в следующей постановке (рис. 87). Прежде всего, объем решаемой задачи с изменением числа процессоров, участвующих в ее решении, остается неизменным. Программный код решаемой задачи состоит из двух частей: последовательной и распараллеливаемой. Обозначим долю операций, которые должны выполняться последовательно одним из процессоров, через f, где 0 ≤ f ≤ 1 (здесь доля понимается не по числу строк кода, а по числу реально выполняемых операций). Отсюда доля, приходящаяся на распараллеливаемую часть программы, составит 1 – f. Крайние случаи в значениях/соответствуют полностью параллельным (f = 0) и полностью последовательным (f = 1) программам. Распараллеливаемая часть программы равномерно распределяется по всем процессорам.
Рис. 87. К постановке задачи в законе Амдала.
С учетом приведенной формулировки имеем:
В результате получаем формулу Амдала, выражающую ускорение, которое может быть достигнуто на системе из n процессоров:
Формула выражает простую и обладающую большой общностью зависимость. Если устремить число процессоров к бесконечности, то в пределе получаем:
Это означает, что если в программе 10% последовательных операций (то есть f =0,1), то, сколько бы процессоров ни использовалось, убыстрения работы программы более чем в десять раз никак ни получить, да и то, 10 — это теоретическая верхняя оценка самого лучшего случая, когда никаких других отрицательных факторов нет. Следует отметить, что распараллеливание ведет к определенным издержкам, которых нет при последовательном выполнении программы. В качестве примера таких издержек можно упомянуть дополнительные операции, связанные с распределением программ по процессорам, обмен информацией между процессорами и т. д.
Закон Густафсона
Известную долю оптимизма в оценку, даваемую законом Амдала, вносят исследования, проведенные уже упоминавшимся Джоном Густафсоном из NASA Ames Research. Решая на вычислительной системе из 1024 процессоров три больших задачи, для которых доля последовательного кода лежала в пределах от 0,4 до 0,8%, он получил значения ускорения по сравнению с однопроцессорным вариантом, равные соответственно 1021,1020 и 1016. Согласно закону Амдала для данного числа процессоров и диапазона f, ускорение не должно было превысить вели чины порядка 201. Пытаясь объяснить это явление, Густафсон пришел к выводу, что причина кроется в исходной предпосылке, лежащей в основе закона Амдала: увеличение числа процессоров не сопровождается увеличением объема решаемой задачи. Реальное же поведение пользователей существенно отличается от такого представления. Обычно, получая в свое распоряжение более мощную систему, пользователь не стремится сократить время вычислений, а, сохраняя его практически неизменным, старается пропорционально мощности ВС увеличить объем решаемой задачи. И тут оказывается, что наращивание общего объема программы касается главным образом распараллеливаемой части программы. Это ведет к сокращению значения f. Примером может служить решение дифференциального уравнения в частных производных. Если доля последовательного кода составляет 10% для 1000 узловых точек, то для 100 000 точек доля последовательного кода снизится до 0,1%. Сказанное иллюстрирует рис. 88, который отражает тот факт, что, оставаясь практически неизменной, последовательная часть в общем объеме увеличенной программы имеет уже меньший удельный вес.
Рис. 88. К постановке задачи в законе Густафсона.
Было отмечено, что в первом приближении объем работы, которая может быть произведена параллельно, возрастает линейно с ростом числа процессоров в системе. Для того чтобы оценить возможность ускорения вычислений, когда объем последних увеличивается с ростом количества процессоров в системе (при постоянстве общего времени вычислений), Густафсон рекомендует использовать выражение, предложенное Е. Барсисом (Е. Barsis):
Данное выражение известно как закон масштабируемого ускорения или закон Густафсона (иногда его называют также законом Густафсона-Барсиса). В заключение отметим, что закон Густафсона не противоречит закону Амдала. Различие состоит лишь в форме утилизации дополнительной мощности ВС, возникающей при увеличении числа процессоров.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.008 с.) |

 .
.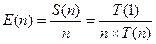 .
. .
. .
. и
и 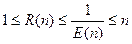 .
.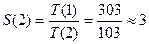 .
. .
. .
.
 .
.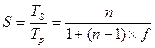 .
. .
.
 .
.


