
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении кинетической энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема об изменении кинетической энергии точки. В основе этой теоремы, как и рассмотренных выше теорем, лежит второй закон Ньютона. Проектируя равенство 4.1 на касательную ось получим:
Касательное ускорение запишем в формуле:
где ds – элементарное перемещение точки (рис. 4.2). В результате найдем, что
где Работа на конечном перемещении точки
 (4.39) (4.39)
или Единицей измерения работы в СИ является – 1 джоуль (1 дж.=1 кН). Величина
есть мощность силы (1 Вт= 1 дж/с). Равенство (4.37) есть выражения теоремы об изменении кинетической энергии в дифференциальной форме. Можно записать выражение теоремы в конечном виде.
Теорема. Изменения кинетической энергии точки на некотором перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении. Теорема об изменении кинетической энергии системы Для k -ой точки системы можно записать
Где
Равенство (4.43.) выражает теорему об изменении кинетической энергии в дифференциальной форме. Проинтегрировав это равенство в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна
Это уравнение выражает теорему об изменении кинетической энергии в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных в системе внешних и внутренних сил. Частные случаи. 1.Неизменяемая система. В случае неизменяемой системы сумма работ всех внутренних сил равно нулю
2. Система с идеальными связями. В этом случае
Здесь 1. Работа силы тяжести
где Р – вес системы, 2. Работа силы упругости пружины
где с – коэффициент жесткости пружины, λ– удлинение пружины. 3. Работа силы трения
где f – коэффициент трения, N – нормальная реакция поверхности. 4. Работа сил и пар сил, приложенных к вращающемуся телу. Элементарная работа момента силы или момента пары относительно оси вращения равна
где При повороте на конечный угол
и в случае постоянного момента
В этом случае мощность определяется по формуле
В задаче Д3 используется теорема об изменении кинетической энергии системы.
Задача Д3 Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д3.0 – Д3.9 табл. Д3); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с. Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках). Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: ν1, ν2, νС5 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости 3 и 4. Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис.2), катятся по плоскости без скольжения. На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.

Указания. Задача Д3 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек теля, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Система приходят в движение из состояния покоя под действием силы F = f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие не систему внешние силы: активные Для определения ω3 воспользуемся теоремой об изменении кинетической энергии:
2. Определяем Т0 и Т. Так как в начальный момент система находилась в покое, то Т0 = 0. Величина Т равна сумме энергий всех тел системы:
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
Все входящие сюда скорости надо выразить через искомую ω3. Для этого предварительно заметим, что νС1 = ν5 = νА, где А – любая точка обода радиуса r3 шкива 3 и что точка К1 – мгновенный центр скоростей катка 1, радиус которого обозначим r1. Тогда νС1 = ν5 = ω3r3; Кроме того, входящие в (3) моменты инерции имеют значения
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь s1. Введя обозначения: s5 – перемещение груза 5 (s1 = s5), φ3 – угол поворота шкива 3, λ0 и λ1 – начальное и конечное удлинения пружины, получим
Работы остальных сил равны нулю, так как точки К1 и К2, где приложены силы По условиям задачи, λ0 = 0. Тогда λ1 = sE, где sE – перемещение точки Е (конца пружины). Величина sE и φ3 надо выразить через заданное перемещение s1; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда так как ω3 = νА / r3 = νC1 / r3 (равенство νС1 = νА уже отмечалось), то и φ3 = s1 / r3. Далее, из рис. Д3,б видно, что νD = νB = ω3R3, а так как точка К2 является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку К2L), то νЕ = 0,5νD = 0,5ω3R3; следовательно, и λ1 = sE = 0,5φ3R3 = 0,5s1R3 / r3. При найденных значениях φ3 и λ1 для суммы вычисленных работ получим
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т0 = 0, придем к равенству
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость ω3. Ответ: ω3 = 8,1 с -1.
Принцип Даламбера Наряду с общими теоремами динамики позволяют найти эффективные методы решения задач принципы механики, которые также базируются на законах Ньютона-Галилея. Рассмотрим основное уравнение динамики (4.1.) для несвободной материальной точки в форме.
где
при этом введем в рассмотрение величину
В этом заключается принцип Даламбера: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.108 (0.009 с.) |


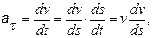
 , или
, или  , или
, или  (4.37)
(4.37) Здесь
Здесь  - кинетическая энергия,
- кинетическая энергия,  - элементарная работа силы Fкτ (рис. 4.2). Элементарная работа силы
- элементарная работа силы Fкτ (рис. 4.2). Элементарная работа силы  также может быть представлена в виде
также может быть представлена в виде (4.38),
(4.38),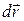 - дифференциал радиуса-вектора точки,
- дифференциал радиуса-вектора точки, 
 может быть вычислена как предел интегральной суммы.
может быть вычислена как предел интегральной суммы. (4.40)
(4.40) (4.41)
(4.41) . Единица измерения мощности в СИ – ватт
. Единица измерения мощности в СИ – ватт (4.42)
(4.42)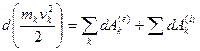 , (к = 1,2,…,4)
, (к = 1,2,…,4)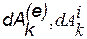 - элементарные работы приложенных к точке внешних и внутренних сил. Суммируя это выражение по k=1,2,3…, n, найдем, что
- элементарные работы приложенных к точке внешних и внутренних сил. Суммируя это выражение по k=1,2,3…, n, найдем, что или
или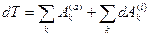 (4.43)
(4.43) в положение, где
в положение, где  , получим
, получим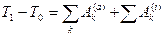 (4.44)
(4.44) или
или (4.45)
(4.45) и поскольку
и поскольку  ,
, (4.46)
(4.46) - суммы работ активных сил и реакций связей. Примеры вычисления работы.
- суммы работ активных сил и реакций связей. Примеры вычисления работы.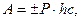
 - вертикальное перемещение центра масс системы.
- вертикальное перемещение центра масс системы.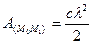

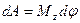
 - вращающий момент.
- вращающий момент.

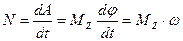
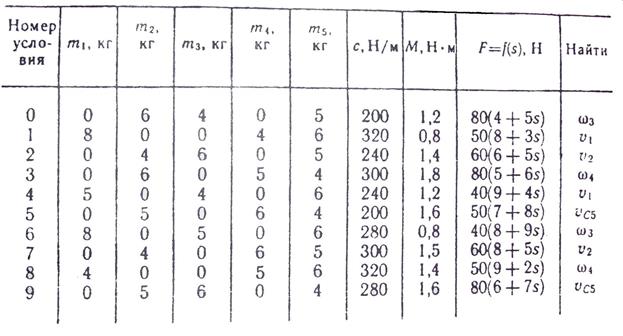





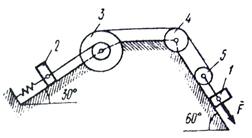
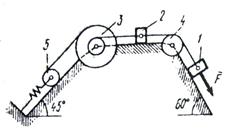

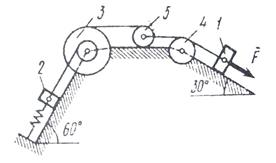

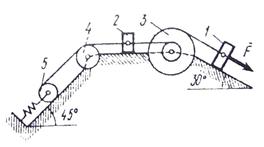
 Пример Д6. Механическая система (рис. Д3, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости С; ее начальная деформация равна нулю.
Пример Д6. Механическая система (рис. Д3, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости С; ее начальная деформация равна нулю. ,
,  ,
,  ,
,  ,
, 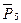 , реакции
, реакции  ,
,  ,
, 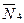 ,
,  , натяжение нити
, натяжение нити  , силы трения
, силы трения 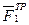 ,
,  и момент М.
и момент М. (1)
(1) (2)
(2)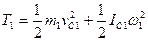 ;
; ;
; 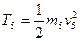 (3)
(3) (4)
(4) ;
;  (5)
(5) (6)
(6)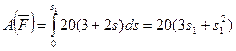 ;
; ;
; ;
; ;
;
 ,
,  - неподвижны; а реакция
- неподвижны; а реакция  (7)
(7)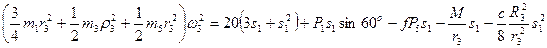 (8)
(8) , (4.47)
, (4.47)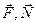 - активная сила и реакция связи соответственно. Запишем выражение (4.47.) в виде
- активная сила и реакция связи соответственно. Запишем выражение (4.47.) в виде
 , которую назовем силой инерции. Она направлена противоположно ускорению точки. На что указывает знак (-) Тогда
, которую назовем силой инерции. Она направлена противоположно ускорению точки. На что указывает знак (-) Тогда (4.48)
(4.48)


