Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия механической системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинетической энергий механической системы называется скалярная величина, равная арифметической сумме кинетических энергий точек данной системы, т.е.:
Следует отметить, что кинетическая энергия механической системы: - является величиной заведомо положительной; - характеризует и поступательную и вращательную составляющие движения системы; - внутренние силы влияют на значения кинетической энергии точек системы и, поэтому, изменяют кинетическую энергию всей системы. Если в механическую систему входят тела, то величина ее кинетической энергии может быть найдена как сумма кинетических энергий отдельных тел:
В выражение (14.75) входит знак суммы, что в общем случае подразумевает трудоемкий процесс суммирования большого числа слагаемых. Для некоторых типов движения механических систем (тел) можно предложить достаточно простые выражения. Найдем эти формулы.
Поступательное движение механической системы В этом случае все точки системы движутся с одинаковыми скоростями (свойства поступательного движения тела). Поэтому, выражение (14.75) можно преобразовать, вынеся за знак суммы постоянные величины:
или:
Таким образом, кинетическая энергия механической системы при ее поступательном Движении равна половине произведения массы системы на квадрат ее скорости.
Вращательное движение механической системы
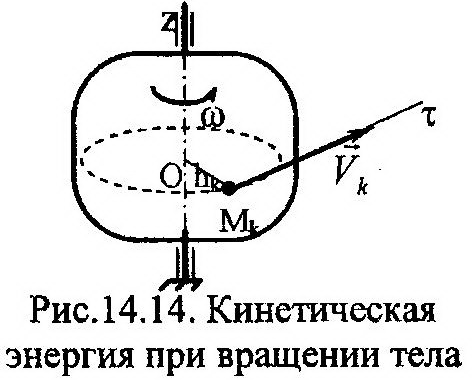
Рассмотрим тело (рис. 14.14), совершающее вращательное движение относительно вертикальной оси z. Представим это тело как механическую систему точек. Найдем для него формулу кинетической энергии, используя выражение (14.75), получим:
Кинетическая энергия механической системы при ее вращательном движении равна половине произведения ее момента инерции, взятого относительно оси вращения, на квадрат угловой скорости. Сравнивая формулы (14.78) и (14.80), нетрудно заметить, что между ними имеет место прямая аналогия. Действительно, в обоих случаях величина кинетической энергии определяется как половина произведения меры инертности тела (масса или момент инерции) на квадрат ее скорости.
Плоскопараллельное движение механической системы
Ранее было показано, что плоское движение тела можно представить как геометрическую сумму двух движений: поступательного и вращательного. Поэтому, кинетическая энергия системы при ее плоском движении может быть найдена по формуле:
где Vc – скорость центра масс механической системы; Icz – момент инерции механической системы относительно оси, проходящей через ее центр масс. Найдем выражение, определяющее изменение величины кинетической энергии механической системы. Для этого докажем теорему об изменении кинетической энергии механической системы. Рассмотрим механическую систему, состоящую из n материальных точек. Все силы, действующие на точки системы, разделим на внешние и внутренние. Таким образом, к каждой точке будут приложены по две сходящиеся системы сил: внешних и внутренних.
женных к произвольной k -й точке механической системы соответственно. Тогда выражение (14.72) теоремы об изменении кинетической энергии k-й точки запишется в следующем виде:
Очевидно, что такое же выражение можно записать для всех n точек системы. В результате получим систему n уравнений вида (14.82). Сложим почленно эти уравнения, получим:
или:
Выражение (14.84) отражает теорему об изменении кинетической энергии механической системы, записанную в дифференциальной форме. Взяв интегралы от обеих частей (14.84), можно получить выражение этой же теоремы, записанное в интегральном виде:
где Т0, Т1 – значения кинетической энергии системы в начальный и конечный моменты времени, т.е.: изменение кинетической энергии механической системы при некотором ее пере-
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 828; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.106.176 (0.006 с.) |





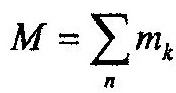
 или:
или: