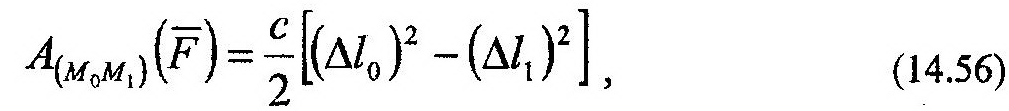Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении кинетического моментаСодержание книги
Поиск на нашем сайте
Для вывода теоремы об изменении кинетического момента механической системы воспользуемся выражением (14.33), отражающим изменение момента количества движения точки. Механическую систему представим как совокупность n материальных точек (рис. 14.2). При этом классифицируем все силы на внешние и внутренние. Для произвольной k -й точки правая часть выражения (14.33) примет следующий вид:
Для каждой точки механической системы можно составить выражение (14.44), где индекс k примет свое значение, соответствующее номеру точки (k=1…n). Таким образом получим систему, состоящую из n дифференциальных уравнений вида (14.44). Сложим почленно эти уравнения, получим:
Согласно второму свойству внутренних сил механической системы последнее слагаемое (14.45) равно нулю, а в левой части, под знаком дифференциала, имеем выражение кинетического момента (14.40). С учетом этого выражение (14.45) можно переписать в виде:
что и отражает теорему об изменении кинетического момента механической системы, а именно: производная по времени от кинетического момента механической системы, определенного относительно произвольного неподвижного центра, равна геометрической сумме моментов всех внешних сил относительно того же центра. Проектируя (14.46) на координатные оси, получим выражение теоремы в скалярной форме записи. Например, на ось х:
Практическая ценность этих выражений заключается в том, что при их использовании нет необходимости учитывать внутренние силы системы. Частным случаем доказанной теоремы является закон сохранения кинетического момента механической системы, который может иметь место, когда:
менем ни по величине, ни по направлению.
ет свое значение относительно данной оси.
ЛЕКЦИЯ 14. Кинетическая энергия. Работа Работа силы
Понятие работы силы связывает два фундаментальных понятия: сила и энергия. Введем сначала понятие элементарной работы силы:
ся положительный, если угол α между вектором силы, F, и скоростью, V, точки приложе-ния силы – острый. В противном случае, работа силы будет отрицательной. Другими словами, если сила увеличивает модуль скорости, то работа этой силы положитель-ная, и наоборот. Выражение (14.48) используют при естественном способе задания движения точки. При использовании векторного способа параметр, определяющий положение точки, является радиус-вектором, r. Нетрудно показать, что элементарное изменение дуговой координаты, dS, эквивалентно элементарному перемещению, dr. Тогда, используя (14.49), получим:
т.е. элементарная работа силы равна скалярному произведению вектора силы на век- Тор элементарного перемещения точки ее приложения. Решение задач в декартовой системе координат ведет к использованию проекций различных векторов на оси x, y, z. Выражение элементарной работы, в этом случае, можно
Работа силы на конечном перемещении точки равна интегралу от соответствующего выражения элементарной работы (14.49)-(14.51). В аналитической форме:
Мощностью называют величину, равную работе силы за единицу времени, т.е.:
V – скорость движения точки приложения силы. Единицами измерения работы является [Дж], а мощности - [Вт]. Найдем выражения работы для наиболее часто встречающихся сил.
Работа силы тяжести
Пусть точка М движется по некоторой траектории под действием силы тяжести Р (РИС. 14.9). Определим работу этой силы на перемещении М0М1. Воспользуемся выражением (14.52), получим:
(14.54) следует, что значение работы силы тяжести не зависит от вида самой траектории. Силы, обладающие таким свойством, называются потенциальными.
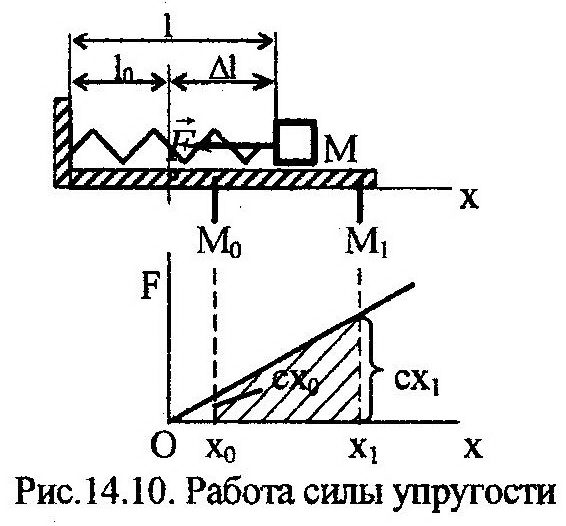
Работа силы упругости
Примером такой силы является реакция пружины на ее деформацию. На рис. 14.10 показано тело М, к которому крепится пружина длиною l0.
где Δl0, Δl1 – начальная и конечная деформация пружины. Сила упругости пружины, как видно из (14.56), также является потенциальной силой.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.124.123 (0.005 с.) |






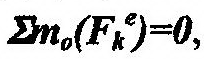


 или, учитывая, что Fτ=Fcosα, получим:
или, учитывая, что Fτ=Fcosα, получим:
 где dS – бесконечно малое перемещение точки М, показан-
ное на рис. 14.7.
Учитывая неоднозначность косинуса, знак работы получит-
где dS – бесконечно малое перемещение точки М, показан-
ное на рис. 14.7.
Учитывая неоднозначность косинуса, знак работы получит-



 Остальные шесть величин равны нулю, т.к. составляющие силы на нормально ориентированных перемещениях выполнить работу не могут, т.е.:
Остальные шесть величин равны нулю, т.к. составляющие силы на нормально ориентированных перемещениях выполнить работу не могут, т.е.: