
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа внутренних сил твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Представим твердое тело как совокупность материальных точек, определенным образом связанных друг с другом. Зададим телу элементарное перемещение в пространстве. При этом все его точки совершат собственные элементарные перемещения. Рассмотрим две произвольные точки: j и k (рис. 14.11), положение которых определяют радиусы-векторы rj и rk. Элементарные перемещения этих точек будут drj и drk. Силы взаимодействия меж-ду точками любой пары, согласно III закону динамики, равны по модулю и противопо-ложны по направлению, т.е.:
Произвольное элементарное перемещение всего тела можно представить как геометрическая сумма поступательного и сферического перемещений. Тогда элементарное перемещение точки k будет равно:
Определим величину суммы работ внутренних сил взаимодействия указанных на рисунке точек. Воспользуемся для этого выражением (14.50), получим:
Произведем небольшие преобразования последнего слагаемого (14.59), учитывая (14.57) и (14.58), получим:
ных работ, указанных на рис. 14.11, внутренних сил будет равна нулю:
Так как каждой внутренней силе найдется такая же по величине, но противоположная по направлению другая внутренняя сила, то сумма элементарных работ всех внутренних сил твердого тела будет равна нулю, т.е.:
Аналогичный результат можно получить при определении суммы работ внутренних сил твердого тела, совершаемых на конечном перемещении. Действительно, работа силы на конечном перемещении можно представить как предел суммы элементарных работ.
или: сумма работ внутренних сил твердого тела на любом его перемещении равна ну- Лю.
Работа вращающего момента
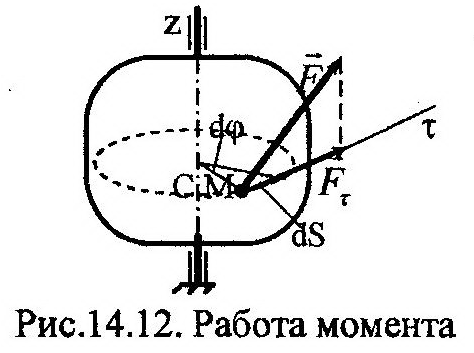
Определим работу вращающего момента MZ(F), создаваемого силой F, показанной на рис. 14.12. Элементарная работа этой силы будет равна:
В случае, если к телу приложена система сил, то выражение (14.65) можно записать в виде:
Работа вращающего момента на конечном угловом перемещении тела будет равен:
где φо, φ1 – начальная и конечная угловые координаты тела.
Кинетическая энергия точки
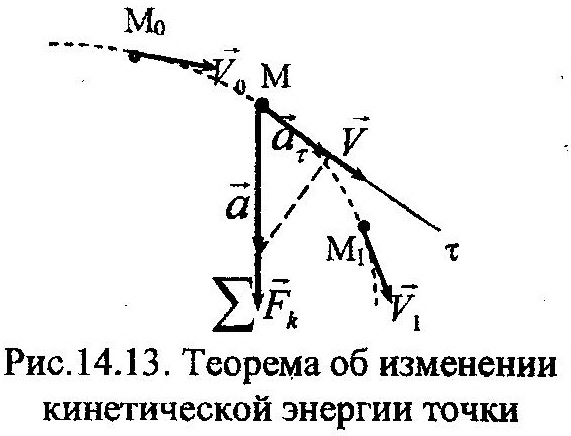
На, равная половине произведения ее массы на квадрат скорости точки. Пусть точка М перемещается под действием системы сил по некоторой траектории, как это показано на рис. 14.13. Найдем выражение, отражающее изменение кинетической энергии точки. Для этого воспользуемся основным законом динамики (11.1) и спроек-тируем обе части на касательную ось, получим:
Умножим обе части (14.70) на dS, получим:
Представим левую часть (14.71) в виде дифференциала кинетической энергии точки и учтем, что в правой части под знаком суммы стоит элементарная работа k -й силы. Учитывая все это, получим:
Выражение (14.72) отражает теорему об изменении кинетической энергии точки, пред-ставленную в дифференциальном виде. Оно показывает, что изменение кинетической энергии точки равно сумме элементар- Ных работ всех сил, приложенных к данной точке. Эта же теорема может быть записана в интегральном виде. Для этого необходимо взять интеграл от обеих частей (14.72). Учтем, что интеграл от суммы равен сумме интегралов, получим:
или:
Выражение (14.74) отражает теорему об изменении кинетической энергии точки, представленную в интегральном виде. Оно показывает, что изменение кинетической энергии точки на ее конечном перемеще- Нии равно сумме работ, выполняемых всеми приложенными к ней силами, на том же перемещении.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |



 где drj – элементарное перемещение точки k, соответ-ствующее поступательной составляющей перемещения всего тела;
dr – элементарное перемещение точки k, соответ-ствующее сферической составляющей перемещения всего тела.
где drj – элементарное перемещение точки k, соответ-ствующее поступательной составляющей перемещения всего тела;
dr – элементарное перемещение точки k, соответ-ствующее сферической составляющей перемещения всего тела.
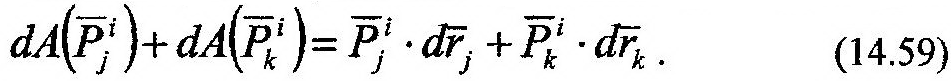
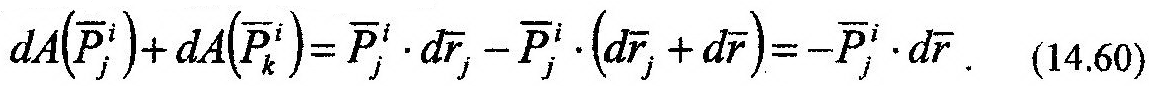






 где h=MC (см. рис. 14.12), а Fτh=Mz(F).
Тогда получим:
где h=MC (см. рис. 14.12), а Fτh=Mz(F).
Тогда получим:
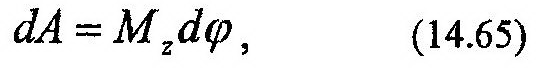 т.е.: элементарная работа вращающего момента силы
равна произведению его величины на элементарное приращение угловой координаты тела.
т.е.: элементарная работа вращающего момента силы
равна произведению его величины на элементарное приращение угловой координаты тела.


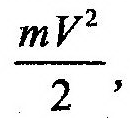
 Формула касательной составляющей ускорения может быть преобразована следующим образом:
Формула касательной составляющей ускорения может быть преобразована следующим образом:
 Подставим (14.69) в (14.68), получим:
Подставим (14.69) в (14.68), получим:








