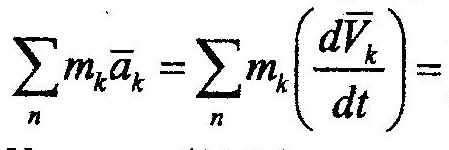Сумме сил, действующих на эту точку.

Выражение (14.9) представляет собой теорему об изменении количества движения точки,

записанную в векторной форме. При решении задач используют, как правило, скалярную форму записи данной теоремы в виде:

 

 

Выражение теоремы об изменении количества движения точки может быть представлено, также, в интегральном виде, если в (14.9) обе части умножить на dt и взять от полученного выражения интеграл (рис. 14.1), т.е.:

 

Под знаком суммы находится выражение импульса силы F_k за промежуток времени t_O … t_I.

Учитывая это, получим:

 

 

т.е., изменение количества движения точки за некоторый промежуток времени рав-

Но геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени.

В скалярной форме выражение данной теоремы можно получить если спроектировать обе части выражения (14.12) на координатные оси:

В случае движения точки по прямой для решения задачи достаточно воспользоваться одним из уравнений системы (14.13).

 

 

Количество движения механической системы

 

Количеством движения механической системы называют векторную величину, рав-

Ную геометрической сумме количеств движения всех точек данной системы,

т.е.:

 

На рис. 14.2 показана система n материальных точек, каждая из которых имеет свою величину количества движения, m_kV_k. Построив из этих векторов многоугольник, можно найти вектор суммы, Q, который и является вектором количества движения механической системы. Ясно, что вектор суммы может принимать любые значения и быть равным нулю. Выражение (14.14) отражает сущность данной характеристики движения механической системы, но не может быть рекомендовано для ее определения. Действительно, если механическая система представляет собой совокупность большого числа точек, то процесс определения Q окажется весьма трудоемким. Найдем другую формулу этой величины. Для этого воспользуемся векторным выражением (13.3), определяющим положение центра масс механической системы. Умножим обе части этой формулы на массу системы, М, получим:

 

Возьмем первую производную от обеих частей этого выражения. При этом учтем, что производная от суммы равна сумме производных, а масса точки и системы, как постоянные величины, могут быть вынесены за знак производной:

Производные от радиусов-векторов являются скоростями k -й точки и центра масс, поэтому выражение (14.16) перепишем в следующем виде:

 

 

Учитывая равенство правой части (14.14) и левой части (14.17), получим формулу для определения количества движения системы:

 

т.е.: количество движения механической системы равно произведению ее массы на

скорость центра масс.

Преимущество формулы (14.18) над выражением (14.14) очевидно, т.к. в (14.18) для определения Q требуется знать скорость только одной точки – центра масс. Интересно заметить, что в случае покоя этой точки, не зависимо от значений скоростей других точек системы, количество движения механической системы будет равно нулю. Таким образом,

Количество движения – это характеристика поступательной составляющей движе-

Ния механической системы.

 

Теорема об изменении количества движения

Механической системы

Рассмотрим механическую систему, состоящую из n материальных точек (рис. 13.2). Для вывода данной теоремы воспользуемся системой дифференциальных уравнений (13.6). Сложим почленно эти уравнения, получим:

Последняя сумма в (14.19) равна нулю по 1-му свойству внутренних сил. Левую же часть можно преобразовать следующим образом:

Учитывая (14.20), перепишем (14.19) в виде:

что и представляет собой векторную форму записи теоремы об изменении количества движения механической системы в дифференциальной форме, т.е.: производная по времени от количества движения механической системы равна геометрической сумме всех внешних сил, действующих на эту систему.

В скалярной форме эта теорема может быть записана в проекциях на координатные оси:

В конечном виде выражение теоремы можно получить как из выражения (14.21), так и из (14.22). Для этого необходимо разделить переменные и проинтегрировать эти выражения, получим:

или

 

где

–импульс внешней k -й силы.

 

Саму теорему на основе (14.24) можно формулировать следующим образом: