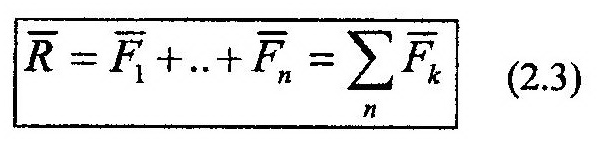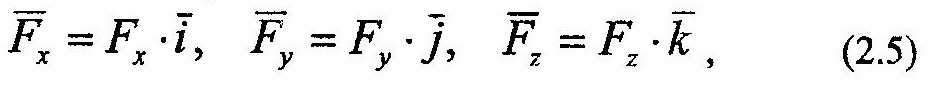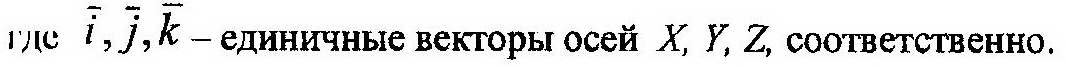Свободное атт может находиться в равновесии.

Эквивалентными системами сил являются такие системы, под действием которых

Тело может находиться в равновесии или совершать

Одинаковые движения.

Равнодействующей называется сила, эквивалентная по действию данной системе

Сил.

Аксиомы статики

Для вывода уравнений и теорем статики воспользуемся следующими исходными положениями, которые будут приняты без математических доказательств. Эти положения называют аксиомами статики.

Аксиома 1: если на свободное АТТ действуют две силы, то тело может находиться в

Равновесии только тогда, когда эти силы равны по модулю, и направлены по одной и той же прямой в противоположные стороны.

Аксиома 2: действие данной системы сил на АТТ не изменится, если к нему прило-

Жить или снять уравновешенную систему сил.

Следствие: действие силы на АТТ не изменится, если ее ее точку приложения перенести вдоль линии действия силы. Аксиома 3 (параллелограмм сил): две силы, приложенные к телу в одной точке, имеют равнодейству-ющую, приложенную в той же точке и изобра- жаемую диагональю параллелограмма, по- строенного на этих силах, как на сторонах(рис. 1.2)

 

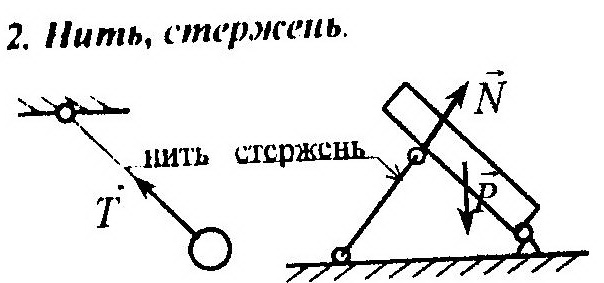
Аксиома 4: при всяком действии одного АТТ на другое имеет место такое же по вели-

Чине, но противоположное по направлению противодействие.

Связи и их реакции

Связями называется все то, что ограничивает перемещение данного тела в пространстве.

Силой реакции связи (реакцией связи) называется сила, с которой данная связь

Действует на тело, препятствуя тем или иным его перемещениям.

Активные силы – это силы, не являющиеся реакциями связей.

В основу методов решения задач на равновесие положена

аксиома связей: всякое несвободное тело можно рассматривать как свободное, если

Отбросить связи и заменить их действие соответствующими силами

Реакций.

Рассмотрим наиболее часто встречающиеся типы связей:

 

 

 

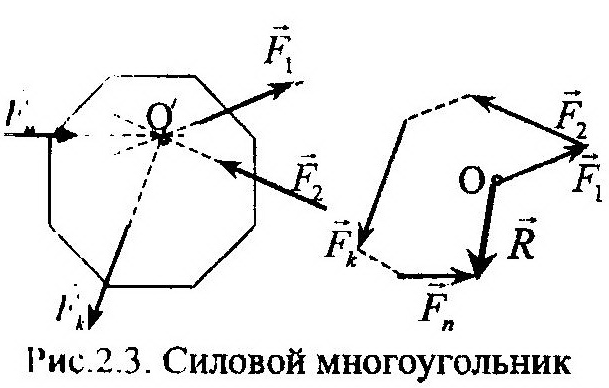
ЛЕКЦИЯ 2. СИСТЕМА СХОДЯЩИХСЯ СИЛ

Системой сходящихся сил (ССС) называют такую систему сил, линии действия которых пересекаются в одной той же точке.

Геометрический способ сложения сил

Главным вектором называется вектор, получаемый путем геометрического

Сложения ССС.

Сложение двух сил

Согласно аксиоме 3, геометрическое сложение осуществляется с помощью правила параллелограмма, что и показано на рисунке 2.1.

 

 

 

Сложение трех сил, не лежащих в одной плоскости, сводится к нахождению диагонали параллелепипеда (рис.2.2)

 

	Сложение произвольного числа сил осуществляется путем построения силового многоугольника (рис.2.3), построенного из приложенных к телу сил F1…Fn:

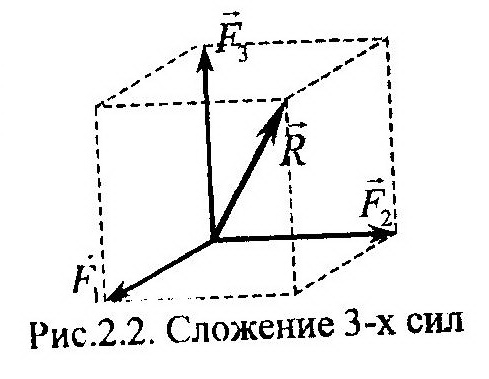
Разложение сил.

Разложить силу на составляющие – это означает найти такую ССС, главным

Вектором которой является исходная сила.

Очевидно, что этот процесс является обратным сложению сил. При решении задач наибольший практический интерес представляет разложение силы на две или три взаимно перпендикулярные составляющие (плоская или пространственная задача).

Проекцией силы на ось называется скалярная величина, равная длине отрезка,

С соответствующим знаком, заключенного между проекциями начала и конца силы на ту же ось.

Связь между составляющими и проекциями может быть определена следующими зависимостями:

 

Таким образом, вектор составляющей может быть получен путем умножения проекции на единичный вектор.

 

Аналитический способ сложения сил.

Аналитическое сложение ССС можно выполнить с помощью следующей теоремы:

 

Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Это означает, что если вектор суммы (например, равнодействующая или главный вектор)

 

 

то, согласно выше сформулированной теореме проекции этого вектора можно определить как:

Таким образом, задача об аналитическом сложении сил сводится к нахождению проекций вектора суммы R по формулам (2.6) с последующим определением его модуля:

Направление искомого вектора R в пространстве определяют направляющие косинусы:

где α, β, γ – углы, которые образует вектор R с положительными направлениями осей x, y, z соответственно.