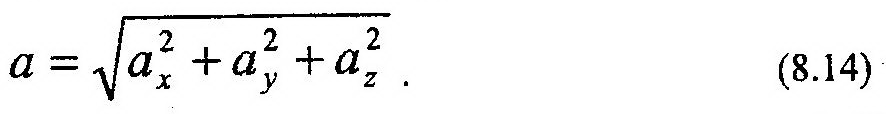Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия равновесия пространственной системы силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Аналитическая запись условий равновесия произвольной пространственной системы сил представляет систему шести уравнений (5.3).
С механической точки зрения первые три уравнения устанавливают отсутствие поступательного, а последние три − углового перемещения тела. В случае ССС условия равновесия будут представлены системой первых трех уравнений. В случае системы параллельных сил система будет состоять также из трех уравнений: из одного уравнения суммы проекций сил на ту ось, параллельно которой ориентированы силы системы, и двух уравнений моментов относительно осей, непараллельных линиям действия сил системы.
ЦЕНТР ТЯЖЕСТИ ТЕЛА Центром тяжести твердого тела называется точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела, при любом его расположении в пространстве. Координаты центра тяжести, точки C (рис. 6.3) можно определить по следующим формулам:
Ясно, что чем мельче разбиение, тем точнее будет проведен расчет по формулам (6.7), (6.8). Однако при этом трудоемкость вычислений может быть достаточно большой. В инженерной практике применяются формулы определения центра тяжести тел правильной формы.
КИНЕМАТИКА ЛЕКЦИЯ 6. Кинематикой называют раздел механики, в котором рассматривают движение тел и Точек без учета сил, приложенных к ним. 6.1. Способы задания движения точки Рассматривать движение тел или точек можно только относительно какой- либо системы отсчета – реального или условного тела, относительно которого определяют положение и движение других тел. Рассмотрим три, наиболее используемые при решении задач, системы отсчета и, соответствующие им, три способа задания движения точки. Их характеристика сводится к: а) описанию самой системы отсчета; б) определению положения точки в пространстве; в) указанию уравнений движения точки; г) установлению формул, по которым могут быть найдены кинематические характеристики движения точки. Векторный способ Данный способ используют, как правило, при выводе теорем и других теоретических положений. Его преимущество перед другими способами – компактность записи. В качестве системы отсчета в этом способе выступает центр О с тройкой единичных векторов – i, j, k (рис. 8.1). Положение в пространстве произвольной точки М определяется посредством радиуса-вектора, r. Таким образом, уравнением движения точки M будет однозначная функция радиуса-вектора от времени, t:
Сравнивая последние два определения, можно заключить, что траектория точки является одновременно годографом ее радиуса-вектора. Введем понятие средней скорости, Vср (рис. 8.1):
и истинной (мгновенной) скорости, V:
Направление V совпадает с касательной, к траектории точки (рис. 8.1). Ускорение точки – это векторная величина, характеризующая изменение скорости точки:
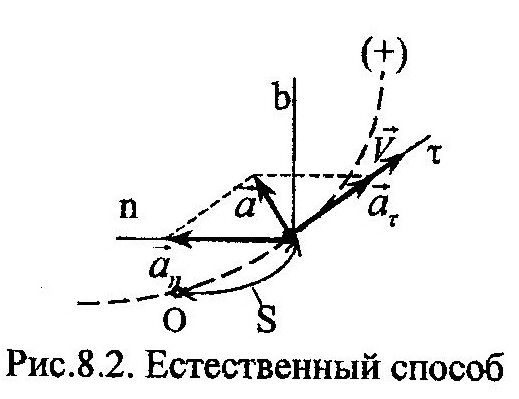
Естественный способ
ная зависимость между S и временем, t, представляет собой уравнение движения точки в естественном способе задания движения:
Скорость точки, направленная по оси t, определяется как:
Ускорение точки, а, находится в плоскости nt и может быть разложено на составляющие:
Физический смысл этого разложения заключается в следующем: линия действия касательной составляющей, аt, совпадает с линией действия вектора скорости, V, и отражает изменение только модуля скорости; нормальная составляющая ускорения, аn, характеризует изменение направления линии действия вектора скорости. Их численные значения могут быть найдены по следующим формулам:
Координатный способ Этот способ наиболее часто используют при решении задач. Системой отсчета является тройка взаимно перпендикулярных осей x, y, z (рис. 8.3). Положение точки М определяется ее координатами xМ, yМ, zМ. Уравнения движения точки представляют собой однозначные функции этих координат от
а ее модуль:
Направление вектора скорости в пространстве можно аналитически определить с помощью направляющих косинусов:
Ускорение точки М можно установить по его проекциям на координатные оси:
Направление вектора ускорения в пространстве определяется направляющими косинусами:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.27.78 (0.008 с.) |



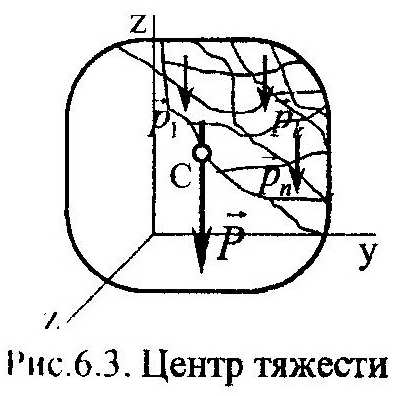
 где pk - вес элементарных частиц, на которое было разбито твердое тело.
где pk - вес элементарных частиц, на которое было разбито твердое тело.












 Составляющие скорости точки по осям равны:
Составляющие скорости точки по осям равны: