
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внешние силы. Определение внутренних сил методом сечения.Содержание книги
Поиск на нашем сайте
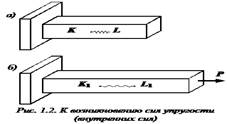
Внешние силы. Определение внутренних сил методом сечения. Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор (связей). Внешние силы делятся на объемные и поверхностные. Объемные силы приложены к каждой частице тела по всему его объему. Примером объемных сил являются силы веса и силы инерции. Часто задают простой закон изменения этих сил по объему. Объемные силы определяются их интенсивностью, как предел отношения равнодействующей сил в рассматриваемом элементарном объеме к величине этого объема, стремящего к нулю *1 и измеряются в Н/м3. Поверхностные силы делятся на сосредоточенные и распределенные. Определение внутренних сил, методом сечения. Метод сечений позволяет определить внутренние силы, которые возникают встержне, находящемся в равновесии под действием внешней нагрузки. Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Между этими частицами имеется некоторая пружинка, удерживающая их. Пусть натяжение пружинки равно нулю. Приложим теперь к стержню растягивающую силу Пусть в результате деформации стержня, частица K перейдет в положение К1, а частица L – в положение L1. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений. . Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить. Разрежем стержень, находящийся в равновесии под действием некоторой системы сил P. на две части плоскостью, перпендикулярной к его оси z. Отбросим одну из частей стержня и рассмотрим оставленную часть. Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами ______________________________________________________________________________
Напряжения. Основные понятия. Нормальные и касательные Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии)напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называютсянормальными HYPERLINK "http://www.sopromato.ru/rastyazhenie-i-szhatie/normalnie-napryazheniya-formula.html" напряжениями. Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии): *2 где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения. Правило знаков для нормального напряжения (*3), как и для продольной силы (N): при растяжении нормальное напряжение считается положительным, а при сжатии – отрицательным. http://sopromato.ru/pryamoy-izgib/epyuri-kasatelnih-napryazheniy-pryamougolnika-dvutavra-kruga.html 1.4 Растяжение и сжатие – это наиболее простые и часто встречающиеся виды деформации. На растяжение и сжатие работают многие элементы конструкций: стержни ферм, колонны, канаты лебедок, штоки паровых машин, лонжероны крыла самолетов. Растяжение и сжатие – это наиболее простые виды деформации, поэтому изучение курса сопромата начинается именно с изучения этих видовдеформации. Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжение (сжатие) вызывается внешними силами, действующими вдоль оси стержня z. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила (N), которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого сечения и направленных параллельно оси стержня. ______________________________________________________________________________
Деформации при растяжении и сжатии Деформация растяжения Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.
Посмотрите прибор измеряющий деформацию растяжения → Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен: 1. воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация) 2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация) 3. разрушаться на пределе прочности Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами. Деформация сжатия Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».
В качестве примера можно привести тот же прибор что и в деформации растяжения немного выше. Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры. Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности. _____________________________________________________________________________________ 1.6 Расчеты на прочность. Три задачи решаемые с помощью условия прочности.
Кручение Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил(момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор— крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию. Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения
где:
G — модуль сдвига. Отношение угла закручивания φ к длине
Деформация кручения является частным случаем деформации сдвига ГУКА ЗАКОН - основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (R. Hooke) в 1660. При растяжении стержня длиной l его удлинение При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи: а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку; б) проектировочный расчет - определить размеры вала из условия его прочности; в) расчет по несущей способности - определить максимально допустимый При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении: · по схеме вала и действующим на него скручивающим моментам строят · выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение · для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении
Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:
Для сплошного круглого сечения
Определив размеры вала из условия прочности, проверяют вал на жесткость по формуле
где Если данное условие не выполняется, то необходимо выбрать размеры вала из условия жесткости:
Учитывая, что для сплошного круглого сечения
Окончательно выбирают диаметр d, удовлетворяющий условиям прочности и жесткости.
Расчет на жесткость При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом т (рис. 27.4).
Произведение GJP называют жесткостью сечения. Модуль упругости можно определить как G Обычно рассчитывается угол закручивания, приходящийся на:дин метр длины бруса (вала) φо. Условие жесткости при кручении можно записать в виде
где φо — относительный угол закручивания, [φо] ≈ 1град/м = 0,02 рад/м - допускаемый относительный гол закручивания.
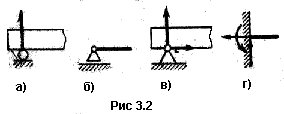
1.16 1.17 Изгиб Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб. Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом. Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов.
1. Подвижная шарнирная опора (рис. 3.2, а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка. Схематичное изображение подвижной шарнирной опоры дано на рис. 3.2, б. Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений. 2. Неподвижная шарнирная опора (рис. 3.2, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие - горизонтальную и вертикальную. 3. Жесткая заделка, или защемление (рис. 3.2, г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент). Балка с одним заделанным концом называется консольной балкой или просто консолью. Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения - уравнения перемещений.
Рассмотрим пример
1. Приравняем нулю сумму проекций на ось Х всех сил, действующих на балку: Sх=0, Ах=0. 2. То же, на ось У: Sу=0 Ау – Р1 – q·а3=0 Ау = Р1 + q·а3 = 20 + 20·2= 60 кН Вертикальная составляющая реакций в консольной балке равна сумме сил, приложенных к балке.
SМА=0 МА + Р1·2 + q· 2 · 5=0 МА = -Р1·2 - q· 10 = -20·2 - 20· 10= -240 кН ·м Знак (-) показывает, что направление момента следует изменить на обратное. Реактивный момент в заделке равен S моментов внешних сил относительно заделки.
При плоском поперечном изгибе в поперечных сечениях возникают два внутренних усилия М изгибающий и поперечная сила Q.
Отбросим одну из частей (правую) и рассмотрим равновесие левой части. Взаимодействие частей балки заменим внутренними усилиями: М изгибающий и поперечная сила Q. Для определения Мизг. и Q используем 2 уравнения равновесия: 1. Sу=0 Ау – Р1 + Q =0; Q = Р1 – Ау; Q = S (Рi) у 2. S М0 =0 Ах – Р1 (х –а1) + М = 0 М = Р1 (х –а1) – Ах; М = S т0 (Рi) Таким образом, поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения. Эпюры поперечных сил, изгибающих моментов. Общий порядок построения. 1. Определяем опорные реакции и делаем проверку. 2. Разбиваем балку на участки. За границы участков нагружения принимаем сечения, где приложены внешние силовые факторы, а также начало и конец распределенной нагрузки. 3. Применяя метод сечений, составим выражения для поперечных сил Q и изгибающих моментов Мизг. 4. По этим выражениям строим эпюры Q и Мизг., соблюдая правила знаков Q и Мизг. 5. На эпюре Q в месте приложения сосредоточенной нагрузки есть скачок равный этой силе, на эпюре Мизг скачок равен моменту, приложенному в данном сечении. I Σ Х = 0 RХА = 0 ΣУ = 0 RАУ + RВУ – 2Р = 0 RАУ + RВУ = 2Р RАУ = RВУ = Р Проверка: Σ МА = 0 RВУ · 4а – Р · 3А – РА = 0 0 = 0
II 3 участка нагружения III Метод сечений: Первое сечение Q = RА = Р Мизг = RАХ1; если Х1 - 0 → Второе сечение Мизг = 0; если Х1 = а → Мизг = Ра Q = RА - Р = Р – Р = 0 Мизг = RА · (а + х2 ) – РХ2 = РХ2 Ра – РХ2 = Ра Третье сечение Q = -RВ = - Р Мизг = RВ X3 = РХ3 Если Х3 = 0 → Мизг = 0 Если Х3 = а → Мизг = Ра
Деформация изгиба Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб. Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных центральных осей поперечного сечения стержня, изгиб называют простым или плоским (применяется также название: прямой изгиб). Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, изгиб называют косым. 1.19 Условие прочности Где [ Wx- осевой момент сопротивления Мх- изгибающий момент _____________________________________________________________________________________
В ПРИЛОЖЕНИЯХ Ударное действие нагрузки Колебания упругих систем
КОНЕЦ I РАЗДЕЛА РАЗДЕЛ II 2.1. Основные понятия и определения: Деталь -изделие, изготовленное без сборочных операций. Звено - детали, соединённые между собой неподвижно или с помощью упругих связей. Механизм -система материальных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения остальных. Кинематическая пара – два звена, соединённые друг с другом неподвижно. Машина – устройство, создаваемое человеком для использования законов природы, с целью облегчения умственного или физического труда. Кинематическая цепь – связанная система объектов, образующих между собой кинематические пары. План механизма и последовательность его построения При выборе масштаба рекомендуют придерживаться стандартных чертежных масштабов, а также рассуждений удобства подсчетов и наглядности изображения. Например, масштабу М1:1 отвечает масштабный коэффициент μl=0,001м/мм, масштабу М1:2 отвечает μl=0,002м/мм и т.п. Для построения планов механизма должны быть заданные размеры всех его звеньев, а если строится одно конкретное положение механизма и положение начального звена. Последовательность построения планов механизма: выбирают масштаб построения находят длины отрезков, которыми на чертеже будут изображаться звенья прежде всего, на чертеж наносят положение неподвижного звена (намечаются неподвижные точки механизма, наносятся, при наличии, неподвижные направляющие); вычеркивают заданное положение начального звена. Если строится n планов механизма, то находят начальные («мертвые», крайние) положения механизма и, соответственно, начального звена; лишь после этого вычеркивают группы Ассура в порядке их присоединения при образовании механизма. Кинематическое исследование механизма целесообразно начинать с построения ряда его последовательных положений, соответствующих полному циклу движения. Закон движения ведущего звена обычно бывает задан. Для построения траектории какой-либо точки находят ее положение на всех положениях механизма, а затем найденные точки соединяют плавной кривой
П о р я д о к п о с т р о е н и й:
1) Отделим от ведущего (начального) звена и стойки структурную группу 2-3; видим, что положения ее точек А и О1 заданы, следовательно, положение точки В может быть определено. 2) Определим на чертеже (рис. 8) взаимное расположение точек О и О1 стойки, отложив желательный по величине отрезок (ОО1) мм.
3) Масштаб плана механизма 4) Принимая точку О за вершину угла, откладываем заданный угол j в указанном на рис. 8 направлении и вычерчиваем кривошип в первом положении ОА1 с учетом масштаба, т.е. 5) Из точки О1 описываем дугу радиуса 6) Из точки А1, положение которой уже известно, делаем на дуге засечку радиусом 7) Соединив прямыми точки А1 и В1, В1 и О1, получим план механизма в заданном положении. Чтобы начертить траекторию точки К, расположенной на звене АВ, строим несколько последовательных планов механизма (см. рис. 8).
На каждом плане отмечаем точку Кi, где i - порядковый номер положения ведущего звена. Проводя через все отмеченные точки плавную кривую, получим искомую траекторию точки К (шатунную кривую). Из чертежа видим, что характер движения звеньев механизма различен, а именно: кривошип ОА вращается вокруг неподвижной точки О, коромысло О1В совершает качательное движение относительно неподвижной точки О1 и шатун АВ совершает сложное плоско-параллельное движение.
Классификация По форме профиля зубьев:эвольвентные;круговые (передача Новикова);циклоидальные. По типу зубьев:прямозубые;косозубые;шевронные;криволинейные;магнитные. По взаимному расположению осей валов:с параллельными осями (цилиндрические передачи с прямыми, косыми и шевронными зубьями);с пересекающимися осями — коническимиПо форме начальных поверхностей:цилиндрические;конические;глобоидные; По окружной скорости колёс:тихоходные;среднескоростные;быстроходные. По степени защищенности:открытые;закрытые. По относительному вращению колёс и расположению зубьев:внутреннее зацепление (вращение колёс в одном направлении);внешнее зацепление (вращение колёс в противоположном направлении). Основные параметры: Число зубьев шестерни — Соединение с натягом Соединение с натягом — технологическая операция получения условно разъёмного соединения, которое получается при вставлении одной детали (или части её) в отверстие другой детали при посадке с натягом. Обычно соединяют детали с цилиндрическими или коническими поверхностями, также эти поверхности могут быть эллиптическими, призматическими и пр. Для получения неподвижного соединения необходим натяг (положительная разность диаметров вала и отверстия). После сборки вал и отверстие благодаря упругим и пластическим деформациям принимают один размер. Сборка соединения с натягом производится запрессовкой или температурным деформированием. Эти соединения применяют для установки на валы зубчатых колес, колец подшипников качения и других деталей. Соединения с натягом также применяют для изготовления сложных составных деталей (коленчатые валы, составные зубчатые и червячные колеса и др.). Соединяемые детали могут быть изготовлены из одинаковых или разных материалов.
Достоинства соединений: достаточно простая технология получения соединения; хорошее центрирование соединяемых деталей; способность воспринимать значительные динамические нагрузки, удары, колебания.
Недостатки: большое рассеяние прочности соединения среди одной партии в связи с разбросом действительных размеров сопрягаемых поверхностей деталей в пределах их полей допусков и значений коэффициента трения; снижение усталостной прочности валов в зоне посадки вследствие концентрации напряжений; трудности неразрушающего контроля прочности соединения; сложность сборки и разборки при больших натягах и размерах соединяемых деталей; возможность повреждения посадочных поверхностей при разборке.
Различают следующие способы получения соединения с натягом:
Запрессовка — простейший способ, при наличии необходимого оборудования обеспечивающий возможность контроля за нагрузкой отдельного соединения путем измерения силы запрессовки. Однако при запрессовке существует опасность повреждения посадочных поверхностей, кроме того, снижается коэффициент трения (сцепления) из-за сглаживания микронеровностей на поверхности контакта.
Нагрев охватывающей детали — технологически отработанный способ, обеспечивающий высокий коэффициент трения (сцепления) и, как следствие, повышение нагрузочной способности соединения в 1,5 раза по сравнению с запрессовкой, так как отсутствует сглаживание микронеровностей на поверхности контакта. Однако контроль нагрузочной способности такого соединения затруднен.
Охлаждение охватываемой детали применяют для установки с натягом небольших деталей в крупные детали (корпуса машин, станины); по свойствам этот способ аналогичен нагреву охватывающей детали.
Гидрозапрессовка — нагнетание масла под давлением в зону контакта через сверления в валу, что значительно (в 10— 15 раз) снижает необходимую силу запрессовки и распрессовки иуменьшает опасность задира посадочных поверхностей; наиболее эффективен этот способ при больших диаметрах посадки и в соединениях по конической поверхности. 2.13. В ПРИЛОЖЕНИХ Планетарные механизмы. Кинематическое исследование. Формула Виллиса. Планетарная передача (дифференциальная передача) — механическая система, состоящая из нескольких планетарных зубчатых колёс, вращающихся вокруг центральной, солнечной, шестерни. Обычно планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую шестерню, имеющую внутреннее зацепление с планетарными шестернями. Основными элементами планетарной передачи можно считать следующие: • Солнечная шестерня: находится в центре; • Водило: жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней; • Кольцевая шестерня: внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями. Во время Второй мировой войны была разработана особая конструкция планетарной передачи, которая использовалась для привода небольших радаров. 2.15 Планетарные механизмы. Формула Виллиса однорядный планетарный механизм; двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением двухрядный планетарный механизм с двумя внешними зацеплениями; двухрядный планетарный механизм с двумя внутренними зацеплениями. Элементы планетарного механизма имеют специальные названия: зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным"; колесо с внутренними зубьями называют "короной" или "эпициклом"; колеса, оси которых подвижны, называют "сателлитами"; подвижное звено, на котором установлены сателлиты, называют "водилом". Звено водила принято обозначать не цифрой, а латинской буквой h. Формула Виллиса
2.16. Червя́чная переда́ча (зубчато-винтовая передача) — механическая передача, осуществляющаяся зацеплением червяка и сопряжённого с ним червячного колеса. Червяк представляет собой винт со специальной резьбой, в случае эвольвентного профиля колеса форма профиля резьбы близка ктрапецеидальной. На практике применяются однозаходные, двухзаходные и четырёхзаходные червяки. Червячное колесо представляет собой зубчатое колесо. В технологических целях червячное колесо, как правило, изготовляют составленным из двух материалов: венец — из дорогого антифрикционного материала (например, из бронзы), а сердечник — из более дешёвых и прочных сталей или чугунов. Входной и выходной валы передачи скрещиваются, обычно (но не всегда) под прямым углом Передача предназначена для существенного увеличения крутящего момента и, соответственно, уменьшения угловой скорости. Ведущим звеном является червяк. Червячная передача без смазки и вибрации обладает эффектом самоторможения и является необратимой: если приложить момент к ведомому звену (червячному колесу), из-за сил трения передача работать не будет. Передаточные отношения червячной передачи закладываются в пределах от 8 до 100, а в некоторых случаях — до 1000. Достоинства: • Плавность работы • Бесшумность • Большое передаточное отношение в одной паре, благодаря чему червячные редукторы с большим передаточным числом значительно более компактны и менее массивны, чем эквивалентные зубчатые • Самоторможение • Повышенная кинематическая точность • Недостатки: • Сравнительно низкий КПД (целесообразно применять при мощностях менее 100 кВт) • Большие потери на трение (тепловыделение) • Повышенный износ и склонность к заеданию • Повышенные требования к точности сборки, необходимость регулировки • Необходимость специальных мер по интенсификации теплоотвода Указанные недостатки обусловлены связанной с геометрией передачи невозможностью получения жидкостного трения.
Червяки различают по следующим признакам: • по форме поверхности, на которой образуется резьба • цилиндрические • глобоидные • по направлению линии витка • правые • левые • по числу заходов резьбы • однозаходные • многозаходные • по форме винтовой поверхности резьбы • с архимедовым профилем • с конволютным профилем • с эвольвентным профилем Зубчатые колёса различают по следующим признакам: • по профилю зуба • прямой — (контакт по точке, не нагруженные передачи) • вогнутый — «охватывающий» червяк (контакт по линии) • роликовый — зубы вырожденного сектора заменены на винтовой ролик • по типу зубчатого колеса • полное колесо (полный оборот, непрерывное вращение) • зубчатый сектор (поворот сектора от одного крайнего положения до другого) • вырожденный сектор (в паре с глобоидным червяком — рабочая длина сектора меньше рабочей длины червяка) • Червячная передача главным образом применяется в червячных редукторах. • Достаточно часто червячные передачи используются в системах регулировки и управления — самоторможение обеспечивает фиксацию положения, а большое передаточное отношение позволяет достичь высокой точности регулирования (управления) и(или) использовать низкомоментные двигатели. • Благодаря этим же характеристикам червячные передачи и червячные редукторы широко применяются в подъёмно-транспортных машинах и механизмах (например, лебёдках) • Часто в виде червячной пары изг
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3062; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.233.83 (0.011 с.) |





 — геометрический полярный момент инерции;
— геометрический полярный момент инерции; — длина стержня;
— длина стержня;
 пропорц. растягивающей силе F; в этом случае Г. з. имеет вид
пропорц. растягивающей силе F; в этом случае Г. з. имеет вид  , где
, где  - нормальное напряжение в поперечном сечении стержня,
- нормальное напряжение в поперечном сечении стержня,  - относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня
- относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня  пропорц. относительному удлинению:
пропорц. относительному удлинению: 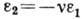 . Константа
. Константа  наз. коэф. Пуассона.
наз. коэф. Пуассона. ;
; (5.15)
(5.15) (5.16)
(5.16) , отсюда можем записать выражение для определения диаметра вала из условия его прочности:
, отсюда можем записать выражение для определения диаметра вала из условия его прочности: (5.17)
(5.17) , (5.18)
, (5.18) - допустимый относительный угол закручивания вала.
- допустимый относительный угол закручивания вала. (5.19)
(5.19) , можем записать выражение для определения диаметра вала из условия его жесткости:
, можем записать выражение для определения диаметра вала из условия его жесткости: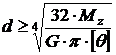 (5.20)
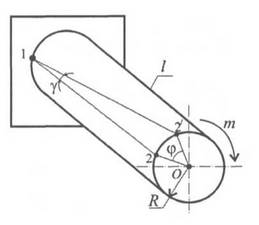
(5.20)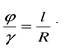 . Здесь φ - угол закручивания; γ – угол сдвига; l - длина бруса; R - радиус; R=d/2. Откуда
. Здесь φ - угол закручивания; γ – угол сдвига; l - длина бруса; R - радиус; R=d/2. Откуда 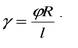 . Закон Гука имеет вид τk = Gγ. Подставим выражение для γ, получим
. Закон Гука имеет вид τk = Gγ. Подставим выражение для γ, получим 
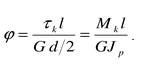 .
. 0,4Е. Для стали G = 0,8·105 МПа.
0,4Е. Для стали G = 0,8·105 МПа.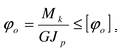 ,
, ;
;
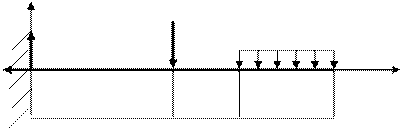
 Для их определения применим метод сечений. Сделаем мысленно разрез балки на расстоянии х от опоры А
Для их определения применим метод сечений. Сделаем мысленно разрез балки на расстоянии х от опоры А


 допускаемое нормальное напряжение при изгибе.
допускаемое нормальное напряжение при изгибе.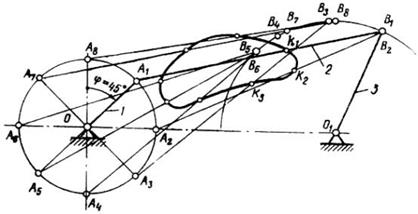
 ,где - длина стойки, м.
,где - длина стойки, м. ,где lОА - длина кривошипа, м.
,где lОА - длина кривошипа, м. .
. и отмечаем на ней точку В1.
и отмечаем на ней точку В1. ,Число зубьев колеса —
,Число зубьев колеса —  ,Модуль —
,Модуль —  ,Угол наклона линии зуба —
,Угол наклона линии зуба —  ,Передаточное отношение —
,Передаточное отношение — 




