
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжения при растяжении и сжатииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
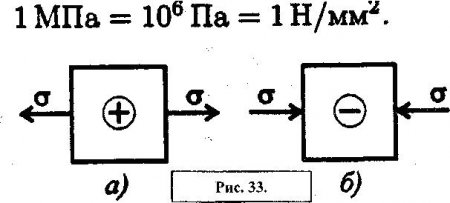
При растяжении и сжатии в сечении действует только нормальное напряжение.
Исходя из гипотезы плоских сечений, можно предположить, что напряжение при растяжении и сжатии в пределах каждого сечения не меняются. По этому напряжение можно рассчитать по формуле: где Nz - продольная сила; А - площадь поперечного сечения. Нормальные напряжения действуют при
Рис. 34.
Обнаруживаем три участка нагружения и определяем величины продольных сил. Участок 2: N2=2F. Строим эпюры продольных сил и нормальных напряжений.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское перпендикулярное оси, после деформаций остаётся плоским и перпендикулярным оси. 1.10 Cдвиг
Рис. 2.13. Деформация и напряжения при сдвиге
Срезу предшествует деформация – искажение прямого угла между двумя взаимно-перпендикулярными линиями. При этом на гранях выделенного элемента (рис. 2.13, в) возникают касательные напряжения. Величина
Используя ранее рассмотренный метод сечений, легко убедиться, что на боковых гранях выделенного элемента возникают только перерезывающие силы Q=F, являющиеся равнодействующими касательных напряжений:
Принимая во внимание, что касательные напряжения распределены равномерно по поперечному сечению А, их значение определяется соотношением:
Экспериментально установлено, что в пределах упругих деформаций величина касательных напряжений пропорциональна относительному сдвигу (закон Гука при сдвиге):
где G – модуль упругости при сдвиге (модуль упругости второго рода). Между модулями продольной упругости и сдвига существует взаимосвязь
где Приближенные значения модуля упругости при сдвиге, МПа: сталь – 0,8·105; чугун – 0,45·105; медь – 0,4·104; алюминий – 0,26·105; резина – 4.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.114 (0.008 с.) |




 смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол
смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол  , на который изменяются прямые углы элемента – относительный сдвиг:
, на который изменяются прямые углы элемента – относительный сдвиг: . (2.27)
. (2.27) . (2.28)
. (2.28) . (2.29)
. (2.29) , (2.30)
, (2.30)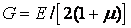 ,
,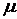 – коэффициент Пуассона.
– коэффициент Пуассона.


