Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений в грунте методом угловых точекСтр 1 из 3Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО
Кафедра оснований, фундаментов, динамики сооружений
МЕХАНИКА ГРУНТОВ Задания и методические указания к контрольной работе для студентов
Казань УДК 624.131 ББК 26.329
В методических указаниях даны задания, описания последовательности и примеры решения задач по МГ. Сост.: И.Т. Мирсаяпов, Д.Р. Сафин, Л.Ф.Сиразиев – Казань, КГАСУ, 2014. Предназначены для студентов заочной дистанционной формы обучения технических специальностей строительных вузов и составлены в соответствии с действующими стандартами и учебными программами.
© Казанский государственный архитектурно-
введение
Механика грунтов есть теория естественных грунтовых оснований. Роль механики грунтов как инженерной науки огромна, и ее можно сравнить с ролью дисциплины «Сопротивление материалов». Без знания основ механики грунтов не представляется возможным правильно запроектировать современные промышленные сооружения, жилые здания (особенно повышенной этажности), дорожные, земляные и гидротехнические сооружения. Применение основ механики грунтов позволяет полно использовать несущую способность грунтов, достаточно точно учесть деформации грунтовых оснований под действием нагрузки от сооружений, что обуславливает принятие не только наиболее безопасных, но и наиболее экономичных решений. Одновременно с изучением программного теоретического материала учебный план предусматривает практические занятия. Практические занятия являются одним из ответственных звеньев учебного процесса и имеют целью закрепить знания, полученные студентами за период изучения теоретического курса, а также должно способствовать умелому применению этих знаний при инженерном решении задач теории механики грунтов. В процессе выполнения контрольной работы студент должен научиться пользоваться действующими строительными нормами и правилами, руководствами, справочными и литературными материалами. В методические указания включены лишь некоторые из наиболее важных задач, позволяющие студентам на практике закрепить, систематизировать и более глубоко усвоить теоретические положения курса "Механика грунтов".
УКАЗАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ Исходные данные для решения задач выбираются студентом из таблиц 2.1 – 2.5 в соответствии с его личным учебным шифром (номером зачетной книжки). Шифром считаются последние две цифры номера зачетной книжки, если номер зачетной книжки – 06-92-1156, то учебным шифром будет 56. Первая и вторая цифры шифра используются для выбора исходных данных при решении задач. Работа оформляется в ученической тетради или на листах бумаги формата А4, которые следует сброшюровать. Работа пишется вручную, чертежи и эпюры напряжений строятся в карандаше. Получив после рецензирования контрольную работу, студент должен внести все указанные преподавателем исправления и дополнения. Исправления следует производить на том же листе (если позволяет место) или на отдельном и представить всю работу целиком на повторную рецензию. 2. задания к выполнению задач Задача №1. К горизонтальной поверхности массива грунта в одном створе приложены три вертикальные сосредоточенные силы Р1, Р2, Р3, расстояние между осями действия сил a и b. Определить величины вертикальных составляющих напряжений 2) по горизонтали II-II, проходящей на расстоянии h от поверхности массива грунта. Точки по вертикали расположить от поверхности на расстоянии 1,0, 2,0, 4,0, 6,0 м. Точки по горизонтали расположить вправо и влево от оси действия силы Р2 на расстоянии 0, 1,0, 3,0 м. По вычисленным напряжениям и заданным осям построить эпюры распределения напряжений Таблица 2.1.
Рис.2.1. Схема к расчету напряжений в грунте от совместного действия Задача №2. Горизонтальная поверхность массива грунта по прямоугольным плитам с размерами в плане Таблица 2.2.
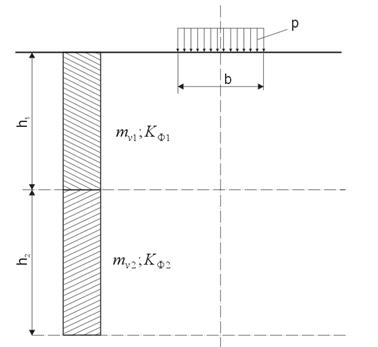
Рис.2.2. Схема к расчету напряжений в грунте методом угловых точек Задача№3. К горизонтальной поверхности массива грунта приложена вертикальная неравномерная нагрузка, распределенная в пределах гибкой полосы (ширина полосы Таблица 2.3
Рис.2.3. Схема к расчету напряжений в грунте от действия неравномерно Задача №4. Подпорная стенка высотой Н с абсолютно гладкими вертикальными гранями и горизонтальной поверхностью засыпки грунта за стенкой имеет заглубление фундамента а) грунт сыпучий; б) грунт сыпучий с пригрузом интенсивностью q, кПа;
в) грунт связный. Исходные данные приведены в таблице 2.4. Схема к расчету представлена на рисунке 2.4. Таблица 2.4
Рис.2.4. Схема к расчету подпорной стенки
Задача №5. Равномерно распределенная полосообразная (ширина полосы Таблица 2.5.
Рис.2.5. Схема к расчету методом послойного суммирования Задача №6. Равномерно распределенная в пределах прямоугольной площадки
Таблица 2.6.
Примечание. При определении значения коэффициента эквивалентного слоя
Рис.2.6. Схема к расчету методом эквивалентного слоя МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ. ПРИМЕРЫ РАСЧЕТА 3.1. Задача №1. Определение напряжений в грунте от действия
Для случая, когда к горизонтальной поверхности массива грунта приложено несколько сосредоточенных сил
где
Значения коэффициента При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Пример расчета Дано: Решение. Определяем напряжения в точках, расположенных по вертикали I-I. Точка 1 z=1 м. r1 =2 м r1/z=2/1=2 k1=0,0085 r2=0 r2/z=0/1=0 k2=0,4775 r3=3 м r3/z=3/1=3 k3=0,0015
Точка 2 z=2 м. r1 =2 м r1/z=2/2=1 k1=0,0844 r2=0 r2/z=0/2=0 k2=0,4775 r3=3 м r3/z=3/2=1,5 k3=0,0251
Точка 3 z=3 м. r1 =2 м r1/z=2/3=0,6667 k1=0,1889 r2=0 r2/z=0/3=0 k2=0,4775 r3=3 м r3/z=3/3=1 k3=0,0844
Точка 4 z=4 м. r1 =2 м r1/z=2/4=0,5 k1=0,2733 r2=0 r2/z=0/4=0 k2=0,4775 r3=3 м r3/z=3/4=0,75 k3=0,1565
Точка 5 z=6 м. r1 =2 м r1/z=2/6=0,33 k1=0,3687 r2=0 r2/z=0/6=0 k2=0,4775 r3=3 м r3/z=3/6=0,5 k3=0,2733
Определяем напряжения в точках расположенных по горизонтали II-II. Точка 6 z=3 м. r1 =1 м r1/z=1/3=0,33 k1=0,3687 r2=3 м r2/z=3/3=1 k2=0,0844 r3=6 м r3/z=6/3=2 k3=0,0085
Точка 7 z=3 м. r1 =1 м r1/z=1/3=0,33 k1=0,3687 r2=1 м r2/z=1/3=0,33 k2=0,3687 r3=4 м r3/z=4/3=1,33 k3=0,0374
Точка 8 z=3 м. r1 =3 м r1/z=3/3=1 k1=0,0844 r2=1 м r2/z=1/3=0,33 k2=0,3687 r3=2 м r3/z=2/3=0,67 k3=0,1889
Точка 9 z=3 м. r1 =5 м r1/z=5/3=1,67 k1=0,0171 r2=3 м r2/z=3/3=1 k2=0,0844 r3=0 r3/z=0/3=0 k3=0,4775
По полученным значениям напряжений строим эпюры распределения напряжений по соответствующим точкам (рис.3.1).
Рис. 3.1. Эпюры напряжений
Задача №2. Пример расчета Дано: Решение. Заданные плиты нагружения разбиваем на прямоугольники таким образом, чтобы они имели общую угловую точку, через которую проходит расчетная вертикаль М3 (рис. 2.2). Таким образом, имеем 5 прямоугольников: 1. 2. 3. 4. 5. Искомые напряжения найдем, суммируя напряжения от действия нагрузки по прямоугольникам 1, 2, 3 взятым со знаком «плюс» и напряжения от действия нагрузки по прямоугольникам 4, 5 со знаком «минус». z=1 м 1. 2. 3. 4. 5.
z=2 м 1. 2. 3. 4. 5.
z=4 м 1. 2. 3. 4. 5.
z=6 м 1. 2. 3. 4. 5.
По полученным значениям напряжений строим эпюру распределения напряжений
Рис.3.2. Эпюра напряжений Задача №3. Определение напряжений в грунте от действия
Для случая действия на поверхности массива грунта нагрузки, распределенной в пределах гибкой полосы по трапециевидной эпюре, величину вертикального сжимающего напряжения в заданной точке массива грунта определяют путем суммирования напряжений от прямоугольного и треугольного элементов эпюры внешней нагрузки. Вертикальные напряжения
где
Вертикальные напряжения
где Р – наибольшая ордината треугольной нагрузки. При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Пример расчета Дано: Решение. При расчете вертикальных напряжений равномерно распределенную нагрузку принимаем Вычисляем напряжения в расчетных точках: Точка 1 z=1м, y=3м, b=6м, z/b=1/6=0.17, y/b=3/6=0,5, kz=0,5. z/=1м, y/=6м, b=6м, z//b=1/6=0.17, y//b=6/6=1, k/z=0,448.
Точка 2 z=2м, y=3м, b=6м, z/b=2/6=0.33, y/b=3/6=0,5, kz=0,495. z/=2м, y/=6м, b=6м, z//b=2/6=0.33, y//b=6/6=1, k/z=0,401.
Т очка 3 z=4м, y=3м, b=6м, z/b=4/6=0.67, y/b=3/6=0,5, kz=0,46. z/=4м, y/=6м, b=6м, z//b=4/6=0.67, y//b=6/6=1, k/z=0,312.
Точка 4 z=6м, y=3м, b=6м, z/b=6/6=1, y/b=3/6=0,5, kz=0,41. z/=6м, y/=6м, b=6м, z//b=6/6=1, y//b=6/6=1, k/z=0,241.
Точка 5 z=4м, y=-3м, b=6м, z/b=4/6=0,67, y/b=-3/6=-0,5, kz=0,46. z/=4м, y/=0, b=6м, z//b=4/6=0.67, y//b=0/6=0, k/z=0,145.
Точка 6 z=4м, y=-1м, b=6м, z/b=4/6=0,67, y/b=-1/6=-0,17, kz=0,673. z/=4м, y/=2м, b=6м, z//b=4/6=0.67, y//b=2/6=0,33, k/z=0,287.
Точка 7 z=4м, y=0, b=6м, z/b=4/6=0,67, y/b=0/6=0, kz=0,717. z/=4м, y/=3м, b=6м, z//b=4/6=0.67, y//b=3/6=0,5, k/z=0,359.
Точка 8 z=4м, y=1м, b=6м, z/b=4/6=0,67, y/b=1/6=0,17, kz=0,673. z/=4м, y/=4м, b=6м, z//b=4/6=0.67, y//b=4/6=0,67, k/z=0,386.
По полученным значениям строим эпюры распределения напряжений (рис. 3.3).
Рис.3.3. Эпюры напряжений
Пример расчета Дано: Высота стенки H =6 м. Высота заглубления стенки h/ =1,5 м. Угол внутреннего трения грунта φ =160. Удельный вес грунта γ =22 кН/м3 Решение. Активное давление грунта на подпорную стенку:
Равнодействующая активного давления:
Пассивное давление грунта на подпорную стенку:
Равнодействующая пассивного давления:
По полученным данным строим расчетную схему и эпюру напряжений (рис.3.4.1). При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в 1 см.
Рис.3.4.1. Расчетная схема подпорной стены
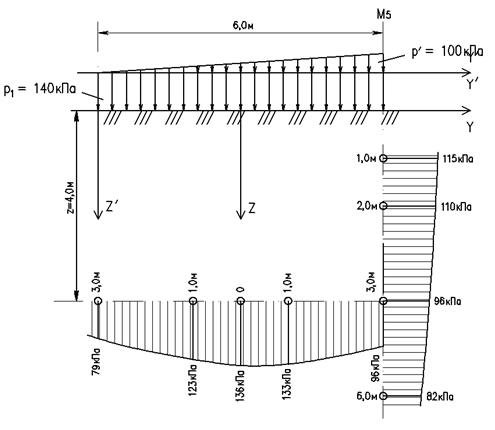
Пример расчета Высота стенки H =6 м. Высота заглубления стенки h/ =1,5 м. Угол внутреннего трения грунта φ =160. Удельный вес грунта γ =22 кН/м3. Интенсивность пригрузки Решение. Эквивалентная высота слоя грунта:
Активное давление на уровне верха подпорной стенки:
Активное давление на подошве подпорной стенки:
Равнодействующая активного давления:
По полученным данным строим расчетную схему и эпюру напряжений (рис.3.4.2). При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в 1 см.
Рис.3.4.2. Расчетная схема подпорной стены с пригрузом
Пример расчета Высота стенки H =6 м. Высота заглубления стенки h/ =1,5 м. Угол внутреннего трения грунта φ =210. Удельное сцепление грунта с =18 кПа. Удельный вес грунта γ =22 кН/м3. Решение: Действие сил сцепления заменяем всесторонним давлением связности:
Далее приводим вертикальное давление связности к эквивалентному слою грунта:
Активное давление на подошве подпорной стенки:
Равнодействующая активного давления:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2836; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.184 (0.272 с.) |
от совместного действия сосредоточенных сил в точках массива грунта, расположенных в плоскости действия сил: 1) по вертикали I-I, проходящей через точку приложения силы Р2;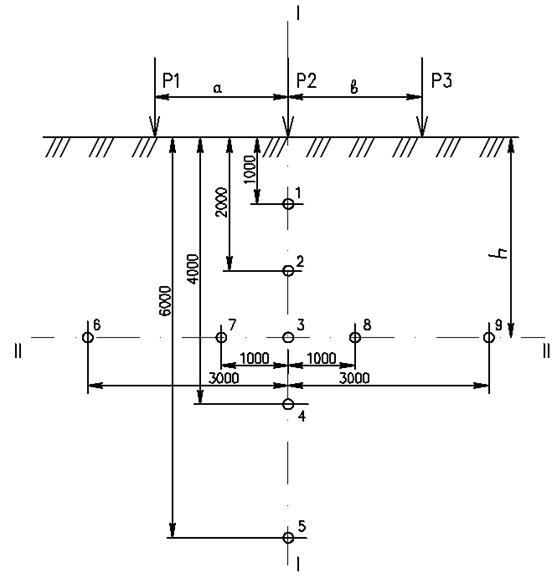
и 
нагружена равномерно распределенной вертикальной нагрузкой интенсивностью Р1 и Р2. Определить величины вертикальных составляющих напряжений 
от совместного действия внешних нагрузок в точках массива грунта для заданной вертикали, проходящей через одну из точек М1, М2, М3 на плите №1. Расстояние между осями плит нагружения L. Точки по вертикали расположить от поверхности на расстоянии 1,0, 2,0, 4,0, 6,0 м. По вычисленным напряжениям построить эпюру распределения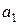 
, м
, м
, м
, м
, м
) по закону трапеции от Р1 до Р2. Определить величины вертикальных составляющих напряжений 
от поверхности. Точки по вертикали расположить от поверхности на расстоянии 1,0, 2,0, 4,0, 6,0 м. Точки по горизонтали расположить вправо и влево от середины загруженной полосы на расстоянии 0, 1,0, 3,0 м. По вычисленным напряжениям построить эпюры распределения напряжений 
. Определить активное и пассивное давление грунта на подпорную стенку при различных случаях загружения и грунтовых условиях:
,кН/м3
, град
, кПа
, кПа
приложена на глубине 
от горизонтальной поверхности слоистой толщи грунтов. Определить по методу послойного суммирования с учетом только осевых сжимающих напряжений величину полной стабилизированной осадки грунтов. С поверхности залегает песчаный грунт (мощность 
, плотность грунта 
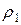, плотность частиц грунта 
, природная влажность 
, модуль общей деформации 
), подстилаемый водонепроницаемой глиной (
, 
, 
). Уровень грунтовых вод расположен в слое песчаного грунта на расстоянии 
от уровня подстилающего слоя. Исходные данные приведены в табл.2.5. Схема к расчету представлена на рис.2.5.
нагрузка интенсивностью 
, коэффициент фильтрации 
), подстилаемому глиной (
, 
). Определить по методу эквивалентного слоя величину полной стабилизированной осадки грунтов, изменение осадки грунтов во времени в условиях одномерной задачи теории фильтрационной консолидации, построить график стабилизации осадки вида 
. Исходные данные приведены в табл.2.6. Схема к расчету представлена на рис.2.6.
,
м
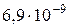
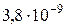
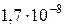
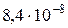
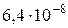
(для абсолютно жестких фундаментов), коэффициент относительной поперечной деформации для сжимаемой толщи грунтов можно принять 
.
, величины вертикальных составляющих напряжений 
, (3.1.1)
- коэффициент, являющийся функцией отношения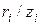 
;
- расстояние по горизонтальной оси от рассматриваемой точки до оси 
;
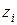- глубина рассматриваемой точки от плоскости приложения сосредоточенной силы 
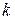приведены в табл.4.1 [2], табл.3.1 [5] или в таблице 1.1 приложения настоящих методических указаний.
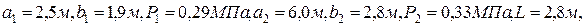расчетная вертикаль М3.
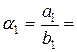2,5/1,9=1,32, 
1/1,9=0,53, 
0,2352.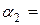
1,31, 
0,31, 
0,2457.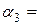
1,86, 
0,57,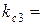 
0,232.
9,44, 
2,22, 
0,128.
3,89, 
2,22,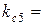 
0,1251.
1,32, 
1,06, 
, (3.3.1)
- коэффициент, определяемый в зависимости от величины относительных координат 
и 
, табл. 1.3 приложения 1 настоящих методических указаний;
, (3.3.2)
- коэффициент, определяемый в зависимости от величины относительных координат 
расчетная вертикаль М5.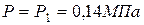
, при этом наибольшая ордината треугольной нагрузки 
. Начало координат для равномерно распределенной нагрузки находится в середине полосы нагружения, а начало координат для неравномерно распределенной нагрузки находится с краю полосы нагружения, где значение треугольной нагрузки равно нулю.
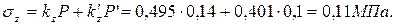
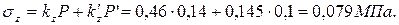
225 кН/м.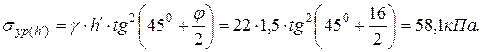
43,58 кН/м.
2,27м.
28,36кПа.
103,33 кПа.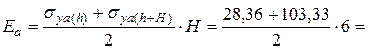
395,07 кН/м.
46,88 кПа.
2,13м.
38,0 кПа.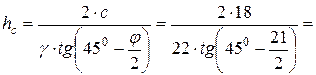
2,37 м.
