
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Гука. Пластичность . Упругость. ХрупкостьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёнымРобертом Гуком (Хуком) (англ. Robert Hooke)[1]. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности. В словесной форме закон звучит следующим образом: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации. Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения
Величина Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала. Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Упругость есть свойство материала изменять свою форму под нагрузкой и принимать ту же, первоначальную форму после ее удаления.
Пластичностью (вязкостью) называют способность материала под действием нагрузки изменять размеры и сохранять их после удаления нагрузки. При этом на материале не должна образовываться трещин. Свойство пластичности весьма широко используется при производстве и обработке строительных материалов (формование, ковка, прокатка, штампование изделий). К пластичным материалам, относится, например, арматурная сталь. Хрупкость — свойство материалов разрушаться внезапно без значительного изменения размеров и формы. К хрупким материалам относятся кирпич, бетон и др., которые легко разрушаются при ударах.
_____________________________________________________________________________________ Под механическими характеристиками подразумеваются значения напряжений и деформаций, соответствующие определенным точкам на диаграмме условных напряжений. Пределом пропорциональности σпц называется наибольшее напряжение, до которого деформации прямо пропорциональны напряжениям. Пределом упругости σу называется напряжение, до которого материал не получает остаточных деформаций. Пределом текучести σ т называется напряжение, при котором деформации растут без заметного увеличения нагрузки. Пределом прочности, или временным сопротивлением σв называется максимальное напряжение (подсчитанное по первоначальной площади сечения образца), выдерживаемое материалом при растяжении. Его величина определяется ординатой точки C условной диаграммы (см. Рис. 4.6). При экспериментальном определении величин пределов пропорциональности и упругости вносится определенный элемент условности. Объясняется это тем, что начало отклонения от линейной зависимости, как и начало образования остаточных деформаций, будет отмечено тем раньше, чем выше точность измерения деформаций. Поэтому под пределом пропорциональности σпц понимается напряжение, при котором отступление от линейной зависимости достигает определенной величины, устанавливаемой техническими условиями. Пределом упругости считается напряжение, при котором остаточные деформации достигают заранее установленной величины в пределах 0.001-0.005%. Условный предел упругости при остаточной деформации 0.005% обозначается σ0,005. Для материалов, не имеющих площадки текучести, в качестве предела текучести условно принимается напряжение, при котором остаточные деформации составляют 0.2 или 0.3% от первоначальной длины образца. Условный или, иначе, технический предел текучести в соответствии с допуском на остаточную деформацию обозначается σ0,2 или σ0,3. В теоретических исследованиях индексы 0.2 и 0.3 обычно опускаются и условный предел текучести обозначается символом σ т. Предел текучести является одной из основных характеристик материала. Пластические свойства материала, то есть способность к образованию остаточных деформаций, характеризуются величиной остаточного удлинения образца при разрыве
а также относительным уменьшением площади сечения образца в шейке
где l1, F1 - длина рабочей части образца и площадь наименьшего сечения шейки разорванного образца, соответственно; lo, Fo - их величины до нагружения. Основные механические характеристики применяемых в технике материалов приводятся в справочной литературе.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.119 (0.01 с.) |

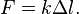
 — сила, которой растягивают (сжимают) стержень,
— сила, которой растягивают (сжимают) стержень,  — абсолютное удлинение (сжатие) стержня, а
— абсолютное удлинение (сжатие) стержня, а 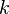 — коэффициент упругости (или жёсткости).
— коэффициент упругости (или жёсткости). и длины
и длины  ) явно, записав коэффициент упругости как
) явно, записав коэффициент упругости как
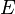 называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.



 ,
,
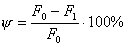 ,
,



