
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа, совершаемая внешними силами при вращательном движении относительно неподвижной осиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При вращательном движении системы вокруг неподвижной оси работу совершают внешние силы, действующие на систему. Каждая элементарная массаDmi в этом случае совершает вращательное движение в плоскости, перпендикулярной оси вращения. Траектория движения элементарной массы представляет собой окружность с центром на оси вращения. Работа силы F i по перемещению элементарной массы на элементарном пути d S i будет равна
где dSi = ridj; ri - радиус соответствующей окружности. Так как
Работа внешних сил, действующих на тело (систему) за время dt, будет вычислена так
Если проекция результирующего момента M на выбранное направление постоянна, то
7.2. Мощность Для оценки эффективности машин и механизмов важно знать, как быстро они совершают данную работу. Физическая величина, численно равная работе, совершаемой в единицу времени, называется мощностью. Таким образом, мощность характеризует работоспособность машин и механизмов. Различают мгновенную мощность и среднюю мощность. Средняя мощность - физическая величина, численно равная отношению работы, совершенной за некоторый промежуток времени Dt, к величине этого промежутка времени
Из формулы (7.16) видно, что если работа пропорциональна времени, A ~ Dt, то мощность постоянна. В большинстве случаев мощность зависит от времени N = f(t). В связи с этим вводится в рассмотрение понятие мгновенная мощность, которая определяется как первая производная от работы по времени: N = dA/dt. (7.17) Поскольку dA = F∙dS×cosa = (F ∙d S) = Fs×dS, (7.18) то N = d(F∙dS×cosa)/dt = d(F ∙d S)/dt = d(Fs×dS)/dt = F×v, (7.19) где F - мгновенная сила; v - мгновенная скорость. Таким образом, мгновенная мощность равна произведению мгновенной силы на мгновенную скорость. Формула (7.19) справедлива, когда сила F или скорость v постоянны. В этом случае N представляет собой постоянную мощность. При равномерно ускоренном движении (F = const) Nmax = F×vmax; <N> = F<v>. (7.20) При вращательном движении формулу для мгновенной мощности можно получить следующим образом: так как
то при ω2 = ω, ω1 = 0
Мгновенная мощность равна произведению мгновенного момента силы на мгновенную угловую скорость. Выражение (7.22) справедливо также и в том случае, когда M и w остаются постоянными, тогда мощность тоже постоянна. Если в формулу (7.22) подставить M = F∙r и w = v/r, то после сокращения получим N = Fv, (7.23) что совпадает с ранее полученной формулой (7.19). Для поступательного движения полученные соотношения можно использовать в том случае, когда Fi - тангенциальная сила, действующая на периферии тела, а v - скорость движения точки на периферии тела. В системе СИ мощность измеряется в ваттах (Вт). 7.3. Энергия как универсальная мера различных форм движений и взаимодействий В общем случае энергия выражает количественную меру и качественную характеристику движения и взаимодействия материи во всех ее превращениях. Понятие энергии связывает воедино все явления природы. В соответствии с различными формами движения материи рассматривают различные формы энергии: механическую, внутреннюю, электромагнитную, химическую, ядерную. Это деление до определенной степени условно. Так, химическая энергия складывается из кинетической энергии движения электронов и энергии взаимодействия электронов друг с другом и с атомными ядрами. Внутренняя энергия равна сумме кинетических энергий хаотического движения молекул и атомов относительно центра масс тел и потенциальной энергии взаимодействия молекул и атомов друг с другом. Энергия системы однозначно зависит от параметров, характеризующих состояние системы. В случае непрерывной среды или поля вводятся понятия плотности энергии, т.е. энергии в единице объема, и плотности потока энергии, равной произведению плотности энергии на скорость ее перемещения. Теория относительности показала, что энергия тела неразрывно связана с его массой m соотношением E = mc2. Любое тело обладает энергией. Если масса покоящегося тела m0, то его энергия покоя E0 = m0c2. Энергия может переходить в другие виды энергии при превращениях частиц (распадах, ядерных реакциях). Согласно классической физике энергия любой системы меняется непрерывно и может принимать любые значения. Квантовая теория утверждает, что энергия микрочастиц, движение которых происходит в ограниченном объеме пространства (например, электронов в атоме), принимает дискретный ряд значений. Так атомы испускают и поглощают электромагнитную энергию в виде дискретных порций - световых квантов, или фотонов. Оказывается, что любая материальная система может совершить лишь ограниченное количество работы, соответствующее определенному в данных условиях количеству присущего ей движения. Это свойство материальной системы совершать при переходе из данного состояния в некоторое другое определенную работу связано с ее энергией. Чем большую работу может совершить система при переходе в свое «нормальное» состояние, тем больше ее энергия в исходном состоянии. «Нормальным» состоянием системы называется такое ее состояние, в котором она уже не может совершать работу при данных условиях за счет энергии данного вида. Энергия может быть выражена через величины, характеризующие строение и свойства материальной системы. Она является функцией состояния системы, характеризует способность системы к совершению работы при переходе из одного состояния в другое. Разность энергий (изменение энергии), присущих системе в каких-либо состояниях, равна работе, совершаемой системой при переходе из одного состояния в другое: DW = W1 – W2 = A. (7.24) Механической энергией, соответствующей данной форме движения материи, называется величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи. Под механической энергией системы подразумевают сумму кинетической и потенциальной энергий. 7.4. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе При действии на движущееся тело постоянной по величине и совпадающей по направлению с направлением движения силы, тело либо приобретает определенный запас энергии, либо совершает работу. Физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки, называется кинетической энергией. Кинетическая энергия - энергия, которой обладает движущееся тело. Кинетическая энергия системы равна сумме кинетических энергий отдельных тел (материальных точек) этой системы: Wk = åWki, (7.25) где Wki - кинетическая энергия i-го тела системы. Изменение кинетической энергии системы при ее переходе из одного состояния в другое происходит под действием приложенных к системе внешних и внутренних сил и равно сумме работ этих сил: DWk = Wk2 – Wk1 = åAiвнут + åAiвн. (7.26) Уравнение (7.26) выражает теорему об изменении кинетической энергии, с помощью которой решаются многие задачи динамики. Изменение кинетической энергии системы равно сумме изменений кинетических энергий отдельных тел (материальных точек) системы:
Для вывода формулы кинетической энергии системы необходимо рассчитать работу, которая может быть совершена системой при ее торможении до полной остановки. Предположим, что система (твердое тело) состоит из n тел (материальных точек). При поступательном движении твердого тела со скоростью v каждая его материальная точка (элемент тела) движется с такой же скоростью. Элементарная работа сил трения при торможении, действующих на i-ю материальную точку, равна элементарному изменению кинетической энергии этой точки:
Изменение кинетической энергии материальной точки тела при переходе из одного состояния в другое имеет следующий вид:
Так как материальная точка и состояние тела были выбраны произвольно, то кинетическая энергия i-й материальной точки до начала торможения была следующей:
Это справедливо и в том случае, когда тело перемещается из точки
(7.31) Кинетическая энергия тела массой m равна сумме кинетических энергий отдельных материальных точек (частей) этого тела. В рассматриваемом случае
где m = åmi - масса тела (системы). Из формулы (7.32) видно, что кинетическая энергия не может быть отрицательной величиной, зависит только от массы движущихся тел и их скорости, но не зависит от того, каким образом данное тело достигло данной скорости. Таким образом, кинетическая энергия системы (тела) является функцией состояния ее движения. Так как p = mv, то
Соотношение (7.33) устанавливает связь между кинетической энергией тела (системы) и его импульсом. При скоростях, близких к скорости распространения света в вакууме, кинетическая энергия материальной точки
где m0 - масса покоящейся материальной точки (масса покоя); с - скорость распространения света в вакууме; m0 c2 = E0 - энергия покоя материальной точки. При малых скоростях (v<<c) соотношение (7.34) переходит в формулу (7.30). Так как dWk = dA, то при: 1) dA > 0 - работа совершается над системой – dWk > 0 - кинетическая энергия системы возрастает; 2) dA < 0 - работа совершается системой – dWk < 0 - кинетическая энергия системы убывает; 3) dA = 0 - если система не совершает работу или работа не совершается над системой – dWk = 0 - кинетическая энергия системы не изменяется. 7.5. Энергия системы, совершающей вращательное движение При вращательном движении твердого тела любая ее элементарная массаDmi имеет свою собственную линейную скорость vi, но одну и ту же угловую скорость, которая равна угловой скорости w тела. Кинетическая энергия такой элементарной массы
где vi = ωri. Подставив значение vi в (7.35) будем иметь
где Ii = Dmiri2 - момент инерции материальной точки относительно выбранной оси вращения. Кинетическая энергия тела равна сумме кинетических энергий отдельных материальных точек:
где Таким образом, кинетическая энергия тела, совершающего вращательное движение относительно неподвижной оси вращения, прямо пропорциональна квадрату угловой скорости тела и его моменту инерции. Так как M = I×e = I×(dw/dt), а j = w×dt, следовательно,
То есть работа внешних сил, действующих на вращающуюся относительно неподвижной оси материальную точку (тело, систему), равна изменению кинетической энергии:
7.6. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия и устойчивость системы Потенциальная энергия - физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе. Физический смысл имеет только понятие потенциальная энергия системы. Изменение конфигурации системы, взаимного расположения тел или частей одного и того же тела возможно при переходе системы из одного состояния в другое. При этом происходит изменение потенциальной энергии, которое не зависит: а) от начального значения потенциальной энергии; б) промежуточных состояний системы; в) пути перехода системы из состояния в состояние. Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком dWp = - dA. (7.40) За счет изменения энергии dWp совершается элементарная работа. Знание потенциальной энергии играет большую роль при определении условий устойчивости тел. Так как модулю dA = dWp = F×dx×cosa и при a = 0 dWp = F×dx, то
Известно, что в положении равновесия действующая на тело сила F = 0. Таким образом,
Это означает, что в положении равновесия потенциальная энергия Wp либо минимальна, либо максимальна. Возникающая при отклонении от положения равновесия сила направлена к положению равновесия, а, следовательно, при удалении от положения равновесия эта сила совершает отрицательную работу; потенциальная энергия тела (системы) при этом возрастает. Это означает, что в положении равновесия потенциальная энергия системы минимальна. Таким образом, признаками устойчивого равновесия (положения) являются
то есть минимум потенциальной энергии. Потенциальная энергия является более общей характеристикой воздействия тел или частиц друг на друга, приводящей к изменению состояния их движения.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1040; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.211.190 (0.011 с.) |

 , (7.12)
, (7.12) - численное значение момента силы
- численное значение момента силы  , а dj = w∙dt, то
, а dj = w∙dt, то . (7.13)
. (7.13) . (7.14)
. (7.14)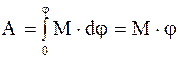 . (7.15)
. (7.15) . (7.16)
. (7.16) ., (7.21)
., (7.21)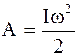 ,
, . (7.22)
. (7.22) ;
;  . (7.27)
. (7.27) .(7.28)
.(7.28) .
.  . (7.29)
. (7.29)
 . (7.30)
. (7.30) в точку
в точку  (рис.7.2). При этом совершается работа
(рис.7.2). При этом совершается работа  под действием силы
под действием силы  . Указанную работу можно представить следующим образом:
. Указанную работу можно представить следующим образом: .
. , (7.32)
, (7.32) . (7.33)
. (7.33) , (7.34)
, (7.34) , (7.35)
, (7.35)
 , (7.36)
, (7.36) , (7.37)
, (7.37) - момент инерции тела относительно той же оси вращения.
- момент инерции тела относительно той же оси вращения. . (7.38)
. (7.38) . (7.39)
. (7.39) . (7.41)
. (7.41) . (7.42)
. (7.42) > 0, (7.43)
> 0, (7.43)


