
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопоставление формул динамики поступательного движения и динамики вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лекция 4.Физика колебаний. Гармонический Дифференциальное уравнение гармонических колебаний и его решение. Модель гармонического осциллятора. Примеры гармонических осцилляторов: физический, математический и пружинный маятники. Определение их периодов и частот. Свободные колебания. Дифференциальное уравнение затухающих колебаний и его решение. Характеристики затухающих колебаний: коэффициент затухания, декремент, логарифмический декремент затухания, добротность. Вынужденные колебания гармонического осциллятора под действием синусоидальной силы. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс. Параметрический резонанс. 4.1. Дифференциальное уравнение гармонических колебаний и его решение Воспользовавшись основным уравнением классической динамики (уравнением второго закона Ньютона) можно получить уравнение движения материальной точки (тела), совершающего гармоническое колебание: F = m a или F = ma, (4.1) где a = d2x/dt2 = - ω02 x - ускорение материальной точки; F = å F i- результирующая сила, под действием которой совершается гармоническое колебание (возвращающая сила); F i - i-я сила, действующая на материальную точку. Тогда F = - mω02x = - kx, (4.2) где k = mω02 - коэффициент возвращающей силы, физический смысл которого заключается в том, что он численно равен возвращающей силе, вызывающей единичное смещение. Из уравнения (4.2) видно, что сила, под действием которой совершается гармоническое колебание, пропорциональна смещению и направлена в сторону противоположную ему. Она называется возвращающей силой. Возвращающая сила стремится вернуть материальную точку в положение равновесия. Возвращающие силы могут иметь различную природу. Например, они могут возникать за счет деформации. Силы, возникающие за счет упругой деформации, называются упругими. Силы, имеющие иную природу, - квазиупругими (как бы упругими). Таким образом, уравнение движения материальной точки при гармоническом колебательном движении имеет вид
С точки зрения математики уравнение (4.3) - однородное дифференциальное второго порядка, решением которого является выражение вида x = x0×sin(ω0t + φ0), (4.4) где x - смещение; x0 - амплитуда; ω0 - собственная (круговая или циклическая) частота; φ0 - начальная фаза. Решая дифференциальное уравнение гармонического колебательного движения, можно получить значение, например, периода колебаний, собственной частоты. 4.2. Примеры гармонических осцилляторов. Физический, математический и пружинный маятники. Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (4.3):
Колебания гармонического осциллятора являются примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. В качестве примеров гармонических осцилляторов рассмотрим гармонические колебания систем, называемых пружинным, физическим и математическим маятниками. Пружинный маятник Пружинный маятник - тело массой m, подвешенное на абсолютно упругой пружине, совершающее гармоническое колебание. Рассмотрим простую колебательную систему: верхний конец пружины зафиксирован, а нижний соединён с некоторым телом, имеющим массу
В действительности мы можем говорить лишь о преимущественном распределении параметров Направим вертикально вниз ось В данном случае действие силы тяжести не учитывается, т.к. оно приводит лишь к некоторому смещению тела из положения равновесия (точнее, к смещению самого положения равновесия) и никак не влияет на колебательный процесс. Беря проекцию силы упругости на ось
Разделив на
Решением дифференциального уравнения (4.6) является функция
В чем нетрудно убедиться, осуществив подстановку:
Параметр Решая дифференциальное уравнение, можно получить выражения для собственной частоты и периода колебаний пружинного маятника. Для чего в дифференциальное уравнение (уравнение движения пружинного маятника) необходимо подставить значения x = x0×sin(ω0t + φ0) и d2x/dt2 = - ω02x. Будем иметь - mω02x + kx = 0; - mω02 + k = 0, (4.7) откуда
Так как T = 2π/ω0, то для периода колебаний пружинного маятника получим
Надо отметить, что приведенное справедливо для упругих колебаний в пределах, в которых выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела. Анализируя колебательный процесс, мы приходим к выводу, что признаками колебательной системы являются следующие три: 1) положение равновесия, 2) возвращающая сила, 3) инерция.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.63.176 (0.009 с.) |

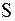 - Пройденный путь
- Пройденный путь
 - Угол поворота
- Угол поворота
 - Линейная скорость
- Линейная скорость
 - Угловая скорость
- Угловая скорость



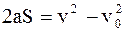
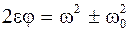
 - Mасса – мера инертности
- Mасса – мера инертности
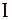 - Момент инерции относительно оси
- Момент инерции относительно оси
 - Cила
- Cила
 - Момент силы
- Момент силы

 .
.





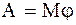




 или
или 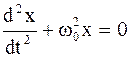 . (4.3)
. (4.3) . Мы рассматриваем колебательную систему с сосредоточенными параметрами
. Мы рассматриваем колебательную систему с сосредоточенными параметрами  , т.е. мы считаем, что масса сосредоточена в присоединённом теле, а упругость (жёсткость) характерна исключительно для пружины. На самом деле такое допущение – очередная абстракция, т.к. любая пружина имеет конечную (не нулевую) массу, а любое физическое тело обладает некоторой упругостью.
, т.е. мы считаем, что масса сосредоточена в присоединённом теле, а упругость (жёсткость) характерна исключительно для пружины. На самом деле такое допущение – очередная абстракция, т.к. любая пружина имеет конечную (не нулевую) массу, а любое физическое тело обладает некоторой упругостью. Рис.4.1
Рис.4.1
 , причем начало оси совместим с положением равновесия тела. При смещении тела из положения равновесия на него действует сила упругости
, причем начало оси совместим с положением равновесия тела. При смещении тела из положения равновесия на него действует сила упругости  . То есть в этом случае колебания возникают под действием сил упругой деформации F (возвращающей, упругой силы), пропорциональной деформацииDl = x.
. То есть в этом случае колебания возникают под действием сил упругой деформации F (возвращающей, упругой силы), пропорциональной деформацииDl = x.  или
или  , перепишем уравнение в следующем виде:
, перепишем уравнение в следующем виде: . (4.6)
. (4.6) , подстановка которой обращает уравнение в тождество. В данном случае решением является функция
, подстановка которой обращает уравнение в тождество. В данном случае решением является функция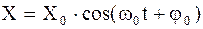 . (4.7)
. (4.7) ,
,  ;
;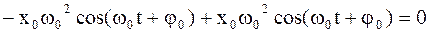 . (4.8)
. (4.8) называется собственной частотой свободных незатухающих колебаний. Таким образом, выведенная из равновесия система совершает незатухающие гармонические колебания с вполне определённой для неё частотой
называется собственной частотой свободных незатухающих колебаний. Таким образом, выведенная из равновесия система совершает незатухающие гармонические колебания с вполне определённой для неё частотой 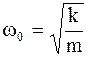 . (4.9)
. (4.9) . (4.10)
. (4.10)


