
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замедление хода движущихся часовСодержание книги
Поиск на нашем сайте
Cравним течение времени в различных инерциальных системах отсчёта. С этой целью воспользуемся часами – прибором, в котором используется тот или иной периодический процесс. Наиболее просто вопрос можно решить с помощью так называемых “световых” часов. Световые часы – это стержень с зеркалами на обоих концах, между которыми бегает короткий световой импульс. Период таких часов равен интервалу времени, в течение которого импульс проходит двойной путь от одного зеркала до другого (рис.9.4).
Каждый из наблюдателей, глядя на «свои» часы, констатирует, что их период одинаков. Но, глядя на «чужие» часы, которые находятся в относительном движении со скоростью Обозначим период движущихся часов
Так как 2l/c= Dt0, то
где v – скорость часов в неподвижной системе K. Отсюда видно, что Время, отсчитываемое по часам, движущимся вместе с телом, называется собственным временем этого тела Таким образом, в отличие от классической механики течение времени в действительности зависит от состояния движения. Не существует единого мирового времени, и понятие “промежуток времени между двумя данными событиями” оказывается относительным, поскольку зависит от выбора системы отсчета. Абсолютное время классической механики является в теории относительности приближенным понятием, справедливым только при малых (по сравнению со скоростью света) скоростях систем отсчета. Такой же результат можно получить, воспользовавшись преобразованиями Лоренца. Обозначим промежуток времени, прошедший между двумя событиями в системе К', Т0 = t2' - t1', в системе K - Т = t2 - t1. Запишим преобразования Лоренца:
Учитывая, что x1' = x2' (в системе К' часы покоятся), определяем Т, вычитая почленно из второго равенства первое:
Из формул (9.35) видно, что наименьшую длительность Т0 промежуток времени имеет в той системе отсчета, в которой оба события произошли в одной и той же точке пространства, в любой другой системе отсчета он будет иметь длительность тем большую, чем больше скорость v. Следует отметить, что речь идет не о каком-либо физически реальном изменении хода часов. Это связано с тем, что одна и та же пара событий разделена различными промежутками времени в разных системах отсчета. Для систем отсчета, движущихся со скоростью v<<c, промежуток времени между двумя событиями является приближенно абсолютной величиной. Поэтому в механике макроскопических тел и в обыденной жизни релятивистское замедление хода движущихся часов не играет никакой роли. В отличие от формулы сокращения длины (9.33) формула замедления времени (9.35) получила непосредственное экспериментальное подтверждение при изучении распада μ-мезонов, которые образуются в атмосфере Земли на небольших высотах под влиянием космических лучей. Они представляют собой частицы более тяжелые, чем электроны, но более легкие, чем протоны и нейтроны - масса их приблизительно равна 206 электронных масс. Эти частицы неустойчивые и распадаются за очень малый промежуток времени на электрон или позитрон (в зависимости от знака заряда μ-мезона) и две легкие нейтральные частицы нейтрино, т.е. эти частицы обладают малым временем жизни. С учетом этого они не должны были бы достигать поверхности Земли. Однако μ-мезоны обнаруживаются на поверхности Земли. Многочисленные опыты показывают, что в пределах экспериментальных ошибок соотношение Лекция 10. Релятивистская динамика Релятивистский импульс. Уравнение движения релятивистской частицы. Инвариантность уравнения движения относительно преобразований Лоренца. Работа и энергия. Полная энергия частицы. Четырехмерный вектор энергии-импульса частицы. Преобразования импульса и энергии. Закон сохранения четырехмерного вектора энергии и импульса. 10.1. Релятивистская масса и релятивистский импульс. Уравнение движения релятивистской частицы. Инвариантность уравнения движения относительно преобразований Лоренца. В классической динамике основными величинами являются: сила F - мера воздействия одного тела на другое (сила изменяет состояние движения, приводит к возникновению ускорения); масса m - индивидуальная постоянная, характеризующая инертность тела, т.е. степень его неподатливости сообщению ускорения; количество движения (импульс) p = m v - векторная величина, мера движения, указывающая на его направленность; кинетическая энергия Wк = =(mv2)/2 - скалярная величина, характеризующая движение только с количественной стороны. Между скоростью, силой, импульсом и кинетической энергией существует связь:
т.е. скорость изменения импульса тела равна действующей на тело силе (второй закон Ньютона), а скорость изменения кинетической энергии равна работе этой силы за единицу времени (мощности). Импульс и кинетическая энергия, как две меры движения, обладают существенными преимуществами по сравнению со скоростью, ускорением и т.п., так как для них имеют место так называемые законы сохранения. Кроме того, эти понятия являются распространенными и в других разделах физики. В классической динамике указывалось на то, что второй закон Ньютона в виде Причина в том, что масса движущихся тел зависит от их скорости движения. Кроме того, между массой всякого физического объекта и присущей ему (во взаимосвязи с окружающей средой) энергией W(E) имеет место, следующее соотношение: E = mc2, (10.2) где Е - полная энергия физической системы, включая энергию образующих ее частиц и полей; m - масса системы. На это со всей определенностью указывает опыт современной техники ускорения заряженных частиц микромира и экспериментальные подтверждения при многочисленных ядерных превращениях и фотоэлектрических явлениях. Эксперимент указывает на то, что при больших скоростях масса тела должна зависеть от абсолютной величины его скорости: m = m(v); Вид этой функциональной зависимости может быть однозначно установлен, если воспользоваться законом сохранения импульса и релятивистским законом сложения скоростей. Кроме того, его можно получить из следующих соображений. Так как для всех движений справедливо соотношение
то, учитывая, что dl/dt = v и d(mv) = m×dv + v×dm, имеем c2×dm = v2×dm + mv×dv. После разделения переменных получим
Интегрирование в пределах изменения скорости от 0 до v приводит к искомой зависимости в виде
где b = v/c; m - масса движущегося тела; m0 - масса покоя. Из выражения (10.4) видно, что с ростом скорости движения тела его масса увеличивается и при приближении скорости к скорости света в вакууме возрастает неограниченно. Согласно этой формуле масса тела - величина относительная, поскольку в разных системах отсчета скорость тела различна. Инвариантной величиной является только масса покоя m0. С учетом (10.4) запишем выражение для релятивистского импульса
Уравнение движения в релятивистской динамике (уравнение второго закона Ньютона) как закон изменения релятивистского импульса со временем имеет вид
Оно удовлетворяет требованиям принципа относительности, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы к другой и, следовательно, это уравнение инвариантно по отношению к преобразованиям Лоренца. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой. В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы в отсутствие внешних воздействий остается величиной постоянной. Уравнение (10.6) позволяет найти выражение для кинетической энергии тела. По определению приращение кинетической энергии равно работе силы:
С учетом того, что  , дифференцируя (10.7), найдем , дифференцируя (10.7), найдем
и, следовательно,
где B - постоянная интегрирования. При v = 0 Wk = 0, В = - m0×c2. Тогда кинетическая энергия тела, т.е. избыток энергии, которым обладает движущееся тело по сравнению с покоящимся телом, будет равна
Рассмотрим случай малых скоростей по сравнению со скоростью света в вакууме. Для чего разложим
Тогда выражение (10.10) для кинетической энергии примет вид
Из формулы (10.11) видно, что классическое выражение кинетической энергии Так, например, при скорости частицы v, составляющей 0,1 скорости света, второе слагаемое в (10.11) составляет 0,75% от первого, а при скорости v = 0,5 скорости света релятивистская кинетическая энергия, вычисленная по формуле (10.10), превышает классическое значение на 35%. При v®c кинетическая энергия тела неограниченно возрастает. Надо отметить, что масса покоя является мерой внутренней энергии в теле, а именно запас внутренней энергии в теле пропорционален массе покоя этого тела: Евн = m0×c2. (10.12) Полная энергия тела складывается из внутренней энергии и кинетической энергии тела как целого:
где Таким образом, масса тела является мерой запаса полной энергии тела. Всякое изменение энергии тела на величину DЕ влечет за собой изменение массы тела на Dm, причем
Уравнения 10.13 и 10.14 выражают один из важнейших законов современной физики - закон взаимной связи массы и энергии. Закон взаимной связи энергии и массы является универсальным законом - всякая материя (вещество в обычном смысле или излучение), обладающая энергией Е, обладает тем самым и массой m, равной E/c2. По аналогии с разделением полной энергии на внутреннюю энергию Евн и кинетическую Wк можно ввести деление релятивистской (полной) массы на массу покоя m0 и кинетическую массу mk, равную
Теория относительности, таким образом, внесла существенные изменения в понятие массы тела: масса тела, как характеристика его инертности, оказывается величиной не постоянной, как это считается в классической физике, а зависит от скорости: чем больше кинетическая энергия тела, тем больше и его масса. Кроме того, закон взаимной связи энергии и массы показывает, что масса зависит не только от энергии движения тела (от скорости), но и от запаса внутренней энергии. Это означает, например, что сжатая или растянутая пружина (напряженная пружина) имеет массу большую, чем ненапряженная пружина, что нагретое тело тяжелее холодного, намагниченный кусок железа тяжелее, чем не намагниченный. В отличие от классической физики в теории относительности существует общее выражение для запаса энергии тела, независимо от того, из каких видов энергии этот запас складывается (механическая, электромагнитная, внутриядерная и др.) - общая энергия тела или системы тел пропорциональна общей массе. Закон взаимной связи энергии и массы применяется для расчета энергии, выделяемой при ядерных превращениях. В классической и релятивистской физике в трактовке законов сохранения массы и энергии существует принципиальное отличие. В классической физике имеются два фундаментальных закона природы: 1) закон сохранения массы (закон сохранения вещества); 2) закон сохранения энергии. Согласно первому из этих законов, в замкнутой системе тел при любых физических и химических процессах масса системы остается неизменной: m = const. (10.16) Согласно второму закону, в замкнутой системе тел, находящейся в консервативном (независящем от времени) поле, при любых физических и химических процессах полная энергия системы остается величиной постоянной: E = const. (10.17) Эти два закона являются совершенно независимыми друг от друга, так как величина массы не определяет величину энергии, и наоборот. Более того, можно указать такие случаи, когда закон сохранения массы, с точки зрения классической физики, выполняется, а закон сохранения энергии нет (например, система зарядов в переменном электрическом поле). С точки зрения классической механики, масса является величиной аддитивной, т.е. масса системы равна сумме масс тел, составляющих эту систему. Поэтому закон сохранения массы в классической физике может быть сформулирован как закон сохранения суммы масс: в замкнутой системе тел сумма масс тел, вступающих в реакцию, равна сумме масс тел, возникающих в результате реакции:
В противоположность этому энергия не является величиной аддитивной: энергия системы тел не равна сумме энергий тел, составляющих эту систему, так как в общем случае существует еще энергия взаимодействия тел. Энергия системы тел выражается формулой
где величины Ei представляют собой энергии составных частей системы, а W - энергию их взаимодействия. В теории относительности существует единый закон сохранения энергии-массы. Действительно, поскольку между энергией и массой тела (системы тел) существует связь Однако содержание релятивистского закона сохранения массы значительно глубже, чем в классической физике. Прежде всего, масса системы согласно теории относительности не равна сумме масс составляющих ее тел. Действительно, из равенства
поделив обе части равенства на c2, получим
где m - масса системы; mi - масса изолированных тел, составляющих систему. Заметим, что масса системы может быть больше и меньше суммы масс, составляющих ее тел. Рассмотрим следующий практически важный случай. Пусть имеется устойчивая система частиц, обладающая известным запасом прочности (например, кристалл, атом, атомное ядро). Для того, чтобы разделить такую систему на составные части (разрушить кристаллическую решетку, т.е. расплавить или испарить кристалл; отделить электроны от атома; разделить ядро на протоны и нейтроны), необходимо совершить некоторую работу. Эта работа, очевидно, тратится на увеличение энергии частиц, составляющих систему. Поэтому сумма энергий разделенных частиц в этом случае больше энергии системы на величину энергии, которую принято называть энергией связи:
Поделив равенство (10.22) на c2, получим
Из формулы (10.23)видно, что сумма масс разделенных частиц больше массы системы на величину энергии связи, деленную на c2. Разность между суммой масс частиц и массой системы принято называть дефектом массы Dm. При этом
Видно, что чем прочнее система, чем больше ее энергия связи, тем больше дефект массы. Для химических соединений, обладающих сравнительно небольшой прочностью, энергия связи мала и дефекты масс оказываются далеко за пределами возможности экспериментального обнаружения. В ядерной физике дефект масс существенен, а следовательно, и велика энергия связи. Так, например, энергия связи ядра гелия в миллионы раз (»28 MeV) больше энергии связи химического соединения молекулы воды. Для того чтобы расщепить 1 г гелия на протоны и нейтроны, надо затратить энергию, равную 1,9×105 кВт∙час. Надо заметить, что из закона взаимосвязи энергии и массы не вытекает факт о возможности превращения массы в энергию, и наоборот. Например, часто утверждают, что при делении ядер урана часть его массы превращается в энергию. Это неправильное представление возникает в результате нечеткого понимания различия между массой покоя (с которой только и имеет дело классическая физика) и полной массой (понятием теории относительности). Следует подчеркнуть, что сразу после деления ядра урана полная масса его осколков в точности равна полной массе исходного ядра, так же, как и полная энергия его осколков равна полной энергии исходного ядра. В процессе деления происходит только частичное превращение массы покоя исходного ядра в кинетическую массу осколков и соответственно этому частичное превращение внутренней энергии исходного ядра в кинетическую энергию осколков. Известно, что в теории относительности, имеющей массу покоя m0 и движущейся со скоростью v,полная энергия частицы и ее импульс выражаются формулами
Воспользовавшись этими формулами, получим соотношение, связывающее полную энергию и импульс релятивистской частицы в векторной форме:
Исключив из этих формул скорость v, получим связь между импульсом и полной энергией в скалярной форме:
Связь между импульсом и кинетической энергией может быть представлена как
Формула (10.26) показывает, что для частиц с нулевой массой покоя энергия пропорциональна импульсу: E = c×p; p = E/c. (10.28) Кроме того, из (10.26), согласно теории относительности, существование частиц с нулевой массой, возможно, причем эти частицы должны обладать двумя важнейшими свойствами: 1) они должны двигаться со скоростью света в вакууме c; 2) их импульс и энергия должны быть связаны соотношением (10.28). Эти свойства сближают пока гипотетические частицы со световым излучением; как известно, излучение тоже распространяется в вакууме со скоростью c и обладает количеством движения (импульсом), связанным с энергией соотношением p = E/c. Это позволяет возродить на новых началах отброшенную в начале ΧΙΧ в. корпускулярную теорию света и рассматривать свет как поток корпускул с нулевой массой покоя. Эти частицы получили название световых квантов, или фотонов. Основные свойства фотонов: 1. Масса покоя фотонов равна нулю: m0 = 0. 2. Фотоны движутся со скоростью света в вакууме: v = c. 3. Поскольку энергия покоя фотонов равна нулю, их полная энергия равна кинетической энергии, причем она связана с импульсом фотона соотношением E = c×p. (10.29) 4. Не обладая массой покоя, фотоны обладают кинетической массой, которая равна полной массе:
Таким образом, фотоны обладают инертностью, причем эта инертность тем больше, чем больше энергия и импульс фотона. 5. Отсутствие у фотона массы покоя означает физически, что покоящиеся фотоны не существуют в природе. Прекращение движения фотона, остановка фотона. Означает его поглощение атомом. При этом масса фотона, энергия фотона и импульс фотона не исчезают, а передаются поглотившему атому. Поглощенный фотон исчезает как индивидуальная частица с соблюдением законов сохранения энергии и импульса. 10.2. Четырехмерное пространство - время. Преобразования в четырехмерном пространстве Основные понятия Известно, что в основе теории относительности лежит принцип относительности, согласно которому в физической системе, приведенной в состояние свободного равномерного и прямолинейного движения относительно системы, условно "покоящейся", для наблюдателя, движущегося вместе с системой, все процессы происходят точно так же, как в покоящейся системе. Этот факт формулируют в виде утверждения об инвариантности законов природы относительно преобразований движения. Термин "принцип относительности" связан с тем, что если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел останутся неизменными. Наряду с принципом относительности известны и другие принципы инвариантности, или симметрии, законов природы. Любой физический процесс происходит точно так же, если: а) осуществить его в любой другой точке пространства; б) систему, в которой происходит процесс, повернуть на произвольный угол; эта симметрия выражает равноправие всех направлений в пространстве, изотропию пространства; в) повторить процесс через некоторый произвольный промежуток времени; эта симметрия выражает однородность времени. Таким образом, имеет место инвариантность законов природы по отношению к четырем типам преобразований: 1) переносу в пространстве; 2) вращению в пространстве; 3) сдвигу во времени; 4) преобразованию движения. При этом преобразования (симметрии) выполняются точно только в изолированной от внешних воздействий системе, т.е. если можно пренебречь воздействием на систему внешних факторов; для реальных систем они справедливы только с определеной степенью точности. Изучение свойств первого и второго преобразований осуществляется в евклидовой геометрии трехмерного пространства, если рассматривать ее как физическую теорию, описывающую свойства физических объектов (при этом под переносом необходимо понимать преобразование параллельного переноса). При скоростях движения тел v, сравнимых со скоростью распространения света в вакууме c, обнаруживается тесная связь и математическая аналогия между преобразованиями 1,3 и 2,4. Это позволяет утверждать, что в теории относительности все преобразования следует рассматривать совместно. Содержанием специальной (частной) теории относительности является рассмотрение свойств указанных преобразований и следствий из соответствующих принципов инвариантности. Математически специальная теория относительности является обобщением геометрии Эвклида - геометрией четырехмерного пространства-времени (четырехмерной Минковского пространства-времени). Основное понятие теории относительности - точечное событие, т.е. нечто, происходящее в данной точке пространства в данный момент времени (например, выстрел, распад элементарной частицы). Это понятие является абстракцией - реальные события всегда имеют протяженность в пространстве и во времени и могут рассматриваться как точечные только приближенно. Любой физический процесс представляет собой последовательность событий (С): С1, С2, С3, …..,Сn. Справедливость преобразований (симметрий) 1-4 означает, что наряду с последовательностью (С) законы природы допускают существование последовательностей (С'), которые получаются из (С) соответствующим преобразованием и различаются положением событий в пространстве и во времени, но имеют одинаковую с (С) внутреннюю структуру. Например, в случае симметрии 4 можно наглядно описать процесс (С) как происходящий в стоящем на земле самолете, а процесс (С') как такой же процесс, происходящий в самолете, летящем с постоянной скоростью (относительно земли); различным скоростям и направлениям движения соответствуют различные последовательности (С'). Преобразования, переводящие одну последовательность событий в другую, называются активными (в отличие от пассивных преобразований, которые связывают координаты одного и того же события в двух системах координат). Совокупность всех возможных преобразований (1-4), с математической точки зрения, составляют группу, которая называется группой Пуанкаре. Преобразования группы Пуанкаре носят универсальный характер: они действуют на события любого типа. Это позволяет утверждать (считать), что они описывают свойства пространства-времени, а не свойства конкретных процессов. Преобразования Пуанкаре могут быть описаны различными способами (так же, как можно описать различными способами движения в трехмерном пространстве); наиболее простое описание получается при использовании инерциальных систем отсчета и связанных с ними часов. Роль инерциальных систем отсчета в теории относительности такая же, как роль прямоугольных координат в геометрии Эвклида. Под системой отсчета в этом случае можно подразумевать жёсткую систему твердых тел (или ее мысленное продолжение), по отношению к которой определяются положения событий, траектории тел и световых лучей. Любая система отсчета, движущаяся относительно данной инерциальной системы отсчета равномерно и прямолинейно, без вращения, также будет инерциальной, а система отсчета, вращающаяся или движущаяся ускоренно, не будет инерциальной системой отсчета. Таким образом, инерциальные системы отсчета образуют выделенный класс систем отсчета. Все инерциальные системы отсчета равноправны. Равноправие является непосредственным выражением принципа относительности. В области пространства-времени, в которой справедлива специальная теория относительности, можно пользоваться и неинерциальными системами отсчета (так же, как можно пользоваться криволинейными координатами в геометрии Эвклида), но при этом описание свойств пространства-времени оказывается более сложным.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.012 с.) |

 Далее представим себе две инерциальные системы отсчета K и K’, движущиеся относительно друг друга со скоростью v. Пусть и в той, и в другой системе имеются совершенно идентичные световые часы, жестко связанные с системой отсчета и ориентированные перпендикулярно вектору скорости v. Проследим теперь за ходом этих часов в обеих системах отсчета.
Далее представим себе две инерциальные системы отсчета K и K’, движущиеся относительно друг друга со скоростью v. Пусть и в той, и в другой системе имеются совершенно идентичные световые часы, жестко связанные с системой отсчета и ориентированные перпендикулярно вектору скорости v. Проследим теперь за ходом этих часов в обеих системах отсчета. , каждый заявит, что период у них будет больше. Например, наблюдатель, находящийся в системе K обнаружит, что световой импульс пройдет расстояние, равное удвоенной длине гипотенузы, т.е. большее, чем когда часы неподвижны. Причем это расстояние импульс проходит с той же скоростью, что и в неподвижной системе. Следовательно, часы в подвижной системе для этого наблюдателя будут идти медленнее.
, каждый заявит, что период у них будет больше. Например, наблюдатель, находящийся в системе K обнаружит, что световой импульс пройдет расстояние, равное удвоенной длине гипотенузы, т.е. большее, чем когда часы неподвижны. Причем это расстояние импульс проходит с той же скоростью, что и в неподвижной системе. Следовательно, часы в подвижной системе для этого наблюдателя будут идти медленнее. . Тогда из прямоугольного треугольника следует
. Тогда из прямоугольного треугольника следует  . Откуда
. Откуда .
. , (9.34)
, (9.34) ;
; , т.е. одни и те же часы, находящиеся в разных системах отсчета по отношению к данному наблюдателю, идут по-разному. Движущиеся часы идут медленнее, чем покоящиеся. Это явление называют замедлением времени.
, т.е. одни и те же часы, находящиеся в разных системах отсчета по отношению к данному наблюдателю, идут по-разному. Движущиеся часы идут медленнее, чем покоящиеся. Это явление называют замедлением времени. .
.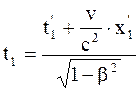 ;
;  .
. или
или  ;
;  . (9.35)
. (9.35) выполняется достаточно точно.
выполняется достаточно точно.
 , (10.1)
, (10.1) не применим в том случае, когда скорость движения тела (ее численное значение) стремится к численному значению скорости распространения света в вакууме, т.е. в релятивистских случаях. Оказывается, что второй закон Ньютона в данной форме не согласуется с принципом относительности СТО, не инвариантен по отношению к преобразованиям Лоренца и, следовательно, не может представлять собой точный закон природы, а является законом приближенным, справедливым только при малых скоростях движения тел.
не применим в том случае, когда скорость движения тела (ее численное значение) стремится к численному значению скорости распространения света в вакууме, т.е. в релятивистских случаях. Оказывается, что второй закон Ньютона в данной форме не согласуется с принципом относительности СТО, не инвариантен по отношению к преобразованиям Лоренца и, следовательно, не может представлять собой точный закон природы, а является законом приближенным, справедливым только при малых скоростях движения тел. . (10.3)
. (10.3) ,
, .
. , (10.4)
, (10.4) . (10.5)
. (10.5) Таким образом, в релятивистской динамике между импульсом тела и скоростью нет прямой пропорциональной зависимости, как в классической физике, а существует более сложная зависимость, выражаемая формулой (10.5) (рис.10.1).
Таким образом, в релятивистской динамике между импульсом тела и скоростью нет прямой пропорциональной зависимости, как в классической физике, а существует более сложная зависимость, выражаемая формулой (10.5) (рис.10.1). . (10.6)
. (10.6) . (10.7)
. (10.7)
 , (10.9)
, (10.9) . (10.10)
. (10.10) в ряд по степеням
в ряд по степеням  :
:
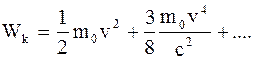 (10.11)
(10.11) представляет собой первое приближение к истинной величине Wk, справедливое лишь при малых скоростях.
представляет собой первое приближение к истинной величине Wk, справедливое лишь при малых скоростях. , (10.13)
, (10.13) - релятивистская масса.
- релятивистская масса. . (10.14)
. (10.14) . (10.15)
. (10.15) . (10.18)
. (10.18) , (10.19)
, (10.19) , то из закона сохранения массы для замкнутой системы (m = const) вытекает и закон сохранения энергии (E = const), и наоборот.
, то из закона сохранения массы для замкнутой системы (m = const) вытекает и закон сохранения энергии (E = const), и наоборот. , (10.21)
, (10.21) . (10.22)
. (10.22) . (10.23)
. (10.23) . (10.24)
. (10.24) ;
;  .
. . (10.25)
. (10.25) . (10.26)
. (10.26) . (10.27)
. (10.27) . (10.30)
. (10.30)


