
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика четырехмерного пространства-времениСодержание книги
Поиск на нашем сайте
Первый закон специальной теории относительности утверждает существование в природе систем отсчета сколь угодно близких инерциальным системам отсчета. При этом полагается, что не только механические, но и всякие другие явления выглядят в таких системах наиболее просто и описываются простыми уравнениями. Такими системами отсчета являются те, в которых свободное тело не имеет по отношению к ним ускорения. Второй закон Ньютона в специальной теории относительности формулируется так же, как и в классической механике, с помощью понятия импульса тела. При этом импульс тела представляется в четырехмерном пространстве-времени. Импульсом в четырехмерном пространстве-времени называют величину p = m0× v, (10.41) где m0 - масса тела в той системе отсчета, по отношению к которой тело покоится (масса покоя); v - скорость тела. Запишем это равенство в проекциях на соответствующие оси координат четырехмерной системы отсчета:
Так как
Первые три выражения в (10.43) - проекции обычного импульса на оси x, у и z в четырехмерной системе отсчета пространство-время. Уравнение движения материальной точки в четырехмерной системе отсчета пространство-время должно быть ковариантным по отношению к преобразованиям Лоренца, т.е. и справа, и слева должны быть векторы в четырехмерной системе отсчета пространство-время. Кроме того, слева должна стоять быстрота (скорость) изменения импульса, а справа сила. Так как изменение импульса за малое время dτ в рассматриваемой системе отсчета вектор d p = p - p 0, а время dτ для всех систем отсчета одно и то же, то d p /dτ - вектор, равный силе в четырехмерной системе отсчета пространство-время. Таким образом, уравнение движения материальной точки в четырехмерной системе отсчета пространство-время будет иметь вид
Заменив в (10.44) dτ на
Распишем уравнение (10.45) в проекциях на соответствующие оси координат четырехмерной системы отсчета пространство-время с учетом того, что p1 = px, p2 = pу, p3 =pz, p4 = imc:
В первых трех уравнениях формул 10.46 слева стоят производные от проекций импульса по обычному времени, т.е. по часам той системы, в которой скорость тела (материальной точки) равна v. Справа проекция обычной трехмерной силы:
Таким образом, проекции силы в четырехмерной системе отсчета отличаются от проекций силы в трехмерной системе координат множителем Для выяснения смысла четвертой проекции (10.46) определим скалярное произведение v на F:
или через проекции: v1×F1 + v2×F2 + v3×F3 + v4×F4 = 0. (10.49) Отсюда
Подставляя в правую часть равенства (10.50) вместо проекций векторов в четырехмерной системе отсчета пространство-время их выражения через проекции трехмерных векторов, получим
Подставляя полученное выражение для F4 в четвертую проекцию релятивистского уравнения движения (10.46), получим
Умножая (10.52) на ic, будем иметь
Но
Так как mc2 = E, то уравнение (10.54) можно записать в виде соотношения
Соотношение (10.55) выражает закон изменения энергии материальной точки в специальной теории относительности. Таким образом, релятивистские уравнение движения
Связь между трехмерным импульсом и энергией можно установить, если возвести в квадрат выражение
которое после соответствующих преобразований будет иметь вид
Так как mv = p, то
Умножая (10.58) на с2 и учитывая, что mc2 = E, получаем
вместо имевшегося в классической механике выражения
Уравнение (10.59) было получено ранее, но из других соображений. Можно показать, что из (10.59) при v2<<c2 вытекает (10.60). Надо отметить, что при v2<<c2 из формул релятивистской механики можно получить соответствующие формулы классической механики. Следует отметить, что работу dA = dE совершает результирующая сила f, а это означает, что величина
- это энергия, обусловленная движением тела, т.е. аналог кинетической энергии в классической механике. Частицу, не находящуюся в силовых полях (гравитационном, электрическом), называют свободной, а потому энергию E = mc2 часто называют энергией свободной частицы. 10.3. Столкновения релятивистских частиц. Законы сохранения энергии и импульса В специальной теории относительности оказывается справедливым и третий закон Ньютона: F μ,n = - F n,μ, (10.62) где F μ,n и F n,μ силы взаимодействия материальных точек в четырехмерной системе пространство-время, которые естественно отличаются (четвертой проекцией) от сил взаимодействия в трехмерном пространстве (в классической механике). Для системы материальных точек можно установить закон сохранения импульса в теории относительности (закон изменения релятивистского импульса). Имеем где p - релятивистский импульс; F -внешняя четырехмерная сила, действующая на систему. В случае замкнутой системы из N материальных точек, в отсутствие внешних воздействий, имеем d p = 0 или p = p 0, (10.63) то есть p = const, (10.64) где p и p 0 - импульсы после и до взаимодействия. Таким образом, в замкнутой системе материальных точек в отсутствии внешних воздействий релятивистский импульс сохраняется. Для компактной записи векторов в четырехмерной системе отсчета можно ввести орт l нормальный к обычным ортам i, j, k. Тогда любой вектор (например, B) в четырехмерной системе отсчета запишется в виде B = B1 i + B2 j + B3 k +B4 l, или B = b + B4 l, где b - трехмерная часть вектора B четырехмерной системы отсчета,а B4× l - его мнимая часть. С учетом сказанного векторы S, v, p запишутся в виде
В уравнениях (10.65) – (10.67) S, v, p - векторы четырехмерной системы отсчета пространство-время, а r, v ', p ' - их трехмерные составляющие. С учетом изложенного равенства (10.63, 10.64) можно записать так:
В формулах (10.68, 10.69) указано разное число частиц, так как при взаимодействии (ударе) могут образоваться новые частицы. Учитывая правила сравнения комплексных чисел, равенство (10.68) можно переписать в виде двух равенств
С учетом постоянства скорости света и l (10.71) запишется как
Равенство (10.70) отображает закон сохранения релятивистского импульса, а (10.72) - закон сохранения релятивистской массы (а значит, и энергии). Отметим, что формулы (10.62) – (10.72), строго говоря, справедливы лишь при взаимодействии материальных точек в одной и той же точке пространства. Если же материальные точки в пространстве-времени разделены, то (10.62) и Уравнение движения в компактной форме в теории относительности можно записать так:
С учетом того, что
получим
Равенство (10.73) - трехмерная часть закона движения в четырехмерной системе отсчета пространство-время или закон изменения трехмерной части импульса. Равенство (10.74) в проекции на орт l приводит, очевидно, к
что является законом изменения кинетической энергии. То, что равенство (10.62) описывает взаимодействие, происходящее в одной и той же точке пространства-времени (т.е. мгновенный удар при непосредственном контакте обеих материальных точек), следует из самого равенства (10.62). Именно, представляя силу F в виде двух слагаемых, получим
Но тогда (10.62) распадается на два равенства:
и
Эти два равенства не противоречат друг другу лишь при v m = v n, а это означает, что обе взаимодействующие материальные точки движутся совместно, т.е. их взаимодействие происходит в точке.
10.4. Значение теории относительности Специальная теория относительности, сменившая теорию, созданную Галилеем, Ньютоном и другими учеными имеет большое значение. Она: 1. Вывела физику из безвыходного положения с эфиром, нековариантностью уравнений по отношению к преобразованиям координат, связанных с переходом от одной системы к другой. 2. Установила границы применимости законов классической механики - они верны при движениях со скоростями, много меньшими скорости распространения света в вакууме. 3. Позволила глубже понять электромагнитные явления, в частности показала относительность понятий E и B. 4. Заставила пересмотреть представления о пространстве и времени. Оказалось, что понятия "размер", "форма" тела, "раньше", "позже" - относительные понятия. Метрические соотношения и промежутки времени в пространстве - относительны. Однако расстояния DS в четырехмерной системе отсчета пространство-время выражаются через приращения координат Dx1, Dx2, Dx3 и Dx4 так же, как и в трехмерной системе отсчета. То же самое можно сказать и про углы, линии, поверхности. Все геометрические соотношения, вся метрика в теории относительности такая же, как и в геометрии Эвклида на плоскости (только на таком плоском многообразии всего два измерения, два взаимно перпендикулярных направления, а в "мире" Минковского - четыре). В трехмерном пространстве свободное тело движется по прямой линии. Мировая линия такого тела в четырехмерной системе отсчета пространство-время - тоже прямая линия. Однако переход от четырехмерного многообразия Минковского (x1, x2, x3, x4) к реальному многообразию (x, у, z, t) приводит к тому, что квадрат пространственно-временного расстояния (квадрат интервала между двумя событиями) - не сумма квадратов приращений координат, а сумма-разность: DS2 = Dx2 + Dy2 Dz2 - c2Dt2. Из-за наличия знака "минус" в этой "теореме Пифагора" имеются существенные отличия геометрии теории относительности от геометрии классической физики. Поэтому геометрию теории относительности называют псевдоевклидовой (похожей на евклидову). 5. Установила совершенно неожиданные, с точки зрения классических представлений, связи между массой и энергией, массой покоя, энергией и импульсом. Нет ни одного факта или явления, противоречащего теории относительности. Подтверждениями этой теории являются:
1. Формула E = mc2, данная этой теорией, позволила использовать внутриядерную энергию. 2. Современные ускорители заряженных частиц строятся с учетом того, что для ускоряемых частиц 3. Некоторые элементарные частицы, например m-мезоны, по отношению к нашей системе отсчета (Земли) живут дольше, чем по "своим часам". Собственное время жизни m-мезонов порядка 10-8 с. Они проходят путь (через толщу атмосферы) порядка 105 м. Так как они не могут двигаться со скоростью, большей скорости распространения света в вакууме, то для прохождения такого расстояния им необходимо время Dt~0,3×10-2 с, что явно больше времени их жизни. Правда, живя по "своим часам" Dt'»10-8 с, они проходят путь не 105 м, а меньший, так как проходимое ими расстояние для них "сжимается". Таким образом, в системе отсчета, связанной с Землей, и в системе отсчета, связанной с мезоном, такие события, как вход мезона в атмосферу, достижение им поверхности Земли, оцениваются различными значениями Dt и Dt', Dr и Dr', как это следует из специальной теории относительности.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК Основной 1. Савельев И.В. Курс общей физики. М.: Наука, 1989. Т. 1, 2, 3. 2. Трофимова Т.И. Курс физики. М.: Высшая школа, 1995. 472 с. 3. Сивухин Д.В. Общий курс физики. М.: Наука, 1980. Т.1 - 6.
Дополнительный 1. Физика: Сборник контрольных заданий по механике для студентов инженерно-технических специальностей /Курск. гос. техн. ун-т. П.А. Красных, В.М. Пауков, В.М. Полунин, Г.Т. Сычёв; Под ред. В.М. Полунина. Курск, 1997. 93 с. 2. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1986. 208 с. 3. Сена Л.А. Единицы физических величин и их размерности. М.: Наука, 1977. 452 с.
Полунин Вячеслав Михайлович Сычев Геннадий Тимофеевич
ФИЗИКА Физические основы механики
Конспект лекций
Редактор О.А. Петрова Компьютерная верстка и макет А.А.Гончарова
Позиция плана № 35.2002
ИД № 06430 от 10.12.01 Подписано в печать. Формат 60х84 1/16. Печать офсетная. Усл. печ. л..Уч.-изд. л.. Тираж 250 экз. Заказ. Курский государственный технический книверситет Издательско–полиграфический центр Курского государственного технического университета: 305040, Курск, ул. 50 лет Октября,94
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.138.3 (0.012 с.) |

 ;
;  ;
; ;
; 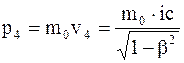 . (10.42)
. (10.42) , - масса движущейся материальной точки, то величины (10.42) проекций обычного импульса материальной точки в той системе отсчета, по отношению к которой ее скорость равна v
, - масса движущейся материальной точки, то величины (10.42) проекций обычного импульса материальной точки в той системе отсчета, по отношению к которой ее скорость равна v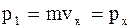 ;
;  ;
; ;
;  . (10.43)
. (10.43) . (10.44)
. (10.44) , получим
, получим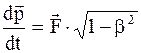 . (10.45)
. (10.45)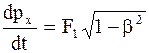 ;
;  ;
; ;
; 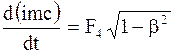 . (10.46)
. (10.46) ;
;  ;
; . (10.47)
. (10.47) , а первые три проекции релятивистского уравнения движения – это закон изменения трехмерного импульса, т.е. второй закон Ньютона, записанный в проекциях на оси x, у и z с учетом
, а первые три проекции релятивистского уравнения движения – это закон изменения трехмерного импульса, т.е. второй закон Ньютона, записанный в проекциях на оси x, у и z с учетом  .
. (10.48)
(10.48) . (10.50)
. (10.50) . (10.51)
. (10.51)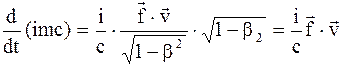 . (10.52)
. (10.52) . (10.53)
. (10.53) , следовательно:
, следовательно: . (10.54)
. (10.54) . (10.55)
. (10.55) . (10.56)
. (10.56) . (10.57)
. (10.57) . (10.58)
. (10.58) , (10.59)
, (10.59) . (10.60)
. (10.60) (10.61)
(10.61) (10.65)
(10.65) (10.66)
(10.66) (10.67)
(10.67) , (10.68)
, (10.68) . (10.69)
. (10.69) , (10.70)
, (10.70) . (10.71)
. (10.71) . (10.72)
. (10.72) , или
, или 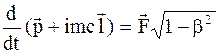 .
. и
и 
 , (10.73)
, (10.73) . (10.74)
. (10.74) ,
, . (10.75)
. (10.75) (10.76)
(10.76)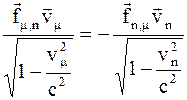 . (10.77)
. (10.77)


