
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика четырехмерного пространства-времениСодержание книги
Поиск на нашем сайте
Из постулатов теории относительности вытекает тот факт, что пространство и время образуют единую пространственно-временную четырехмерную систему отсчета (пространственно-временной континуум). Положение материальной точки, тела в ней может быть задано с помощью четырех координат: x, у, z, и t (x, у, z, - пространственные координаты; t - координата времени, равная t = ict, где В этом четырехмерном пространстве можно ввести четырехмерный радиус-вектор S = S (x1, x2, x3, x4). Смысл этого вектора состоит в том, что его три проекции на оси x1, x2 и x3 представляют собой обычные координаты материальной точки x, у и z в момент времени Если материальная точка за время Dt переместится на D r (на Dx, Dу, Dz), то в четырехмерном пространстве это отобразится четырехмерным перемещением D S,первые три проекции которого Dx, Dу, Dz (отображают перемещение материальной точки в обычном пространстве), а четвертая проекция, деленная на ic, будет равна Dt. Таким образом, введение четырехмерного пространства, четырехмерного радиус-вектора S и четырехмерного перемещения D S позволяет описывать протекание процессов в пространственно-временной системе отсчета. Известно, что расстояние между двумя точками в трехмерном пространстве определяется следующим соотношением:
В четырехмерном пространстве (в теории относительности) расстояние между двумя точками (событиями), которое называют пространственно-временным интервалом между двумя событиями, можно определить так:
Можно показать, что интервал между двумя событиями в пространственно-временной системе отсчета в случае распространения света равен нулю (DS = 0). Это позволяет утверждать, что интервал между двумя событиями в теории относительности инвариантен по отношению к переходу из одной системы отсчета в другую. При этом DS = DS', (DS)2 = (DS')2, (10.33) где DS и DS' - пространственно-временной интервал между двумя событиями в системах К и К' (система К' движется относительно системы К). Надо отметить, что DS = DS', а не D S = D S ', так как направления D S в разных системах отсчета различны, что и приводит к тому, что Dxi и Dxi' не равны. Дифференцируя пространственно-временной интервал по так называемому собственному времени движущегося тела t, в пространственно-временной системе координат можно ввести понятие скорости v и ускорения a. Интервал собственного времени di вводится следующим образом. Пусть некоторое тело в системе К имеет скорость v (обычная трехмерная скорость по отношению к системе К). За время dt по часам системы К это тело, двигаясь, переместится на d r (обычное трехмерное перемещение). Тогда пространственно-временной интервал будет иметь вид
Производя преобразования и учитывая, что
откуда
Так как в левой части равенства (10.35) стоят величины, не зависящие от выбора системы отсчета, то и правая часть равенства не зависит от выбора системы отсчета, т.е. является инвариантом перехода от одной инерциальной системы отсчета к другой. Эта величина имеет размерность времени и называется интервалом собственного времени движущегося тела, т.е. является промежутком времени dt, который отметят часы, находящиеся на теле, в то время как часы системы К, по отношению к которой тело движется со скоростью v, отметят время dt. Таким образом,
Скорость в четырехмерной системе отсчета
Чтобы уяснить смысл этой скорости запишем ее проекции:
Из (10.37) видно, что первые три проекции в Так как dS и dt для данного процесса не зависит от выбора системы отсчета, то и модуль скорости в четырехмерной системе отсчета не зависит от выбора системы отсчета, хотя модуль соответствующей ей скорости в трехмерной системе отсчета имеет разную величину в разных системах отсчета. Кроме того, величина скорости в четырехмерной системе одна и та же для всех тел и равна ic. Действительно, Ускорение в четырехмерной системе отсчета определяется формулой
Так как скорость v для всех тел постоянна, то v может меняться только по направлению, что означает в рассматриваемой четырехмерной системе отсчета a ^ v или a×v = 0, или в проекциях на оси a1×v1 + a2×v2 + a3×v3 + a4×v4 = 0. Очевидно, что по известному а (t) можно найти v (t) и S (t):
Следовательно, основные понятия и определения кинематики четырехмерного пространства-времени аналогичны основным понятиям и определениям кинематики классической механики. Отличие кинематики специальной теории относительности от кинематики материальной точки в классической механике заключается в следующем: 1. Специальная теория относительности имеет дело с векторами, описывающими поведение материальной точки в четырехмерном пространстве-времени. Классическая же кинематика имеет дело с векторами, описывающими поведение материальной точки в трехмерном пространстве. 2. То, что DS = DS', данное равенство вытекает из постулатов Эйнштейна. Для того чтобы v = v', необходимо их определить как отношение dS и dS' к такому времени dt, для которого имело бы место dt = dt', иначе при равных числителях и неравных знаменателях дроби dS/dτ и dS'/dτ' не были бы равны. Для этого и вводится в рассмотрение собственное время τ. По аналогичной причине и ускорение определяется как производная от скорости по собственному времени частицы τ. 3. Модули классических векторов r, v и dr имеютразличные значения в различных системах отсчета. Модули же векторов в четырехмерном пространстве-времени S,D S, v и другие для одной и той же мировой точки одинаковы во всех инерциальных системах отсчета. Иными словами, переход от системы К к системе К' сопровождается поворотом векторов S,D S, v, а и т.д., описывающих поведение мировой точки, на некоторые мнимые углы.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.186 (0.008 с.) |

 , c - скорость распространения света в вакууме, t - время). При этом x = x1, у = x2, z = x3, и t = ict = x4. По Минковскому, это четырехмерное пространство - "мир", в котором каждое мгновенное событие характеризуется точкой - мировой точкой с указанными координатами. События, происходящие с материальной точкой, отобразится в этом мире некоторой линией - мировой линией данной материальной точки (точнее, некоторой трубкой из-за протяженности тела).
, c - скорость распространения света в вакууме, t - время). При этом x = x1, у = x2, z = x3, и t = ict = x4. По Минковскому, это четырехмерное пространство - "мир", в котором каждое мгновенное событие характеризуется точкой - мировой точкой с указанными координатами. События, происходящие с материальной точкой, отобразится в этом мире некоторой линией - мировой линией данной материальной точки (точнее, некоторой трубкой из-за протяженности тела). , т.е. в момент времени, которым является четвертая проекция вектора S, деленная на ic.
, т.е. в момент времени, которым является четвертая проекция вектора S, деленная на ic. . (10.31)
. (10.31) . 0.32)
. 0.32) . (10.34)
. (10.34) , получим
, получим ,
, . (10.35)
. (10.35) . (10.36)
. (10.36) . (10.37)
. (10.37) ,
,  ,
, ,
, 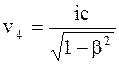 . (10.37)
. (10.37)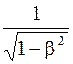 меньше проекций vx, vу и vz скорости v. Четвертая проекция - мнимая величина, не имеющая физического смысла.
меньше проекций vx, vу и vz скорости v. Четвертая проекция - мнимая величина, не имеющая физического смысла.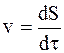 , а так как
, а так как  , то v = ic.
, то v = ic. . (10.38)
. (10.38) , (10.39)
, (10.39) . (10.40)
. (10.40)


