
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Физика волн. Волновые процессыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинематика и динамика волновых процессов. Плоская стационарная и синусоидальная волна. Интерференция и дифракция волн. Бегущие и стоячие волны. Фазовая скорость, длина волны, волновое число, волновой вектор. Упругие волны в газах, жидкостях и твердых телах. Энергетические характеристики упругих волн. Вектор Умова. 6.1. Кинематика и динамика волновых процессов. Волны – изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Процесс распространения колебаний в пространстве. Распространение колебаний в пространстве происходит благодаря взаимодействию между частицами упругой среды. Волна в отличие от колебаний характеризуется не только периодичностью во времени, но и периодичностью в пространстве. Частицы среды при этом не переносятся волной, они лишь совершают колебания около своих положений равновесия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества в пространстве. Среди разнообразия волн, встречающихся в природе и технике, выделяют упругие, на поверхности жидкости и электромагнитные. Упругими (или механическими) волнами называются механические возмущения, возникающие и распространяющиеся в упругой среде. К упругим волнам относятся звуковые и сейсмические волны; к электромагнитным – радиоволны, свет и рентгеновские лучи. В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные и поперечные волны. Продольные – это волны, направление распространения которых совпадает с направлением смещения (колебания) частиц среды. Поперечные – это волны, направление распространения которых и направление смещения (колебания) частиц среды взаимно перпендикулярны. В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому упругие деформации в них могут распространяться только в виде продольных волн (“волны сжатия”). В твердых телах, в которых упругие силы возникают при сдвиге, упругие деформации могут распространяться не только в виде продольных, но и в виде поперечных волн (“волны сдвига”). В твердых телах ограниченного размера (например, в стержнях и пластинах) картина распространения волны более сложна: здесь возникают еще и другие типы волн, являющиеся комбинацией первых двух основных типов. В электромагнитных волнах направления электрического и магнитного полей почти всегда перпендикулярны направлению распространения волны, (за исключением случаев анизотропных сред и распространения в несвободном пространстве) поэтому электромагнитные волны в свободном пространстве поперечны. Волны могут иметь различную форму. Одиночной волной, или импульсом, называется сравнительно короткое возмущение, не имеющее регулярного характера. Ограниченный ряд повторяющихся возмущений называется цугом волн. Гармоническая волна – бесконечная синусоидальная волна, в которой все изменения среды происходят по закону синуса или косинуса. Такие возмущения могут распространяться в однородной среде (если их амплитуда невелика) без искажения формы. Геометрическое место точек, до которых доходят волны за некоторый промежуток времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченного в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновых поверхностей существует бесконечное множество, в то время, как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными (они проходят через положения равновесия частиц, колеблющихся в одинаковой фазе). Волновой фронт все время перемещается. Волновые поверхности могут иметь различную геометрию. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, а в сферической волне - систему концентрических сферических поверхностей. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна расстоянию, на которое распространяется волна за один период:
где l - длина волны; T – период волны, т.е. время, за которое совершается один полный цикл колебания; n - частота, т.е. число периодов в единицу времени. Направление волны определяется с помощью волнового вектора k. Направление волнового вектора совпадает с направлением вектора скорости:
где w - круговая или циклическая частота. В акустике и оптике численное значение волнового вектора представляют в виде волнового числа:
6.2. Уравнение плоской волны Уравнение плоской волны - выражение, которое определяет смещение колеблющейся точки как функцию ее координат и времени, т.е.
x = x(x, у, z, t), (6.4)
где x - смещение. Эта функция должна быть периодической как относительно t, так и относительно x, у, z. Найдем вид функции
В точке пространства, расположенной на расстоянии x от места возникновения волны, частицы будут совершать те же колебания, что и в точке возникновения волны. Волновые поверхности в этом случае будут перпендикулярны к оси X. Поскольку все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от x и t x = x(x, t). Для прохождения расстояния от места возникновения до рассматриваемой точки волне требуется время. Фронт волны придет в рассматриваемую точку пространства спустя время Уравнение колебаний в рассматриваемой точке будет иметь вид
Формула (6.6) представляет собой уравнение прямой бегущей волны, т.е. распространяющейся в направлении положительной полуоси X. Бегущими волнами называются волны, которые переносят в пространстве энергию. Количественно перенос энергии волнами характеризуется вектором плотности потока энергии
Вектор плотности потока энергии – физическая величина, модуль которой равен энергии DE, переносимой волной за единицу времени (Dt=1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^). Направление вектора потока плотности энергии (вектора Умова) совпадает с направлением переноса энергии. Можно показать, что численное значение вектора потока плотности энергии определяется соотношением j = u×v, (6.8) где u – плотность энергии в каждой точке среды, среднее значение которой равно:
ρ – плотность среды; x0 – амплитуда волны; w - круговая (циклическая частота); v – фазовая скорость (скорость перемещения фазы волны). В векторной форме: j = u× v. (6.9) Фазовая скорость упругих волн: а) продольных б) поперечных где E – модуль Юнга (характеристика упругих свойств среды, обратная коэффициенту упругости); G – модуль сдвига (он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равен 45о, если бы при столь больших деформациях не был превзойден предел упругости). Понятие фазовой скорости справедливо для монохроматических волн. Так как распространяющиеся в пространстве волны представляют собой волновой пакет (в силу принципа суперпозиции), то кроме фазовой скорости, для волнового пакета вводят в рассмотрение понятие групповой скорости. Волновой пакет – совокупность волн, частоты которых мало отличаются друг от друга. Групповой скоростью называют скорость перемещения в пространстве амплитуды волны. С ней происходит перенос энергии волны. Групповая скорость определяется следующим соотношением:
Уравнение обратной волны можно получить путем замены в (6.6) х на (-х):
6.3.Волновое уравнение Оказывается, что уравнение любой волны является решением некоторого дифференциального уравнения второго порядка, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от уравнения волны: Производные по х:
Производные по t:
Разделим обе части уравнения (6.15) на v2:
Сравнивая выражения (6.14) и (6.16), убеждаемся в равенстве их правых частей, поэтому можем приравнять левые части этих уравнений:
Соотношение (6.17) является волновым уравнением плоской волны, распространяющейся вдоль оси X. Волновое уравнение плоской волны, распространяющейся в трехмерном пространстве, имеет вид
В математике вводят специальный оператор, называемый оператором Лапласа:
С применением оператора Лапласа /лапласиана/ волновое уравнение (6.17) принимает вид
Если при анализе какого-либо процесса, получают уравнение вида (6.19), то это означает, что рассматриваемый процесс - волна, распространяющаяся со скоростью v. 6.4. Интерференция волн. Стоячие волны При одновременном распространении в среде нескольких волн частицы среды совершают колебание, являющееся результатом геометрического сложения колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны накладываются одна на другую, не изменяя друг друга. Это явление называют принципом суперпозиции волн. В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают разностью фаз и имеют одинаковую частоту, волны называются когерентными. Когерентные волны излучаются когерентными источниками. Когерентными источниками называют точечные источники, размерами которых можно пренебречь, излучающие в пространство волны с постоянной разностью фаз. При сложении когерентных волн возникает явление интерференции. Интерференция – это явление наложения когерентных волн, в результате которого происходит перераспределение энергии волны в пространстве. Возникает интерференционная картина, заключающаяся в том, что колебания в одних точках усиливают, а в других - ослабляют друг друга. Наиболее часто интерференция возникает при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающая в результате такой интерференции волна называется стоячей. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и встречная - отраженная, складываясь, образуют стоячую волну. Пусть вдоль оси X распространяются прямая и обратная плоские волны, уравнения которых имеют вид
В данном случае результирующее колебание получается путем алгебраического сложения:
Воспользовавшись тригонометрическим тождеством
перепишем (6.22) в виде
Выражение (6.23) - уравнение стоячей волны. Амплитуда стоячей волны
Из (6.24) видно, что амплитуда, зависящая от x, может достигать максимального и минимального значений. Действительно: 1) при kx = ± np (n = 0, 1, 2, ¼) амплитуда максимальна: A = 2x0. Точки, в которых амплитуда смещения удваивается, называются пучностями стоячей волны; 2) при kx = ± (2n + 1)p амплитуда обращается в нуль. Эти точки называются узлами стоячей волны. Расстояние между соседними (узлам) – длина стоячей волны l0. Длина стоячей волны
Таким образом, длина стоячей волны равна половине длины бегущей волны. Графически стоячая волна выглядит так, как показано на рис.6.2. В соседних полуволнах колебания частиц имеют противоположную фазу, или, как говорят, сдвиг по фазе составляет p. В отличие от бегущей волны в пределах одной полуволны колебания всех точек происходят в одной и той же фазе, но с различной амплитудой. Очень часто стоячие волны используют для определения скорости распространения волн. Это достигается с помощью так называемого интерферометра.
В звуковом интерферометре источником звука (источником волны) является мембрана или пьезоэлектрическая пластинка - 1 (рис.6.3). Имеется отражатель (рефлектор) - 2. Перемещая рефлектор, получают систему стоячих звуковых волн. Если при перемещении рефлектора на расстояние L возникло n узлов, то скорость распространения звука будет равна
То есть для определения скорости распространения волны (звуковой волны) необходимо измерить длину стоячей волны l0 и частоту звуковых колебаний. Лекция 7. Энергия, работа, мощность Работа силы и её выражение через криволинейный интеграл. Мощность. Энергия как универсальная мера различных форм движений и взаимодействий. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе. Энергия системы, совершающей вращательное движение. Энергия системы, совершающей колебательное движение. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия тела, находящегося в поле тяготения другого тела. Потенциальная энергия и устойчивость системы. Внутренняя энергия. Энергия упругой деформации. 7.1. Работа силы и её выражение через криволинейный интеграл Работа - это изменение формы движения, рассматриваемое с его количественной стороны. В общем смысле работа - это процесс превращения одних форм движения материи в другие и одновременно количественная характеристика этого процесса. Механическая работа - процесс, в котором под действием сил изменяется энергия системы, и одновременно количественная мера этого изменения. При совершении работы всегда имеются сила, действующая на материальную точку (систему, тело), и вызванное данной силой перемещение. При отсутствии хотя бы одного из этих факторов работа не совершается. Элементарная работа некоторой силы F, действующей на материальную точку (тело, систему), вызывающей элементарное перемещение d r, равна произведению силы на перемещение: dA = F ×d r = F×dr×cosa = Fr×dr, (7.1) где α - угол между направлением перемещения и направлением действующей силы. Из (7.1) следует, что при α < π/2, dA > 0 - работа положительная; α = π/2, dA = 0 - работа не совершается; α > π/2, dA < 0 - работа отрицательная; α = 0, dA = F×dr - направление перемещения и направление действующей силы совпадают. В том случае, когда величина тангенциальной составляющей силы остаётся всё время неизменной, то работа определяется соотношением
В частности, это условие выполняется, если тело движется прямолинейно, и постоянная по величине сила
Надо отметить, что понятие работы в механике существенно отличается от обыденного представления о работе. Например, для того, чтобы держать тяжелый груз, стоя неподвижно, а тем более для того, чтобы перенести этот груз по горизонтальному пути, носильщик затрачивает определенные усилия, т.е. "совершает работу". Однако работа как механическая величина в этих случаях равна нулю. Вектор силы на плоскости всегда можно разложить на две составляющие - нормальную и тангенциальную. Ясно, что только тангенциальная составляющая силы способна совершить работу. В случае, когда величина проекции силы на направление перемещения не остается постоянной во времени, для вычисления работы следует разбить путь S на элементарные участки
А работа на всем пути S может быть вычислена как сумма элементарных работ:
В общем случае, когда материальная точка (тело, система), двигаясь по криволинейной траектории, проходит путь конечной длины, можно мысленно разбить этот путь на бесконечно малые элементы, на каждом из которых сила F может считаться постоянной, а элементарная работа может быть вычислена по формуле (7.1). Сложив все эти элементарные работы и перейти к пределу, устремив к нулю длины всех элементарных перемещений, а их число – к бесконечности, получим
Выражение (7.6) называют криволинейным интегралом вектора F вдоль траектории L.
Работу, определяемую формулой (7.6), можно изобразить графически, в координатах F - S, площадью фигуры, что соответствует нахождению криволинейного интеграла. На рис.7.1 построен график Ft как функции положения точки на траектории. Из рисунка видно, что элементарная работа Единица измерения работы в СИ носит название джоуль (Дж). Найдем работу, совершаемую при растяжении пружины, подчиняющемуся закону Гука. Сила, растягивающая пружину, равна по величине и противоположна по направлению упругой силе, т.е.
где Сила действует в направлении перемещения, поэтому
Элементарная работа в данном случае может быть представлена в виде
По формуле (7.6) найдем полную работу:
При сжатии пружины на величину Экспериментально установлено, что работа сил тяжести, упругих сил, электрических сил не зависит от формы траектории, а определяется начальным и конечным положениями материальной точки (системы, тела). Работа этих сил по замкнутой траектории равна нулю:
Силы, для которых выполняется данное условие, называются консервативными или потенциальными. Работа консервативных сил на любом замкнутом пути равна нулю. Поэтому потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути равна нулю. Поскольку работа в потенциальном поле сил на замкнутом пути равна нулю, то на одних участках замкнутого пути силы совершают положительную работу, а на других – отрицательную. Все силы, не удовлетворяющие этому условию, называются неконсервативными.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 7739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.65.134 (0.011 с.) |

 или
или  , (6.1)
, (6.1) , (6.2)
, (6.2) . (6.3)
. (6.3)
 в случае плоской волны, распространяющейся в направлении оси X (рис. 6.1). Пусть плоская стенка совершает гармоническое колебание, согласно выражению
в случае плоской волны, распространяющейся в направлении оси X (рис. 6.1). Пусть плоская стенка совершает гармоническое колебание, согласно выражению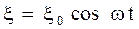 . (6.5)
. (6.5) .
. . (6.6)
. (6.6) . (6.7)
. (6.7) ;
; ; (6.10)
; (6.10) , (6.11)
, (6.11) . (6.12)
. (6.12) . (6.13)
. (6.13) .
. ;
;  . (6.14)
. (6.14) ;
;  . (6.15)
. (6.15)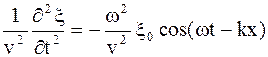 или
или  . (6.16)
. (6.16) . (6.17)
. (6.17)
 . (6.17)
. (6.17)

 . (6.19)
. (6.19) ; (6.20)
; (6.20) . (6.21)
. (6.21) . (6.22)
. (6.22) ,
, . (6.23)
. (6.23) . (6.24)
. (6.24) . (6.25)
. (6.25) Рис.6.2
Рис.6.2
 Рис.6.3
Рис.6.3
 . (6.26)
. (6.26) . (7.2)
. (7.2) образует с направлением движения постоянный угол
образует с направлением движения постоянный угол  . Поэтому выражению (7.2) в данном случае можно придать следующий вид:
. Поэтому выражению (7.2) в данном случае можно придать следующий вид: . (7.3)
. (7.3) , взяв их столь малыми, что за время прохождения телом такого участка можно было бы считать силу постоянной. Тогда на каждом элементарном участке пути DS1работа силы равна
, взяв их столь малыми, что за время прохождения телом такого участка можно было бы считать силу постоянной. Тогда на каждом элементарном участке пути DS1работа силы равна . (7.4)
. (7.4) . (7.5)
. (7.5) . (7.6)
. (7.6) Рис.7.1
Рис.7.1
 численно равна площади заштрихованной полоски, а работа
численно равна площади заштрихованной полоски, а работа  на пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой Ft(S), вертикальными прямыми 1 и 2 и осью OS.
на пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой Ft(S), вертикальными прямыми 1 и 2 и осью OS. , (7.7)
, (7.7) – удлинение пружины.
– удлинение пружины. . (7.8)
. (7.8) . (7.9)
. (7.9) . (7.10)
. (7.10)
 . (7.11)
. (7.11)


