
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каждая точка фронта волны является источником вторичных волн.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Каждая точка фронта волны является источником вторичных волн. Закон прямолинейного распространения света. В однородной среде свет распространяется по прямым линиям Закон независимости световых пучков. Световой поток можно разбить на отдельные световые пучки, выделяя их, например, при помощи диафрагм. Действие этих пучков оказывается независимым, т.е. суммарный эффект представляет собой сумму вкладов каждого светового пучка в отдельности. Ограниченность этого закона проявляется в явлениях интерференции света. Закон отражения Используя принцип Гюйгенса можно доказать закон отражения электромагнитных волн на границе раздела двух диэлектриков. Угол падения равен углу отражения. Лучи, падающий и отраженный, вместе с перпендикуляром к границе раздела двух диэлектриков, лежат в одной плоскости. Ð a = Ð b.
Закон преломления Оптически однородная среда 1 характеризуется абсолютным показателем преломления где с - скорость света в вакууме; v1 - cкорость света в первой среде. Аналогично для n2. Отношение n2 / n1 = n21 называют относительным показателем преломления второй среды относительно первой Если скорость распространения света в первой среде v1, а во второй - v2,
то за Dt прохождения падающей плоской волной расстояния АО1 в первой среде АО1 = v1Dt. Фронт вторичной волны достигает точек полусферы, радиус которой ОВ = v2Dt. Новый фронт волны, распространяемой во второй среде, изображается плоскостью ВО1, а направление ее распространения - лучами ОВ и О1С (перпендикулярными к фронту волны). Угол b между лучом ОВ и нормалью к границе раздела двух диэлектриков в точке О называют углом преломления. Из треугольников ОАО1 и ОВО1 следует, что АО1 = ОО1 sin a, OB = OO1 sin b. => Закон преломления:
Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления двух сред.
Полное внутреннее отражение Согласно закону преломления на границе раздела двух сред можно наблюдать полное внутреннее отражение, если n1 > n2, т. е. Ðb >Ða. Следовательно, существует такой предельный угол падения Ðaпр, когда Ðb = 900. Тогда закон преломления принимает следующий вид: sin aпр = При дальнейшем увеличении угла падения Ða > Ðaпр свет полностью отражается от границы раздела двух сред.
Отражение — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными оптическими свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения). Преломление (рефракция) — изменение направления распространения волн электромагнитного излучения, возникающее на границе раздела двух прозрачных для этих волн сред или в толще среды с непрерывно изменяющимися свойствами. Поглощение света - уменьшение интенсивности оптического излучения (света), проходящего через материальную среду, за счёт процессов его взаимодействия со средой. Световая энергия при поглощении света переходит в различные формы внутренней энергии среды; она может быть полностью или частично переизлучена средой на частотах, отличных от частоты поглощённого излучения. Рассеяние света — рассеяние электромагнитных волн видимого диапазона при их взаимодействии с веществом. При этом происходит изменение пространственного распределения, частоты, поляризации оптического излучения, хотя часто под рассеянием понимается только преобразование углового распределения светового потока. Закон сохранения энергии в оптике: Из этого равенства непосредственно следует одно из соотношений Мэнли — Роу: ω1 + ω2 = ω3,которое, собственно, и выражает тот факт, что частота генерируемого излучения равна сумме частот двух исходных волн. 3. Волновая оптика — раздел оптики, который описывает распространение света с учётом его волновой природы. Явления волновой оптики — интерференция, дифракция, поляризация и т. п. Электромагнитная природа света Свет представляет собой видимый участок спектра электромагнитных волн, длины волн которых занимают интервал от 0.4мкм до 0.76мкм. Каждой спектральной составляющей оптического излучения может быть поставлен в соответствие определённый цвет. Окраска спектральных составляющих оптического излучения определяется их длиной волны. Цвет излучения изменяется по мере уменьшения его длины волны следующим образом: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Предположим, что напряжённость электрического поля и магнитная индукция являются произвольными функциями следующей комбинации координат и времени: где
и они перпендикулярны вектору Спектр видимого излучения При разложении луча белого цвета в призме образуется спектр, в котором излучения разных длин волн преломляются под разным углом. Цвета, входящие в спектр, то есть такие цвета, которые могут быть получены световыми волнами одной длины (или очень узким диапазоном), называются спектральными цветами. Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой λ. По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина
Получить соотношение, связывающее длину волны с фазовой скоростью (v) и частотой(f) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний T, поэтому
где λ0 - длина волны в вакууме. Уравнение плоской электромагнитной волны.
этой же частотой Уравнения сферической монохроматической электромагнитной волны можно записать в следующем виде:
В комплексной форме эти уравнения принимают вид: Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу. Волновой вектор обычно обозначается латинской буквой Волновое число связано с длиной волны λ соотношением: Связь между волновым вектором и частотой задаётся законом дисперсии. Все возможные значения волновых векторов образуют обратное пространство или k-пространство. Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Если источником волны является точка, то волновые поверхности в однородном и изотропном пространстве представляют собой концентрические сферы. Типы волновых поверхностей (на примере света): · Для аморфных сред эта поверхность имеет форму сферы. Свет распространяется одинаково во всех направлениях. · Для кубических кристаллов эта поверхность также имеет форму сферы. · В кристаллах средних сингоний происходит двулучепреломление. Свет, вошедший в кристалл, распадается на обыкновенный и необыкновенный лучи. Поэтому поверхность показателей преломления состоит из эллипсоида вращения и сферы. В том случае, если сфера вписана в эллипсоид, кристалл называется оптически отрицательным, если же эллипсоид вписан в сферу, кристалл называется оптически положительным. · В кристаллах нижних категорий тоже происходит двулучепреломление. Свет, вошедший в кристалл, распадается на два необыкновенных луча. Волновая поверхность имеет сложную форму. Оптический знак определяется по виду индикатрисы. Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Интенсивность волны - средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны. Интенсивность волны пропорциональна квадрату её амплитуды. Для характеристики интенсивности волнового процесса используют три параметра: амплитуда волнового процесса, плотность энергии волнового процесса и плотность потока энергии. Вопрос. Явление наложения когерентных световых волн, в результате которого наблюдается чередование усиления света в одних точках пространства и ослабления в других, называют интерференцией света. Когерентность - согласованное протекание во времени и в пространстве нескольких колебательных или волновых процессов, позволяющих получать при их сложении четкую интерференционную картину. Монохроматичность − это свойство осциллятора излучать свет строго определённой частоты и амплитуды в течение бесконечно долгого времени. Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны – не ограниченные в пространстве волны одной определенной и строго постоянной частоты. Когерентность колебаний, совершаемых в одной и той же точке пространства, но в разные моменты времени, называют временнойкогерентностью. Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию от монохроматического света, называют пространственно когерентными Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга tког называется временем когерентности. Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние lког =сtког, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность.
Оптическая разность хода - это разность оптических длин путей световых волн, имеющих общие начальную и конечную точки. (r2 - r1)×n = d - оптическая разность хода складываемых волн Разность фаз складываемых волн Dj = j2 - j1 = и не зависит от времени, где j2 = w t - kr 2 + j02; j1 = w t - kr 1 + j01. Согласно принципу суперпозиции вектор напряженности результирующего колебания равен геометрической сумме векторов напряженности складываемых волн, т. е.
Закон независимости световых пучков:
· эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.
Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо.
Вопрос. Методы получения когерентных волн и интер картины
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S1 и S2, параллельные щели S.
Таким образом, щели S1 и S2 играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.
2.Бипризма Френеля.
Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S1 и S2, являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.
3.3. Оптическая длина пути и разность хода
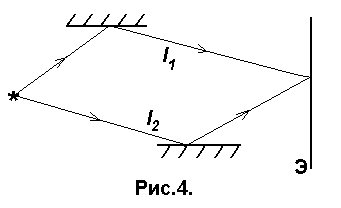
Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l1 и l2 в средах с абсолютными показателями преломления n1 и n2 соответственно (рис.4).
Условия максимумов и минимумов интерференционной картины
В результате наложения двух или более когерентных волн в пространстве возникает интерференционная картина, представляющая собой чередование максимумов и минимумов интенсивности света, а значит, и освещенности экрана.
Интенсивность света в данной точке пространства определяется разностью фаз колебаний φ1 – φ2. Если колебания источников синфазны, то φ01 – φ02 = 0 и
Разность фаз определяется разностью расстояний от источников до точки наблюдения Δr = r1 – r2 (разность расстояний называется разностью хода). В тех точках пространства, для которых выполняется условие
волны, складываясь, усиливают друг друга, и результирующая интенсивность в 4 раза превосходит интенсивность каждой из волн, т.е. наблюдается максимум. Напротив, при
волны гасят друг друга (I = 0), т.е. наблюдается минимум. Опыт Юнга. Опыт Юнга - опыт по интерференции света от двух точечных источников, полученных пропусканием пучка света от общего источника через два отверстия. Опыт Юнга позволяет оценить длину волны для различных участков спектра.
6ой ВОПРОС. · Интерференция света в тонких пленках (плоскопараллельных и клиновидных). Полосы равного наклона и равной толщины. 1.
На рисунке изображена Интерференция в плоскопараллельной пластинке 2.
На рисунке изображена интерференция на клиновидной пластинке. 1. Полосы равного наклона.
2. Полосы равной толщины.
Интерференционные полосы на поверхности пленки имеют одинаковую освещенность на всех точках поверхности, соответствующих одинаковым толщинам пленки, и называются полосами равной толщины. Ой ВОПРОС. · Кольца Ньютона. Интерференция при большой разности хода, отражение от толстой плоскопараллельной пластинки. Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. интерференцию при большой разности хода можно наблюдать только с помощью источника монохроматического света, или, по крайней мере, с помощью источника света, имеющего линейчатый спектр с редкими и тонкими спектральными линиями. отражение от толстой плоскопараллельной пластинки: Все лучи, падающие на пленку под одним и тем же углом, разделяются на 2 луча и после отражений от поверхностей пленки имеют одно и то же направления распределения, будучи параллельными друг другу. Формулы Эйри. · Формула для прошедшей волны Предположим, что на пластинку падает под углом
Мы считаем здесь размеры пластинки и линзы достаточно большими, чтобы можно было не учитывать дифракцию на их краях и виньетирование наклонных пучков (т.е ограничение их поперечного сечения краями пластинки и линзы). Для нахождения интенсивности прошедшей волны умножим E 2 в формуле на комплексно-сопряженную величину и воспользуемся формулами для энергетического коэффициента отражения:
Таким же способом легко получить выражения для амплитуды и интенсивности отраженной волны.
· Формула для отраженной волны Тем же способом, каким мы получили выражение для амплитуды прошедшей волны, легко получить выражение для амплитуды отраженной волны:
Здесь учтено, что
· Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. · Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. · Метод зон Френеля (строим волновую поверхность, на ней отмечаем границы зон - они удалены от точки экрана на полуцелое число длин волн. Если таких зон четное число, в точке экрана освещенность 0, если нечетное - освещенность положительная). · Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом зонная пластинка действует как собирающая линза.
· Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия.
Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами,
где, знак плюс соответствует нечетным m, минус - четным m.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А1, т.е.вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное - то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины. Расчет амплитуды результирующего колебания на вне осевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены. Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Am ≪ A1и результирующая амплитуда A = A1/2,т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно. · Теорема Бабине (в теории дифракции) – теорема, согласно которой Фраунгоферовы дифракционной картины от каждого из дополнительных экранов, получаемые в фокальной плоскости линзы, одинаковы для любой точки, за исключением самого фокуса.
Источник: http://page-book.ru/i320312 Детлаф А.А. Яворский Б.М. Курс физики. Том III Волновые процессы. Оптика. Атомная и ядерная физика (стр. 188-191)
Основные характеристики Заряженная частица - электрон. Порог v > c/n, Вещество прозрачно для черенковского излучения, т.е. |Im ε| ~<< Re Пороговая энергия (в МэВ)
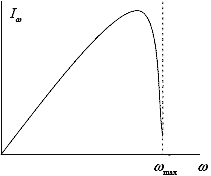
Спектр Спектр непрерывный, практически нарастающий линейно до ωmax при n(ωmax) = c/v;
Интегральная энергия излучения (в эВ/см)
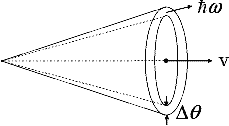
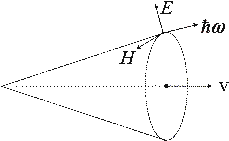
Угловые характеристики Конус с угловым раствором
Интервал углов Поляризация излучения Вектор электрического поля фотона лежит в плоскости скорости v и напавления излучения.
Поляризация света (=Поляризация волн) Поляризация волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения. Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.021 с.) |


 ,
, Рис. 3
Рис. 3
 .
. , (sin 900=1)
, (sin 900=1)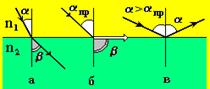 Рис. 4
Рис. 4


 — некоторый постоянный вектор. В этом случае
— некоторый постоянный вектор. В этом случае  и
и  удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь:
удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь:

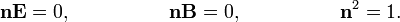
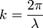 , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.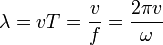
 Вследствие дисперсии при переходе света из одной среды в другую длина волны изменяется прямо пропорционально скорости его распространения. Поскольку длина волны излучения прямо пропорциональна скорости его распространения, получаем для абсолютного показателя преломления еще одну формулу:
Вследствие дисперсии при переходе света из одной среды в другую длина волны изменяется прямо пропорционально скорости его распространения. Поскольку длина волны излучения прямо пропорциональна скорости его распространения, получаем для абсолютного показателя преломления еще одну формулу: При прохождении монохроматической электромагнитной волны частотой ω векторы E и H в данной фиксированной точке пространства испытывают синфазные, и только синфазные гармонические колебания с
При прохождении монохроматической электромагнитной волны частотой ω векторы E и H в данной фиксированной точке пространства испытывают синфазные, и только синфазные гармонические колебания с



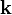 и измеряется в обратных сантиметрах.
и измеряется в обратных сантиметрах.
 (СГС)
(СГС)  (СИ), где E и H — вектора напряжённости электрического и магнитного полей соответственно.
(СИ), где E и H — вектора напряжённости электрического и магнитного полей соответственно.
 =сonst
=сonst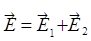 .
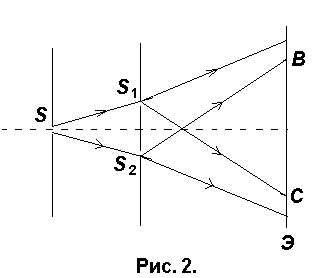
.

 . (1)
. (1) . (2)
. (2) . (3)
. (3)

 плоская монохроматическая волна с амплитудой E 0. При нахождении комплексной амплитуды суммарной волны, прошедшей через пластинку, нужно учесть, что фаза каждой последующей волны больше фазы предыдущей на
плоская монохроматическая волна с амплитудой E 0. При нахождении комплексной амплитуды суммарной волны, прошедшей через пластинку, нужно учесть, что фаза каждой последующей волны больше фазы предыдущей на 
 - волновое число. Поэтому комплексная амплитуда последующей волны отличается дополнительным множителем
- волновое число. Поэтому комплексная амплитуда последующей волны отличается дополнительным множителем  от амплитуды предыдущей. В результате комплексная амплитуда всей прошедшей волны представится геометрической прогрессией:
от амплитуды предыдущей. В результате комплексная амплитуда всей прошедшей волны представится геометрической прогрессией:


 . Для интенсивности отраженной волны находим
. Для интенсивности отраженной волны находим



 где
где  – минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с близкими значениями
– минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с близкими значениями  и
и  считаются разрешенными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии. Рис. поясняет критерий Рэлея.
Так как спектральные линии, изображенные на рис. некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея.
считаются разрешенными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии. Рис. поясняет критерий Рэлея.
Так как спектральные линии, изображенные на рис. некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея.
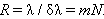 Порядок спектра
Решетка способна разлагать свет в спектр. Для этого могут быть использованы дифракционные максимумы различных порядков (кроме m = 0). Практически, однако, используются главные максимумы, расположенные в пределах основного лепестка диаграммы излучения одиночной щели, имеющего полуширину
Порядок спектра
Решетка способна разлагать свет в спектр. Для этого могут быть использованы дифракционные максимумы различных порядков (кроме m = 0). Практически, однако, используются главные максимумы, расположенные в пределах основного лепестка диаграммы излучения одиночной щели, имеющего полуширину  . Т.е макс порядок спектра
. Т.е макс порядок спектра  Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3.
Правило Релея
Условие Δl = r называют критерием разрешения Релея
расстояние Δl между центрами дифракционных изображений
r центрального светлого пятна
Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3.
Правило Релея
Условие Δl = r называют критерием разрешения Релея
расстояние Δl между центрами дифракционных изображений
r центрального светлого пятна
 Угловая дисперсия
По определению, угловой дисперсией D называется величина:
Угловая дисперсия
По определению, угловой дисперсией D называется величина:
 δ - знак дифференциала. d - обозначает постоянную решетки.
В определении угловой дисперсии δλ - разность длин волн двух соседних линий, δφ - соответствующая разность углов, под которыми наблюдаются главные максимумы.
Линейная дисперсия
δ - знак дифференциала. d - обозначает постоянную решетки.
В определении угловой дисперсии δλ - разность длин волн двух соседних линий, δφ - соответствующая разность углов, под которыми наблюдаются главные максимумы.
Линейная дисперсия
 где l - расстояние вдоль экрана наблюдения, δl - расстояние между линиями на экране.
15 Вопрос
Дифракция на пространственной решетке
Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат.
Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной.
Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:
где l - расстояние вдоль экрана наблюдения, δl - расстояние между линиями на экране.
15 Вопрос
Дифракция на пространственной решетке
Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат.
Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной.
Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:  и
и  где φ - угол между направлением на главный максимум (направление луча) и нормалью к решетке; m – порядок дифракционного максимума.
Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос.
Условия максимума для трехмерной решетки
Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:
где φ - угол между направлением на главный максимум (направление луча) и нормалью к решетке; m – порядок дифракционного максимума.
Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос.
Условия максимума для трехмерной решетки
Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:  , (m = 1, 2, 3,....). Из формулы видно, что дифракция будет наблюдаться лишь при. Т. е. при условии будут отсутствовать дифракционные максимумы. Поэтому условие называют условием оптической однородности кристалла. Из формулы следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу.
16)
Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества.
формула вульфа-брега.
2dsin(a) = nl
l - длинна волны.
a – угол «скольжения», угол между направлением пучка, и «поверхностью кристаллической решетки»
n – 1,2,3,....
Рентгенография — исследование внутренней структуры объектов, которые проецируются при помощи рентгеновских лучей на специальную плёнку или бумагу.
17)
Голография — набор технологий для точной записи, воспроизведения и переформирования волновых полей.
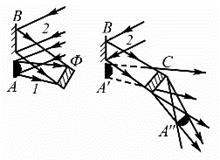
схема получения объемных голографических изображений. Суть этого метода состоит в следующем: c помощью фотопластинки Ф (рис. 3.8) регистрируется интерференционная картина, возникающая при наложении волны 1, рассеянной объектом А (так называемой предметной волны), и когерентной ей волны 2, имеющей фиксированные значения амплитуды и фазы. Волна 2 называется опорной волной (опорным пучком). Она испускается тем же источником света, который освещает объект А, и после отражения от зеркала В падает непосредственно на фотопластинку Ф. Интерференционную картину, зафиксированную на фотопластинке после ее проявления, называют голограммой объекта.
Для восстановления изображения голограмма С помещается в то же самое положение, где она находилась до регистрации. Ее просвечивают, как диапозитив, той же опорной волной 2, которая использовалась для получения голограммы. Однако вторая часть опорного пучка перекрывается диафрагмой. Падающая световая волна дифрагирует на голограмме. В результате дифракции наблюдаются два объемных изображения объекта: мнимое и действительное. Мнимое изображение A' находится в том же месте по отношению к голограмме, где помещается объект А при съемке голограммы. Действительное изображение A'' располагается по другую сторону голограммы. Оно имеет рельеф, обратный рельефу предмета, что создает определенные неудобства. Обычно пользуются мнимым голографическим изображением, которое по зрительному восприятию тождественно самому предмету.
, (m = 1, 2, 3,....). Из формулы видно, что дифракция будет наблюдаться лишь при. Т. е. при условии будут отсутствовать дифракционные максимумы. Поэтому условие называют условием оптической однородности кристалла. Из формулы следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу.
16)
Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества.
формула вульфа-брега.
2dsin(a) = nl
l - длинна волны.
a – угол «скольжения», угол между направлением пучка, и «поверхностью кристаллической решетки»
n – 1,2,3,....
Рентгенография — исследование внутренней структуры объектов, которые проецируются при помощи рентгеновских лучей на специальную плёнку или бумагу.
17)
Голография — набор технологий для точной записи, воспроизведения и переформирования волновых полей.
схема получения объемных голографических изображений. Суть этого метода состоит в следующем: c помощью фотопластинки Ф (рис. 3.8) регистрируется интерференционная картина, возникающая при наложении волны 1, рассеянной объектом А (так называемой предметной волны), и когерентной ей волны 2, имеющей фиксированные значения амплитуды и фазы. Волна 2 называется опорной волной (опорным пучком). Она испускается тем же источником света, который освещает объект А, и после отражения от зеркала В падает непосредственно на фотопластинку Ф. Интерференционную картину, зафиксированную на фотопластинке после ее проявления, называют голограммой объекта.
Для восстановления изображения голограмма С помещается в то же самое положение, где она находилась до регистрации. Ее просвечивают, как диапозитив, той же опорной волной 2, которая использовалась для получения голограммы. Однако вторая часть опорного пучка перекрывается диафрагмой. Падающая световая волна дифрагирует на голограмме. В результате дифракции наблюдаются два объемных изображения объекта: мнимое и действительное. Мнимое изображение A' находится в том же месте по отношению к голограмме, где помещается объект А при съемке голограммы. Действительное изображение A'' располагается по другую сторону голограммы. Оно имеет рельеф, обратный рельефу предмета, что создает определенные неудобства. Обычно пользуются мнимым голографическим изображением, которое по зрительному восприятию тождественно самому предмету.




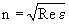 .
. .
.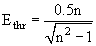 ,
, n = n(ω). Так для воды при длине волны излучения ~0.4 мкм n ~1.3 и Ethr ~0.5 МэВ.
n = n(ω). Так для воды при длине волны излучения ~0.4 мкм n ~1.3 и Ethr ~0.5 МэВ. ωmax ~ < 10 - 30 эВ (ближний ультрафиолет; при больших частотах излучение происходит лишь в отдельных узких интервалах энергий). Спектральная интенсивность (на единицу пути)
ωmax ~ < 10 - 30 эВ (ближний ультрафиолет; при больших частотах излучение происходит лишь в отдельных узких интервалах энергий). Спектральная интенсивность (на единицу пути)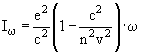 .
.
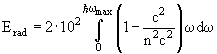 .
.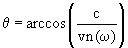 .
.
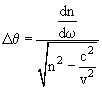 .
.


