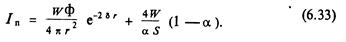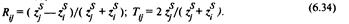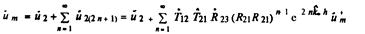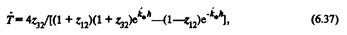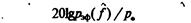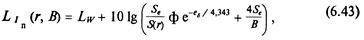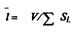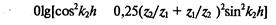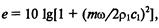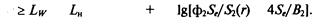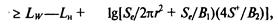Уравнение плоской волны, не затухающей с расстоянием, в комплексной форме имеет вид

U=u_me^j(wt-kr)

здесь u_m = u_m^jфu – комплексная амплитуда; r – радиус-вектор рассматриваемой точки; k –волновой вектор, численно равный волновому числу

k=w/c=2π/λ

где с λ – соответственно скорость распространения и длина волны.

Распространение волны всегда связано с переносом энергии, которая количественно характеризуется мгновенным вектором плотности потока энергииIt. На практике обычно пользуются понятием интенсивности волны I, которая равна модулю среднего значения вектораItза время, равное периоду T полного колебания. Найдем интенсивности звука и электромагнитной волны. Для этого введем понятие импеданса среды при распространении волны.

Комплексным импедансом среды при распространении звуковой волны назовем отношение

где р и v – соответственно звуковое давление и колебательная скорость.

Комплексным импедансом среды при распространении электромагнитной волны назовем отношение поперечных составляющих электрического (Е) и магнитного (Н) полей в данной точке:

z=E/H

Положив u=p для звука и u=E для электромагнитного поля, можно для определения интенсивности звуковой волны или для определения интенсивности электромагнитной волны использовать одну и ту же формулу*:

i-^^-^-^^ ^w

Эффективное значение величины u

где

При заданных стандартом референтных значениях. I*U*Z* удовлетворяющих условию I* = U*/Z* из соотношения (6.25) следует

L_I=L_U+L_Z

**Числовые значения референтных величин различны для звука и ЭМП.

L_I=101gI/I*, *(6.26)–

где L_U=201gu_эф/Г*Г; L_Z=101gz/z* уровни величин I,U,Z. Суммарная интенсивность некогерентных источников

Следовательно, уровень суммарной интенсивности

где Lit, и п – соответственно уровень интенсивности i-го источника и число источников. Если все п источников имеют одинаковый уровень интенсивности, равный Lt, то уровень суммарной интенсивности будет равен

L_IE=L_I+101gn

Источники направленного действия характеризуют коэффициентом направленности, равным отношению:

Ф=I/I_H

где I– интенсивность волны в данном направлении на некотором расстоянии r от источника направленного действия мощностью W, излучающего волновое поле в телесный угол Ω; Iн= W/(4πr²) – интенсивность волны на том ж е расстоянии при замене данного источника на источник ненаправленного действия той же мощности. В общем случае в сферической системе координат, характеризуемой углами ø и φ, коэффициент направленности φ= φ(ø). Для осесимметричных источников коэффициент направленности не зависит от координаты ф и ф=ф(ø). Таким образом, интенсивность можно выразить через мощность источника следующим образом:

При необходимости учесть затухание в уравнение (6.23) вводят вместо волнового числа k комплексное волновое число fc, или коэффициент распространения k:

где γ и δ – соответственно коэффициент фазы и коэффициент затухания. Амплитуда затухающей волны будет равна um (δ) = u_meδr a интенсивность волны будет затухать по закону:

На расстоянии r затухание в децибеллах

где δо = 8,686δ – коэффициент затухания, выраженный в децибелах на единицу длины.

Полагая Wx =I*Seиз выражения (6.28) находим уровень интенсивности с учетом затухания:

где Se и Lw=101gW/W* – соответственно единичная площадь и уровень мощности относительно референтного значения W*:

Таким образом, уровень интенсивности в данной точке определяется через уровень мощности и коэффициент направленности. Формула (6.29) справедлива в свободном волновом поле, т. е. поле, не имеющем границ, от которых могло бы происходить отражение волн. Свободное поле можно создать и в помещении, если сделать последнее из материала, полностью поглощающего энергию падающей волны. Величину 101gф называют показателем направленности и обозначают ПН.

Таблица 6.7. Коэффициент затухания звука в воздухе, дБ/км

Относительная влажность возду-	Среднегеометрические частоты октавных полос, Гц
ха,%
	0.8	1,5	3,8	12,1
	0,4	1,3	2,8	4,9
	0,2	0,9	2,7	5,5	9,7

 

Для звука коэффициент затухания δо зависит от частоты звука, температуры, давления и относительной влажности воздуха. При нормальном атмосферном давлении и температуре воздуха, равной +20 °С, значения коэффициента δо даны в табл. 6.7. Для электромагнитной волны, распространяющейся в воздухе, δо≈0 (см. ниже). Следует иметь в виду, что в реальных условиях уровень затухания зависит также от погодных условий (дождь, снег, туман и т. д.), наличия растительности (трава, кустарник, деревья и т. д.), состояния атмосферы (ветер, туман, турбулентность, температурные градиенты и т. д.), наличия отражающих поверхностей (земля, преграды, экраны и т. д.) и ряда других факторов и вычисляется по формуле где eS(i) – уровень

 

затухания при наличии i-го фактора. Если затуханием можно пренебречь (S = 0), то уровень интенсивности:

Диффузное волновое поле в изолированных объемах. Волновое поле называют диффузным, если усредненная по времени объемная плотность энергии W=Wg одинакова во всех точках, а поток энергии через единичную площадку в любой точке и в любом направлении постоянен и равен 1g

Энергия волны в объеме d V равна ck=WgdK В диффузном поле эта энергия распределяется равномерно во все стороны пространства 4я. Следовстгельно, на телесный угол dQ = d5fcos6/r² приходится часть энергии, равная d^ == w^cosOd V(\S/^nr¹. В сферической системе координат с полярным углом 9 элементарный объем d^=" AinOdOdcpdr и полная энергия через площадку d*? найдется в результате следующего интегрирования:

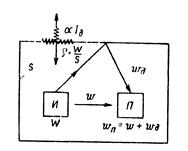
Откуда следует, что поток энергии через единичную площадку

Ig=Wgc/4=Iв/4

Таким образом, поток энергии через единичную площадку в диффузном волновом поле в четыре раза меньше интенсивности Iв бегущих волн с той же объемной плотностью энергии. Для бегущей со скоростью с волны интенсивность I = cw, где w – усредненная объемная плотность энергии. При наличии диффузного поля понятие интенсивности теряет смысл.

Понятие диффузного поля часто используют при определении плотности потока энергии Iп в изолированных объемах. Под изолированным объемом понимается пространство, огражденное стенками (например, производственное помещение, кабина, пространство под кожухом машины и т. д.). Волны в изолированных объемах, многократно отражаясь, образуют поле, которое изменяется при изменении геометрических размеров, формы и других характеристик источника.

Волновое поле в каждой точке изолированного объема можно представить в виде совокупности волн, непосредственно приходящих в эту точку от источника, именуемую как прямая волна, и совокупности волн, попадающих в нее после отражений от границ изолированного объема – отраженная волна.

Плотность энергии Wп в любой точке изолированного объема будет складываться (рис. 6.38) из плотности энергии w прямой волны и плотности энергии Wg при диффузном поле отраженной волны: Wп = w + Wg. Умножив это уравнение на скорость с, получим

Iп=I+4Ig

Интенсивность прямой волны в общем случае определяется формулой (6.28). Выразим плотность потока энергии Ig через мощность источника. При работе источника в изолированный объем постоянно поступает энергия. При мощности источника W отраженный от границ полный поток энергии составит pW, а от единичной площадки pW/S. За единицу времени через единичную площадку границы вследствие поглощения исчезнет количество энергии, равное αIg. Так как в диффузном поле плотность энергии постоянная, то должно соблюдаться равенство рW/S=αIg. Для простоты дальнейших рассуждений здесь предполагается, что коэффициент а значительно больше коэффициента т. Уравнение (6.32) принимает вид

Рис. 6.38. Диффузное поле отраженной волны

 

Из полученного выражения видно, что в изолированном объеме плотность потока энергии получает некоторое приращение, которое аналитически обусловлено наличием множителя (1–α)/α, который велик при коэффициенте α близком к нулю.

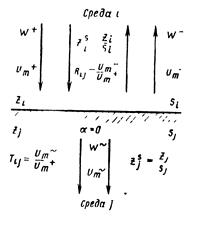
Защитное устройство бесконечной толщины. Во многих случаях информацию можно получить, исследуя вместо реальной конструкции теоретическое защитное устройство бесконечной толщины, оно представляет собой просто среду, бесконечно простирающуюся в направлении распространения волны. Таким образом, волна из одной среды проходит в другую среду (защитное устройство), предварительно попадая на границу раздела этих сред. При падении на плоскую границу раздела двух разных сред плоская волна частично отражается, частично проходит в другую среду, оставаясь плоской, но меняя при этом свое направление распространения, т. е. преломляясь. Таким образом в общем случае существуют три волны: падающая, отраженная и преломленная (прошедшая).

При прохождении границы раздела сред без поглощения должен соблюдаться закон сохранения энергии: W^- + W˜ = W⁺. Кроме того, на границе должны выполняться специфические для волн данной природы условия: например, для звуковых волн по обе стороны границы должны быть равны звуковые давления – принцип непрерывности звукового давления; для электромагнитных волн на границе раздела двух сред непрерывны тангенциальные составляющие электромагнитного поля. Условие непрерывности при нормальном падении волн можно записать в виде равенства на границе амплитуд поля в среде j и среде j:[um]j=[um]. Усредненный поток энергии можно выразить через интенсивность: W= IS, а интенсивность – через амплитуду и импеданс среды с помощью формулы (6.25). Тогда закону сохранения энергии можно придать виц (рис. 6.39)

W и т, U т, и т – амплитуда, соответственно, падающей, отраженной и прошедшей волн, a z k = Zk/Sk – импеданс на единицу площади (k = /, у).

В среде i существуют падающая и отраженная волна, которые на границе создают суммарную амплитуду [u,n]i == и^т ⁺ "w» в среде у существует только преломленная волна:

[Urn]} ⁼⁼ иЩ. Условие непрерывности и закон сохранения энергии позволяют найти амплитудный коэффициент отражения Ry и амплитудный коэффициент передачи Тц при' падении волны на границу (/, j) из среды /:

При этом имеем Ту = 1 + 7?у, Ry = – Rj,. Так как значение коэффициента отражения лежит между –I и +1, то значение коэффициента передачи заключено в интервале от 0 до 2 и он всегда положителен. При равных площадях (S, = Sj) соотношения (6.34) примут такой же вид, который можно получить простой заменой ^ на ^, а при равных импсдансах сред to == ^) – заменой ^ на \/S„ (k = /, /). Амплитудные коэффициенты отражения и передачи при нормальном падении волн связаны с соответствующими энергетическими коэффициентами соотношениями:

Защитное устройство конечной толщины. В общем случае защитное устройство имеет конечную толщину. При этом волна, падая на защитное устройство, частично отражается, а частично может проходить сквозь него. Отражательную способность защитного устройства характеризуют коэффициентом отражения энергетическим и амплитудным. Прозрачные свойства защитою устройства характеризуют соответствующими коэффициентами передачи. Амплитудные коэффициенты отражения и передачи па границах разных сред будем обозначать соответственно через Ry и t{j. Эти величины определены соотношениями (6.34). Амплитудные коэффициенты отражения и передачи защитного устройства будем обозначать соответственно через R и Г, при этом в комплексной форме

где U⁺ _т и U _т^- – соответственно амплитуда падающей и отраженной волны на входе в защитное устройство; U_т – амплитуда волны на выходе из защитною устройства.

Рассмотрим случай, когда гармоническая волна падает из среды 1 (рис. 6.40) на защитное устройство произвольной толщины h, состоящее из среды 2, ограниченной с другой стороны средой з, при этом S₁ = S₂ = S₃. Примем, что импедансы сред соответственно равны Z₁, Z₂, Z₃ волновое поле в среде 2 на длине h затухает по экспоненциальному закону е, где h – коэффициент распространения. При неравных импедансах сред часть энергии на границе (7, 2) отражается обратно в среду 7 в соответствии с формулой (6.34). Амплитуда падающей волны равна и+^п- Обозначив амплитуду отраженной волны через U, имеем: U= R_um.

Другая часть энергии пройдет в среду 2 и, изменившись пропорционально коэффициенту передачи Гц на границе (7, 2), претерпит в среде 2 затухание по закону е², так что амплитуда волны в среде 2, которую обозначим через U, определится выражением й\ = Т^е^й+т- Эта волна на границе (2, 3) частично отразится и создаст в среде 2 отраженную волну, амплитуда которой с учетом затухания станет равной й^ == ^R^T^e'²^ и частично пройдет в среду J. Амплитуда прошедшей волны будет равна ид = ^^ТчзТ^ ^hu-^m. Волна с амплитудой йч, частично пройдет в среду 7: и^ =Г2l7l27г23^^-2u^⁴m, а частично отразится от границы (7, 2^ и снова будет распространяться в среде 2 в виде волны с амплитудой us = rzi ТЬ^зе"³^-* /и. Процесс отражения и прохождения волн на границе сред (1, 2 и 2, 3) будет продолжаться до полного затухания волн

 

Рис. 6.39. Баланс энергии на границе раздела сред

Рис. 6.40. Схема защитного устройства конечной толщины

 

Суммируя все волны, из которых в среде 7 формируется общая отраженная волна, можно получить для амплитуды этой волны следующее выражение

Пользуясь формулой бесконечной геометрической прогрессии, найдем амплитудный коэффициент отражения защитного устройства

В среде 3 суперпозиция распространяющихся волн создаст волну, прошедшую сквозь защитное устройство. Амплитуда этой волны на выходе из защитного устройства

Просуммировав, получим согласно формуле (6.35) амплитудный коэффициент прозрачности защитного устройства конечной толщины:

С помощью формул (6.34) преобразуем коэффициенты R и Г к виду:

где zi2 ⁼ а/О и 02 = o/q. Полученные соотношения носят общий характери их можно применять при решении задач защиты как от звуковых, так и от электромагнитных полей,

Если по обе стороны от защитного устройства находится одна и та же среда, то импедансы ^и ^ равны. Тоща формулы (6.36) и (6.37) преобразуются к виду:

Амплитудные коэффициенты R и Т при нормальном падении волн связаны с энергетическими коэффициентами р и т соотношениями: р = В. ², т = Г², эффективность защиты

В некоторых случаях для расчета эффективности защиты удобно использовать следующую запись:

е = е. + е + <?., (6.40)

Ж f. Л ^

где ^ = (201g^)8A, ^ = 201g|T U вц = 201g|(l– рце^-2V)! – слагаемые эффективности за счет ослабления волн соответственно в материале защитного устройства, при прохождении границы раздела сред (1, 2) и при многократных отражениях внутри защитного устройства. Так как с увеличением частоты коэффициент h возрастает, то ^ -> 0 и эффективность изоляции высокочастотных полей е w ek •+- е^

Прогнозирование шума. Условие безопасности при наличии звукового поля можно записать в виде неравенства

L,(f) ^(Д (6.41)

где Lp(f) = 201gp^(/)/A и 1н(/) –соответственно уровни звукового давления и их нормативные значения. Неравенство (6.41) должно выполняться на всех среднегеометрических частогах/== 63,125, 250, 500,1000, 2000, 4000, 80000 Гц и во всех точках рассматриваемого пространства с учетом времени звукового воздействия. Из соотношения (6.26) следует

L^L-L, (6.42)

Референтные значения звукового давления, интенсивности и им-педанса равны: а = 2 • 10'⁵ Па, 1 = 10¹² Вт/м² = 400 Па • с/м.

Характеристический импеданс среды для звука равен произведению скорости звука в среде сна ее плотность p:z = рс. Для атмосферного воздуха при р == 1,29 кг/м³ и с = 331 м/с ^ = 430 кг/(м² • с). В табл. 6.8 приведены значения импеданса г для разных сред.

 

Таблица 6.8. Плотность, скорость звука и характеристический импеданс для некоторых сред и материалов

Среда, материал	Плотность ρ, кг/м^3	Скорость звука с, м/с	Импеданс z= рс, Па∙ с/м
Водород	0,084
Вода			1,45 • 10^6
Бензин			0,89 • 10^6
Алюминий			16,5 • 10^6
Медь			41,1 • 10^6
Сталь			47,6 10^6
Стекло		4900...5900	(12...15) • 10^6
Полистирол			2,94 • 10^6
Железобетон			11•10^6
Кирпич			4,1 • 10^6
Пробка			0,12∙10^6
Резина (техниче			0,72 • 10^6
ская)

При распространении звука в атмосфере значение импсданса будет зависеть от температуры и давления. Значение ^ = 400 Па • с/м будуг соответствовать условиям, когда, например, давление и температура будут соответственно равны 0,9 • 10⁵ Па (675 мм рт. ст.) и –27 °С или 1,013 • 10¹⁵ Па и +38,8 °С. Однако при изменении давления и температуры в пределах обычной атмосферы уровень импеданса 2^= lOlg^* незначителен и им пренебрегают, полагая, что Lp(f) = Z//).

Уровень интенсивности или плотности потока энергии можно определить, используя зависимости (6.29), (6.30), (6.33).

Для расчета уровня шума в изолированном объеме используют уравнение (6.33), которое записывают в децибелах в виде

Рис. 6.41. Схема расчета уровня шума в изолированном объеме

 

де Z/„(г, В) – уровень плотности потока энергии на сферической поверхности радиуса г, образованной телесным углом излучения Q при данном значении постоянной изолированного объема B=aS/(l– а), где S– общая площадь его внутренней поверхности с коэффициентом поглощения а; ^5 – затухание звука (см, пояснения к формуле (6.29), которое в большинстве случаев можно принять равным нулю, S(r) == 4пу^. Сферическая поверхность описывается радиусом г из акустического центра (АЦ). Если источник расположен на плоскости (и = 2п), то АЦ совпадает с проекцией геометрического центра источника на эту плоскость. Угол излучения Q зависит от местоположения источника шума: и = 2тс при расположении источника на плоско-ста; П = я – в двухгранном угле; Q == я/2 – в трехгранном угле, образованном ограждающими стенками. При отсутствии более точных данных углу О соответствует коэффициент направленности ф = (W/ ^)/(W/4nr¹) = 4w/Q.

Формулу (6.43) обычно применяют, коща радиус г > 24пах> гае ^пях – максимальный размер источника.

Чтобы определить уровень шума в точке ^изолированного объема (см. рис. 6.41), в формуле (6.43) следует положить r= /\i. Найденное таким образом значение L^ сравнивают с нормами.

В выражение (6.43) входит коэффициент поглощения а, который зависит от многих факторов, например, от угла падения и частоты. На практике при расчетах по формуле (6.43) используют значения коэффициентов поглощения, полученные при измерениях в трубе или в реверберационной камере, несмотря на то, что их значения могут различаться (например, теоретически при измерениях в трубе а <, 0,95, а для того же случая в реверберационной камере а = 1,2). В практических расчетах коэффициент а вычисляют по правилу: для частот/== 63... 1000 Гц принимают а == ао, где ао определяют по табл. 6.9; для частот /= 2000...8000 Гц коэффициент а вычисляют по формуле: а = «1–(1–oio)exp(–25/), ще 6 в нужной размерности находят из табл. 6.7, а постоянная

л

затухания звуковой энергии в объеме Н равна 1= 4 V/ Si.

Таблица 6.9 Коэффициент поглощения а в производственных помещениях

Тип помещения	Среднегеометрическая частота, f, Гц
Машинные за-	0,07	0,08	0,08	0,08	0,08	0,08	0,09	0,09
лы, испытатель-
ные стенды
Механические	0,10	0.10	0.10	0,11	0,12	0.12	0,12	0,12
и металлообраба-
тывающие цехи;
цехи агрегатной
сборки в авиа- и
Судостроительной
Промышленности
Цехи деревооб-	0,11	0,11	0,12	0,13	0,14	0,14	0,14	0,14
работки, посты
управления, ла-
боратории, кон
структорские
бюро

 

Некоторые ориентировочные значения коэффициента поглощения даны в табл. 6.9. Если стенки изолированного объема изготовлены из п разных материалов, то в выражении (6.43) а есть среднее значение коэффициента звукопоглощения:

где Wf – усредненный за период поток энергии, падающий на поверхность /-стенки, площадь и коэффициент поглощения которой соответственно равны *У/ и a/; Sa == ^ а/*У/ – эквивалентная площадь i - внутренней поверхности изолированного объема (i = 1, п).

Из уравнения (6.32) следует, что степень диффузного поля может быть охарактеризована отношением 41д//= ^с. Пространство, где ^ < 1 (т. е. вблизи источников шума), называют зоной прямого звука, а пространство, где ^ > 1 (т. е. вдали от источников, вблизи стенок изолированных объемов),– зоной отраженного звука. Условие % = 1 позволяет^задать границу между этими зонами в виде радиуса г, = = ^Вф/(16пг¹) (см. рис. 6.41) и при г» г^ записать выражение (6.43) в виде (^а=0):

lj (г, В) - L(В) = Z.+ ioig(4.y / В). (6.44)

Звукопоглощение. Для уменьшения отраженного звука применяют защитные устройства, обладающие большими значениями коэффициента поглощения, к ним относятся, например, пористые и резонансные поглотители.

Звуковые волны, падающие на пористый материал, приводят воздух в порах и скелет материала в колебательные движения, при которых возникает вязкое трение и переход звуковой энергии в теплоту. Коэффициент звукопоглощения а будет зависеть как от угла падения звуковых волн, так и от частоты. Для пористого поглотителя, находящегося на жесткой стенке, частотная характеристика коэффициента а имеет вид, показанный на рис. 6.42, д. Для усиления звукопоглощения на низких частотах между пористым слоем и стенкой делают воздушную прослойку (рис. 6.42, б). Пористые поглотители изготовляют из органических и минеральных волокон (древесной массы, кокса, шерсти), из стекловолокна, а также из пенопласта с открытыми порами. Для защиты материала от механических повреждений и высыпаний используют ткани, сетки, пленки, а также перфорированные экраны. Последние существенно изменяют характер поглощения звука защитным устройством (рис. 6.42, в).

Резонансные поглотители имеют воздушную полость, соединенную отверстием с окружающей средой. Воздух в резонаторе выполняет роль механической колебательной системы, состоящей из элементов массы, упругости и демпфирования. Если пренебречь рассеиванием звуковой энергии, то импеданс резонатора, равный механическому импедансу (см. формулу (6.18), отнесенному к единице площади, будет равен нулю на частоте со. При импедансе резонатора ^ = 0 коэффициент отражения звукового давления R = –1. Таким образом, снижение шума происходит за счет взаимного погашения падающих и отраженных волн.

Рис. 6.42. Частотные характеристики коэффициента поглощения:

а –для пористого поглотителя на жесткой стенке; б– для пористого поглотителя с воздушной прослойкой; в – при наличии перфорированного экрана; г –для резонансного поглотителя, образованного перфорированным экраном

 

Резонансным поглотителем является также перфорированный экран с отверстиями, затянутыми тканью или мелкой сеткой (рис 6.42, г), который существенно меняет характер поглощения. Пористые и резонансные поглотители крепят к стенкам изолированных объемов.

Кроме того, звукопоглощение может производиться путем внесения в изолированные объемы штучных звукопоглотителей, изготовленных, например, в виде куба, которые в производственных помещениях чаще всего подвешивают к потолку.

К хорошим звукопоглощающим материалам относят те, которые на среднегеометрических частотах октавных полос 250, 500, 1000, 2000 Гц имеют коэффициент а, равный или превышающий соответственно значения: 0,2; 0,3; 0,4; 0,5.

Обозначив постоянную изолированного объема до установки поглощающих материалов через Д== (х-5/(1–а), а после установки – В == аД(1 –а) и записав коэффициент защиты в виде: kw = In(r, B)/In{r, В), найдем эффективность звукопоглощения:. /

е = lOlgA^ = L^ (г. В) – Zi„(r, В), (6.45)

где уровни Z/„ (r,B) и L^ (r, В) оп^юделяют по формуле (6.43).

Для вычисления постоянной В имеет смысл коэффициент а выразить через площадь 5», на которой предполагается разместить защитные

устройства со средним коэффициентом звукопоглощения, равным о». Эквивалентная площадь внутренней поверхности изолированного объема до установки защитных устройств Дх == а*У== а'(*У–А)4- + a"S^ где а' и а" – средние коэффициенты звукопоглощения поверхностей площадью (S– iS») и S^ эквивалентная площадь после установки защитных устройств Sa ^dS^a^S–S^) + а^. Из этих уравнений находим а == а– (а" – a^S^/Su в тех случаях, когда можно принять aS a"S^ имеем а = Sa(*)/S, где *Уа(*) = = а^ – эквивалентная площадь звукопоглощающих устройств. При внесении в изолированные объемы штучных звукопоглотителей &(*)= ос^ + ^ Sa.(i)fii, где Sa(i} I – экивалентная площадь /-то звукопоглотителя, а/г/ – их число. И < выражений (6.44) и (6.45) видно, что эффективность е в зоне отраженного звука удобно вычислять по формуле:

e=lOig£/R

Требуемая эффективность звукопоглощения определяется по формуле (6.43), исходя из условия безопасности: L//r, В) ^ L». Однако следует учитывать, что практическая реализация звукопоглощения позволяет снижать шум обычно не более чем на б... 8 дБ (в зоне отраженного звука –на 10... 12 дБ).

Звукоизоляция. Звукоизоляция– уменьшение уровня шума с помощью защитного устройства, которое устанавливается между источником и приемником и имеет большую отражающую и (или) поглощающую способность. Обычно роль защитных устройств выполняют глушители шума, экраны или стенки изолированных объемов. Например, защитным устройством является кожух, которым закрывают машины и механизмы, или кабина, в которой находится оператор, управляющий рабочим процессом. Стенки кожухов и кабин изготовляют из листового проката и покрывают изнутри звукопоглощающим материалом. Эффективность звукоизоляции с помощью стенки толщиной h можно определить по формуле (6.39). Если пренебречь затуханием звука в материале, т. е. положить в формуле (6.39) коэффициент распространения А» равным jka, где kz = со/Сз – волновое число, то эффективность

е = 1 Olg[cos²^ 4- 0,25feAi + Zi/^ )²sm²^2A], (6.46)

где Zi ⁼⁼ pi^i – импеданс воздуха; ^ = рзСз – импеданс материала защитного устройства.

Из выражения (6.46) следует, что эффективность звукоизоляции равна нулю при толщине стенки А==/г^2/2, т. е. кратной половине длины волны (п= 0, 1, 2...), а максимальная эффективность будет иметь место, если толщина стенки h = (2п + 1)Х2/4.

Так как для защитного устройства, находящегося в воздухе, всегда выполняется неравенство piCi «рдОг, то для тонкой стенки (h^ « ^2/271) из выражения (6.46) находим

^=101g[l+(wo)/2pici)²], (6.47)

где т == рзА – поверхностная плотность (масса защитного устройства, отнесенная к единице площади).

При достаточно больших частотах единицей в правой части формулы (6.47) можно пренебречь:

е = 20 Ig-^ = 20 lg(w/)–const. ^(6M) 2piCi

Как видно из формулы (6.48), единственным свойством защитного устройства, определяющим эффективность звукоизоляции при принятых допущениях, является поверхностная плотность т. Эффективность звукоизоляции растет с увеличением плотности т и частоты / Константу, входящую в выражение (6.48), определяют, осредняя коэффициент передачи т по углам падения. Если т и / выражены соответственно в кг/м² и Гц, то константа равна 47,5 дБ.

Найдем требуемую эффективность звукоизоляции. По определению

<?= 10 lgl/т == 10 IgW^/y = Lw^–Lw. (6.49)

Будем обозначать параметры, относящиеся к изолированному объему, в котором установлен источник шума мощностью W, индексом 1, а параметры, относящиеся к изолированному объему, где расположен приемник, индексом 2. Суммарная плотность потока энергии t звука, падающего на ограждающие стенки изолированного объема 1, в общем случае складывается из интенсивности W/[S\(r)} прямого звука и плотности потока энергии ^ = wib\ диффузного поля

Обозначая через S^ площадь поверхности тех стенок изолированного объема 1, через которые звук излучается в изолированный объем 2, находим падающий поток энергии W^ = -/У и с учетом выражения (6.50) имеем:

Допустимый уровень Lw"– потока энергии, переданного в изолированный объем, находим из выражения (6.43), полагая 1^(г, В) ^ L^ (e^O)

| Lw ^ zh–io ^[фА/ад + 45^]. (6.52)

Подставив соотношения (6.49) и (6.51) в формулу (6.52), получим значение требуемой эффективности звукоизоляции:

Для точечного источника шума, находящегося в изолированном объеме 7, образованным стенками кожуха (рис. 6.43, а), и излучающего шум в изолированный объем 2 (например помещение), можно в первом приближении принять S^ = 5'i(r)= 5p Тогда из выражения (6.53) требуемая эффективность

На рис. 6.43, б показано помещение 7, в котором установлен источник шума, отделенное от помещения 2 где расположены рабочие места, стенкой, площадь которой равна 5. Принимая, что в помещении 2 уровень шума во всех точках примерно одинаков (т. е. 2?2/(452(г)) «1), из выражения (6.53) находим

где радиус г равен минимальному расстоянию от акустического центра источника шума до стенки площадью *У\ На рис. 6.43, в показана кабина, защищающая оператора от шума, создаваемого источником в помещении 7. Если кабина расположена на большом расстоянии от источника, то она находится в зоне отраженного звука. Для этого источника из выражения (6.53) находим, что требуемая эффективность

Р и с. 6.43. Схемы снижения шума:

а –изолирующим кожухом; б– звукоизолирующей перегородкой; в –с помощью звукоизолирующей кабины

Рис. 6.44. Схема снижения шума экраном

 

При установке экрана между источником и приемником (рис. 6.44) за экраном образуется звуковая тень. Уровень шума в теневой зоне от точечного источника