Многолучевая интерференция. Коэффициент отражения. Формулы Эйри.

Ø Многолучевая интерференция

Многолучевая интерференция – участие в интерференции более 2 когерентных лучей.

В случае многолучевой интерференции по сравнению с двухлучевой происходит резкое увеличение яркости светлых интерференционных полос с одновременным уменьшением их ширины.

Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления, нанесенных на отражающую поверхность.

Коэффициент отражения - отвлеченное число, показывающее отношение светового потока, отраженного телом, к световому потоку, падающему на него: ρ=F/F 0.

Так как в природе не существует таких тел, которые полностью отражали бы весь падающий на них световой поток, и все тела в той или иной мере поглощают свет, коэффициент отражения всегда меньше единицы.

Коэффициенты отражения:

· Правильного (зеркального) отражения

· коэффициент диффузного отражения

· общий коэффициент отражения.

Коэффициент отражения R от полированной стеклянной поверхности зависит от показателя преломления стекла и от угла падения луча.

Рис. Зависимость коэффициента отражения от угла падения луча на поверхность раздела воздух - стекло

для углов до 45-50°, т. е. в пределах того, что имеет место в обычных объективах, коэффициент отражения остается практически постоянным и, следовательно, зависит только от показателя преломления стекла.

Значение R может быть вычислено по формуле:

где n - показатель преломления стекла.

Коэффициент отражения растет с увеличением показателя преломления. Этим объясняются большие потери света, имеющие место в сложных объективах, изготовленных из тяжелых сортов оптического стекла, если их поверхности не просветлены.

Формулы Эйри.

· Формула для прошедшей волны

Предположим, что на пластинку падает под углом плоская монохроматическая волна с амплитудой E ₀. При нахождении комплексной амплитуды суммарной волны, прошедшей через пластинку, нужно учесть, что фаза каждой последующей волны больше фазы предыдущей на

где - волновое число. Поэтому комплексная амплитуда последующей волны отличается дополнительным множителем от амплитуды предыдущей. В результате комплексная амплитуда всей прошедшей волны представится геометрической прогрессией:

Мы считаем здесь размеры пластинки и линзы достаточно большими, чтобы можно было не учитывать дифракцию на их краях и виньетирование наклонных пучков (т.е ограничение их поперечного сечения краями пластинки и линзы).

Для нахождения интенсивности прошедшей волны умножим E ₂ в формуле на комплексно-сопряженную величину и воспользуемся формулами для энергетического коэффициента отражения:

Таким же способом легко получить выражения для амплитуды и интенсивности отраженной волны.

 

· Формула для отраженной волны

Тем же способом, каким мы получили выражение для амплитуды прошедшей волны, легко получить выражение для амплитуды отраженной волны:

Здесь учтено, что . Для интенсивности отраженной волны находим

 

 

· Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.

· Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно.

· Метод зон Френеля (строим волновую поверхность, на ней отмечаем границы зон - они удалены от точки экрана на полуцелое число длин волн. Если таких зон четное число, в точке экрана освещенность 0, если нечетное - освещенность положительная).

· Зонная пластинка — плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. Зонная пластинка «выключает» чётные либо нечётные зоны Френеля, чем исключает взаимную интерференцию (погашение) от соседних зон, что приводит к увеличению освещённости точки наблюдения. Таким образом зонная пластинка действует как собирающая линза.

 

· Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия.

Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами,

 

где, знак плюс соответствует нечетным m, минус - четным m.

 

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А₁, т.е.вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное - то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на вне осевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то A_{m ≪} A₁и результирующая амплитуда A = A₁/2,т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

· Теорема Бабине (в теории дифракции) – теорема, согласно которой Фраунгоферовы дифракционной картины от каждого из дополнительных экранов, получаемые в фокальной плоскости линзы, одинаковы для любой точки, за исключением самого фокуса.

 

14 Вопрос Дифракционная решетка как спектральный прибор Дифракционная решетка - представляет собой совокупность большого числа находящихся в одной плоскости узких, параллельных, близко расположенных друг к другу прозрачных для света участков (щелей), разделенных непрозрачными промежутками. С помощью дифракционной решетки можно производить очень точные измерения длины волны. Если период решетки известен, то определение длины волн сводится к измерению угла θm, соответствующего направлению на выбранный максимум m-го порядка.С увеличением числа щелей растет интенсивность главных максимумов, ибо возрастает количество пропускаемого решеткой света. Но самое существенное изменение, вызванное большим количеством щелей, состоит в превращении расплывчатых главных максимумов в резкие, узкие максимумы. Резкость максимумов дает возможность отличить близкие длинны волн, которые изображаются раздельными, яркими полосками и не будут перекрывать друг друга, как это имеет место при расплывчатых максимумах, получающихся при одной или малом количестве щелей. Измерение длины световой волны при помощи дифракционных решеток принадлежит к числу наиболее точных. Постоянная решетки Дифракционные решетки бывают отражающие и пропускающие свет. Принцип их действия одинаков. Решетку изготовляют с помощью делительной машины, наносящей периодические параллельные штрихи на стеклянной или металлической пластине. Хорошая дифракционная решетка содержит до 100 000 штрихов. Обозначим: a - ширина прозрачных для света щелей (или отражающих полос); b - ширина непрозрачных промежутков (или рассеивающих свет участков). Величина d = a + b называется периодом (или постоянной) дифракционной решетки. Разрешающая способность Разрешающей способностью спектрального прибора принято называть отношение где – минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с близкими значениями и считаются разрешенными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии. Рис. поясняет критерий Рэлея. Так как спектральные линии, изображенные на рис. некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея. 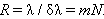    Порядок спектра Решетка способна разлагать свет в спектр. Для этого могут быть использованы дифракционные максимумы различных порядков (кроме m = 0). Практически, однако, используются главные максимумы, расположенные в пределах основного лепестка диаграммы излучения одиночной щели, имеющего полуширину . Т.е макс порядок спектра Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3. Правило Релея Условие Δl = r называют критерием разрешения Релея расстояние Δl между центрами дифракционных изображений r центрального светлого пятна Угловая дисперсия По определению, угловой дисперсией D называется величина: δ - знак дифференциала. d - обозначает постоянную решетки. В определении угловой дисперсии δλ - разность длин волн двух соседних линий, δφ - соответствующая разность углов, под которыми наблюдаются главные максимумы. Линейная дисперсия где l - расстояние вдоль экрана наблюдения, δl - расстояние между линиями на экране. 15 Вопрос Дифракция на пространственной решетке Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат. Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной. Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток: и где φ - угол между направлением на главный максимум (направление луча) и нормалью к решетке; m – порядок дифракционного максимума. Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос. Условия максимума для трехмерной решетки Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов: , (m = 1, 2, 3,....). Из формулы видно, что дифракция будет наблюдаться лишь при. Т. е. при условии будут отсутствовать дифракционные максимумы. Поэтому условие называют условием оптической однородности кристалла. Из формулы следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу. 16) Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества. формула вульфа-брега. 2dsin(a) = nl l - длинна волны. a – угол «скольжения», угол между направлением пучка, и «поверхностью кристаллической решетки» n – 1,2,3,.... Рентгенография — исследование внутренней структуры объектов, которые проецируются при помощи рентгеновских лучей на специальную плёнку или бумагу. 17) Голография — набор технологий для точной записи, воспроизведения и переформирования волновых полей. 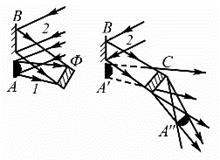схема получения объемных голографических изображений. Суть этого метода состоит в следующем: c помощью фотопластинки Ф (рис. 3.8) регистрируется интерференционная картина, возникающая при наложении волны 1, рассеянной объектом А (так называемой предметной волны), и когерентной ей волны 2, имеющей фиксированные значения амплитуды и фазы. Волна 2 называется опорной волной (опорным пучком). Она испускается тем же источником света, который освещает объект А, и после отражения от зеркала В падает непосредственно на фотопластинку Ф. Интерференционную картину, зафиксированную на фотопластинке после ее проявления, называют голограммой объекта. Для восстановления изображения голограмма С помещается в то же самое положение, где она находилась до регистрации. Ее просвечивают, как диапозитив, той же опорной волной 2, которая использовалась для получения голограммы. Однако вторая часть опорного пучка перекрывается диафрагмой. Падающая световая волна дифрагирует на голограмме. В результате дифракции наблюдаются два объемных изображения объекта: мнимое и действительное. Мнимое изображение A' находится в том же месте по отношению к голограмме, где помещается объект А при съемке голограммы. Действительное изображение A'' располагается по другую сторону голограммы. Оно имеет рельеф, обратный рельефу предмета, что создает определенные неудобства. Обычно пользуются мнимым голографическим изображением, которое по зрительному восприятию тождественно самому предмету.

 

 

Источник: http://page-book.ru/i320312

Детлаф А.А. Яворский Б.М. Курс физики. Том III Волновые процессы. Оптика. Атомная и ядерная физика (стр. 188-191)