
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютно упругий удар шаровСодержание книги
Поиск на нашем сайте
Рассмотрим абсолютно упругий удар шаров, при котором происходит упругая деформация шаров, не возникает тепла и пластической деформации (рис.8.3). Даны массы шаров и их скорости до удара Пусть В такой ситуации должны выполняться законы сохранения импульса и механической энергии. Запишем эти законы применительно к данному случаю, причем закон сохранения импульса представим в алгебраической форме:
Перепишем эти формулы следующим образом:
Разделим (8.48) на (8.47) почленно:
Теперь имеем систему линейных уравнений (8.47) и (8.49). Для нахождения скоростей шаров после взаимодействия
Откуда
В системе уравнений (8.46) ничего не изменится, если заменить индекс 1 на индекс 2, поэтому для получения формулы, выражающей
В общем случае
Знак (+) соответствует случаю, когда первый шар нагоняет второй, а знак (-) - когда шары движутся навстречу друг другу. Из уравнения (8.53) видно, что: 1) если m1 = m2 = m, то u1 = v2, а u2 = v1, т.е. в этом случае шары обмениваются скоростями; 2) при ударе шара о стенку (m2>>m1): а) u2 = v2 - скорость стенки остается неизменной; б) u1 = 2v2 – v1 - при этом, если стенка неподвижна (v2 = 0), скорость шара после удара, оставаясь неизменной по величине, изменяет свое направление на противоположное. При v2 = 0 u1 возрастает до 2v2 при движении стенки навстречу шару и убывает до 2v2, если стенка удаляется от него. Лекция 9. Основы релятивистской механики. Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования. Закон сложения скоростей в классической механике. Представления о свойствах пространства и времени в специальной теории относительности. Постулаты специальной теории относительности. Преобразования Лоренца для координат и времени. Следствия из преобразований Лоренца: сокращение движущихся масштабов длин, замедление движущихся часов, закон сложения скоростей.
9.1. Принцип относительности Галилея. Теория относительности, физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физических процессов. Универсальность пространственно-временных свойств, рассматриваемых теорией относительности, позволяет говорить о них просто как о свойствах пространства-времени. Наиболее общая теория пространства-времени называется общей теорией относительности (ОТО) или теорией тяготения, так как согласно этой теории свойства пространства-времени в данной области определяются действующими в ней полями тяготения. В специальной (частной) теории относительности (СТО), основы которой были опубликованы А. Эйнштейном в 1905 г., изучаются свойства пространства-времени, справедливые с той точностью, с какой можно пренебрегать действием тяготения. Таким образом, логически СТО - частный случай ОТО; исторически построение ОТО А. Эйнштейном было завершено в 1915 году, после чего и появился термин "частная (специальная) теория относительности". Надо отметить, что еще до появления СТО голландский и французский физики Лоренц и Пуанкаре были близки к получению результатов, вытекающих из положений СТО. А. Эйнштейн представил с единой точки зрения все известные до него эксперименты по определению скорости света и зависимости скорости распространения света от того, движутся или нет источники и приемники света, изложил физическое понимание проблем, с которыми столкнулись электродинамика и оптика. Рассматривая движение материальных точек (тел) в классической механике, предполагается, что они движутся со скоростями v<<c (v - скорость движущегося объекта; c - скорость распространения света в вакууме). Говоря о механическом движении, т.е. о перемещении тела в пространстве, всегда имеется в виду его движение относительно других тел (или одних частей тела относительно других его частей). Для математического описания движения тел с этим телом и другими телами жестко связывается система отсчета и часы для определения времени. Положение материальной точки (тела) в выбранной системе отсчета определяется либо с помощью координат (X,У,Z), либо с помощью радиус-вектора r и часов. При движении материальной точки (тела) в инерциальной системе отсчета предполагается: 1) выбранная система отсчета неподвижна или движется равномерно и прямолинейно относительно любой другой инерциальной системы отсчета; 2) условия движения тела в различных системах отсчета одинаковы; 3) основное уравнение динамики F = d p /dt = m a (второй закон Ньютона) справедливо, если наблюдатель неподвижен относительно выбранной системы отсчета. В этом случае: 1) тело, брошенное вдоль вагона, достигает противоположной стенки за одно и то же время, независимо от того движется ли оно по направлению движения поезда или в противоположном направлении, причем это время такое же, как и в покоящемся вагоне; 2) тело, брошенное вертикально вверх в вагоне, движущимся равномерно и прямолинейно (движущейся системе отсчета), вернется в ту же точку вагона, из которой оно было брошено, а не отклонится в сторону, противоположную направлению движения вагона; 3) упругий удар биллиардных шаров в обеих инерциальных системах (покоящейся и движущейся) отсчета заканчивается разлетом на одинаковые углы и с одинаковыми скоростями, если только в двух системах отсчета были одинаковые начальные скорости и направления движения.
Все это показывает, что в классической механике справедлив следующий закон природы: "В двух системах отсчета, движущихся друг относительно друга равномерно и прямолинейно, все механические явления протекают одинаково (при одинаковых условиях)". Это положение, сформулированное еще Галилеем, получило название классического принципа относительности, или принципа относительности Галилея. Если начальные условия в различных системах отсчета не одинаковы, то величины, характеризующие движение (координаты, скорости, траектория движения), относительны. Например, траектория движения тела, свободно падающего вертикально вниз в неподвижной системе отсчета, представляет собой прямую линию. Однако по отношению к движущейся системе отсчета это же тело движется по параболе. Наблюдая движение тел внутри инерциальных систем отсчета, нельзя установить, какая из них движется, а какая покоится. Это позволяет придать принципу относительности Галилея другую (отрицательную) формулировку: "Никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами (представляющими собой совокупность пружин, нитей, блоков, рычагов и т. д.), не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета.
Согласно механическому принципу относительности, во всех инерциальных системах отсчета законы классической механики имеют одинаковую форму. Рассмотрим две инерциальные системы отсчета: систему К, которую будем считать условно неподвижной, и систему К', движущуюся относительно К равномерно и прямолинейно со скоростью v0 (v0 = const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадали. В классической механике предполагается, что время не зависит от относительного движения систем отсчета (рис.9.1). Положение произвольной точки в этих системах можно определить радиус-векторами r и r '; положение начала координат системы К' в системе К - радиус-вектором r o. Если направление скорости v 0 совпадает с направлением r o, то в произвольный момент времени t, положение выбранной точки в системе К можно определить так:
r = r '+ r 0= r '+ v ot; t = t'. (9.1) В проекциях на оси координат выражение (9.1) будет иметь следующий вид: x = x' + v0xt, у = у' + v0уt, z = z' + v0zt, t = t'. (9.2) Соотношения (9.2) называют обратными преобразованиями координат Галилея. Для получения прямых преобразований Галилея необходимо поменять знак относительной скорости v0. В результате получим x' = x - v0xt, у' = у - v0уt, z' = z - v0zt, t = t'. (9.3) Или в векторной форме r' = r -v0t; t = t'. (9.4) Уравнения, обе части которых при переходе от одной системы координат к другой преобразуются одинаково и благодаря этому сохраняют свой вид во всех координатных (инерциальных) системах, называются ковариантными или инвариантными по отношению к рассматриваемому преобразованию координатных систем. Поэтому уравнения, выражающие физические законы в векторной форме, не зависят от выбора осей координат, они инвариантны. Продифференцировав (9.1) по времени, получим v = v' + v0. (9.5) Уравнение (9.5) является математической формой записи закона сложения скоростей в классической механике. Из выражения (9.5)
Таким образом, ускорение выбранной точки в инерциальных системах отсчета К и К', движущихся относительно друг друга равномерно и прямолинейно, одинаково. Следовательно, если на рассматриваемую точку не действуют внешние силы, то согласно (9.6) система К' является инерциальной (выбранная точка движется относительно нее равномерно и прямолинейно). Умножив (9.6) на массу материальной точки, будем иметь m a = m a ', (9.7) или m a = F; m a ' = F '. (9.8) Уравнения (9.8) выражают основной закон классической динамики. Равенство F = F ' означает, что законы классической динамики инвариантны при переходе от одной инерциальной системы к другой, что в свою очередь подтверждает справедливость принципа относительности Галилея. В классической механике предполагается, что время во всех инерциальных системах отсчета одно и то же (это можно доказать), а координаты выбранной материальной точки (тела) относительны. Относительные расстояния между двумя точками пространства определяются из геометрических соображений. При этом относительное расстояние между выбранными точками пространства в подвижной системе отсчета определяется соотношением
а в неподвижной системе отсчета
Сравнив (9.9) и (9.10), можно сделать вывод, что относительные расстояния в классической механике одинаковы во всех инерциальных системах отсчета, они абсолютны, т.е. инвариантны.
Таким образом, принцип относительности по своему содержанию глубоко диалектичен. Он утверждает относительность ряда величин и понятий (координаты, скорости, траектории), содержит утверждение об абсолютности (инвариантности) расстояния между телами (точками), промежутков времени между событиями, относительных скоростей тел, ускорений, об инвариантности (абсолютности) законов природы. С этой точки зрения, само название "принцип относительности" не является наиболее удачным, так как оно подчеркивает только одну, причем не самую важную сторону - относительность, и игнорирует другую - абсолютность (инвариантность) законов механики. Следовательно, можно привести математическую формулировку принципа относительности Галилея: уравнения второго закона Ньютона инвариантны относительно преобразований Галилея. Инвариантные величины (расстояния между телами (точками), промежутки времени между событиями, относительные скорости тел, ускорения) называют инвариантами преобразований. 9.2. Постулаты и представления о свойствах пространства Из механического принципа относительности Галилея следует, что скорость движения механических объектов (тел, материальных точек) относительна и зависит от того, в какой инерциальной системе отсчета происходит движение. Следовательно, скорость распространения света зависит от того, движется ли приемник или источник света или нет. Максвелл в 1878 г. предложил мысленный эксперимент по определению зависимости скорости распространения света от того, движется ли источник света или покоится. Представим вагон длиной 2l, движущийся равномерно и прямолинейно со скоростью v. В середине вагона включается лампочка S и световые лучи освещают стенки вагона. С точки зрения наблюдателя, находящегося в вагоне, лучи света достигнут передней и задней его стенки одновременно. С точки зрения наблюдателя, находящегося вне вагона, свет достигнет передней стенки вагона позже, чем задней, так как передняя стенка "убегает" от световых лучей, а задняя "догоняет" их. Это связано с тем, что если скорость света вне вагона "c" то скорость света по отношению передней стенке (c - v), а по отношению к задней стенке - (c + v). Поэтому свет должен прийти к рассматриваемым стенкам вагона в разные моменты времени. Запаздывание одного луча по сравнению с другим будет составлять
Учитывая, что v<<c, получим
откуда
Таким образом, зная длину вагона, скорость света, измерив, разность времен Dt, можно не только установить факт движения инерциальной системы отсчета, связанной с вагоном по отношению к неподвижной системе отсчета, но и найти скорость этого движения. Эту скорость естественно было бы назвать абсолютной в отличие от множества относительных скоростей по отношению к произвольно движущимся инерциальным (галилеевым) системам отсчета. Непосредственное осуществление такого эксперимента затруднительно из-за ничтожно малой разности времен Dt.
Однако такие малые разности во времени распространения света можно определить с помощью интерференционных приборов. Это связано с тем, что даже малые разности промежутков времени приводят к значительным изменениям оптической разности хода двух световых лучей: c×Dt. Определив разность хода двух лучей, рассчитав разность времен Dt, можно определить скорость v, а следовательно, и обнаружить движение одной инерциальной системы отсчета относительно другой. Многочисленные опыты (эксперименты), поставленные в разное время Майкельсоном и Морли, Томашеком, убедительно показали, что скорость света не зависит от движения источника света. Таким образом, обнаружить движение инерциальных систем отсчета относительно друг друга оказалось невозможным. В отличие от всех исследователей А. Эйнштейн усмотрел в отрицательном результате опытов Майкельсона не случайную трудность, которая нуждается в том или ином (столь же случайном) объяснении, а проявление некоторого общего закона природы: "Невозможно обнаружить прямолинейное и равномерное движение инерциальных систем отсчета по отношению к другим (к абсолютному пространству) не только механическими, но и оптическими методами". Обобщая этот результат, он выдвигает гипотезу, которая является расширением принципа относительности Галилея и носит название принципа относительности Эйнштейна (или первого постулата теории относительности): «Никакие физические опыты (механические, оптические, тепловые, электромагнитные и т.д.), производимые внутри инерциальной системы отсчета, не позволяют установить, находится ли она в равномерном абсолютном и прямолинейном движении или нет». Так же, как и принцип Галилея, принцип относительности Эйнштейна допускает и утвердительную формулировку: «Все физические явления протекают одинаково (при одинаковых условиях) в двух инерциальных системах отсчета, движущихся друг относительно друга равномерно и прямолинейно». В силу этого любая идея создания физического прибора (механического, оптического и т.п.), обнаруживающего абсолютное движение инерциальных систем отсчета, должна быть отвергнута, как и идея создания любого вечного двигателя. Принцип относительности делает совершенно надуманной и беспредметной гипотезу абсолютного пространства. Если во всех инерциальных системах, движущихся друг относительно друга равномерно и прямолинейно, все физические явления протекают одинаково. Следовательно, любую из них с одинаковым правом можно считать покоящейся абсолютно. Одновременно оказываются несостоятельными понятия абсолютного покоя и абсолютного движения. Всякое движение относительно и имеет смысл говорить лишь о движении одних тел по отношению к другим телам. Теория относительности, в основе которой лежит только принцип относительности, не может представлять физическую теорию, предсказывающую огромное количество новых фактов и имеющую колоссальное поле деятельности в современной атомной и ядерной физике. Принцип относительности представляет физическую теорию при дополнении его вторым постулатом (принципом Эйнштейна) - принципом независимости и постоянства скорости света: «Скорость света в вакууме одинакова во всех направлениях и не зависит от движения источника света». Принцип постоянства и независимости скорости распространения света подтверждается экспериментально (наблюдения за двойными звездами, опыт Томашека). С точки зрения классической физики, первый и второй постулаты теории относительности противоречат друг другу. Для устранения противоречия А. Эйнштейн предложил третий постулат - принцип одновременности событий: «События, одновременные в одной системе отсчета, не являются одновременными в другой системе отсчета, то есть одновременность является понятием относительным». Для доказательства этого постулата воспользуемся двумя инерциальными системами отсчета: неподвижной системой (К) и системой (К'), которая движется относительно (К) равномерно и прямолинейно с некоторой скоростью. Пусть в начальный момент времени координатные оси систем совпадают. Через некоторый промежуток времени у этих систем отсчета совпадают только, например, оси OX и OX' (движение системы К' происходит в направлении оси OX системы К). Если в некоторой точке В, находящейся в подвижной системе, произошла вспышка света, то свет одновременно (по часам подвижной системы) достигнет точек А и С, расположенных на одинаковом расстоянии от В. Эта вспышка света будет замечена в неподвижной системе отсчета (системе К). Так как свет распространяется с одинаковой скоростью во всех направлениях и его скорость не зависит от движения источника, то, с точки зрения наблюдателя, находящегося в системе К, свет достигнет точек А и В не одновременно. Следовательно, события, одновременные в одной системе отсчета, действительно не одновременны в другой. Из постулатов А. Эйнштейна следует, что в разных системах отсчета время разное. Поэтому допущение классической физики об абсолютном времени оказывается несостоятельным, как и представления об абсолютном пространстве. Из постулатов теории относительности вытекает тот факт, что пространство и время образуют единую пространственно-временную систему отсчета (пространственно-временной континуум). С точки зрения математики, такая система отсчета представляет собой четырехмерную систему координат. Положение материальной точки, тела в ней может быть задано с помощью четырех координат: x, у, z, и t (x, у, z, - пространственные координаты; t - координата времени, которая вычисляется по формуле: t = i∙c∙t, где c - скорость распространения света в вакууме; t - время. Известно, что расстояние между двумя точками в трехмерном пространстве определяется соотношением
В четырехмерном пространстве (в теории относительности) расстояние между двумя точками, которое называют интервалом между двумя событиями, можно определить следующим образом:
Можно показать, что интервал между двумя событиями в пространственно-временной системе отсчета всегда равен нулю (S1,2=0). Это позволяет утверждать, что интервал между двумя событиями в теории относительности инвариантен по отношению к переходу из одной системы отсчета в другую. 9.3. Преобразования Лоренца для координат и времени Формулы преобразования координат, при переходе из одной системы отсчета в другую, в теории относительности называют преобразованиями Лоренца. Для получения преобразований Лоренца выберем две инерциальные системы отсчета К и К'. Предположим, что система К' движется равномерно и прямолинейно относительно системы К со скоростью v. В начальный момент времени системы К и К' совпадали. Для любого другого момента времени расположение координатных осей систем сохраняется. При этом любая точка имеет одни и те же координаты у, z и у', z'. Координаты x и t связаны функционально: Таким образом, формулы преобразования координат можно записать в виде x = f(x', t'); у = у'; z = z'; t = F(x', t'). (9.16)
Из рисунка видно, что координата x = OA = ОВ - АВ = ОВ - МС'. OB = x'×cosj; MC' = τ'×sinj (D MC'B'); τ = AM = AA' + A'M; AA' = OC = τ'×cosφ; A'M = x'×sinφ. Следовательно, формулы преобразования координат принимают вид x = x'×cosφ - τ'×sinφ; у = у'; z = z'; τ = τ'×cosφ + x'×sinφ. (9.17) Для точек, совпадающих с началом координат (O; O'), имеем x = v×t; τ = ict; x' = 0; τ' = ict'. Подставляя значения x, τ, x', τ' в формулы преобразования, получим x = - τ'×sinφ; τ = τ'×cosφ. Разделив x на τ, имеем
Из тригонометрических соображений
Подставляя значения sinφ и cosφ в формулы преобразований с учетом τ=ict, τ' = ict', будем иметь
Полученные соотношения называют обратными преобразованиями Лоренца. Прямые преобразования Лоренца:
9.4. Следствия из преобразований Лоренца
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.34.133 (0.012 с.) |

 ,
,  . В результате такого взаимодействия вся кинетическая энергия до удара превращается в кинетическую энергию системы (шаров) после удара. В результате после удара шары будут двигаться с некоторыми скоростями u1 и u2.
. В результате такого взаимодействия вся кинетическая энергия до удара превращается в кинетическую энергию системы (шаров) после удара. В результате после удара шары будут двигаться с некоторыми скоростями u1 и u2. . Шары взаимодействуют только между собой, т.е. система замкнута, между телами действуют только консервативные силы.
. Шары взаимодействуют только между собой, т.е. система замкнута, между телами действуют только консервативные силы. . (8.46)
. (8.46) ; (8.47)
; (8.47) . (8.48)
. (8.48) . (8.49)
. (8.49) ,
,  выразим из (8.49)
выразим из (8.49)  и подставим в (8.47):
и подставим в (8.47): ,
, 
 .
. . (8.50)
. (8.50) . (8.51)
. (8.51) ; (8.52)
; (8.52) . (8.53)
. (8.53)
 Рис. 9.1
Рис. 9.1
 ; a = a '. (9.6)
; a = a '. (9.6)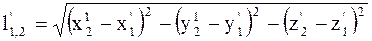 , (9.9)
, (9.9) . (9.10)
. (9.10) . (9.11)
. (9.11)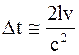 , (9.12)
, (9.12) . (9.13)
. (9.13) ;
; . (9.14)
. (9.14) (9.15)
(9.15) Формулы преобразования координат не должны изменять интервал между двумя событиями в силу его инвариантности, что возможно в том случае, когда выбранные системы отсчета равномерно вращаются относительно начала координат и относительно друг друга. В силу начальных условий положение точки М в каждой из систем отсчета может быт определено координатами М(x,t) и М(x',τ') (рис.9.2).
Формулы преобразования координат не должны изменять интервал между двумя событиями в силу его инвариантности, что возможно в том случае, когда выбранные системы отсчета равномерно вращаются относительно начала координат и относительно друг друга. В силу начальных условий положение точки М в каждой из систем отсчета может быт определено координатами М(x,t) и М(x',τ') (рис.9.2). . (9.18)
. (9.18) ;
;  .
. ; у = у'; z = z';
; у = у'; z = z';  . (9.19)
. (9.19) ; у = у'; z = z';
; у = у'; z = z'; 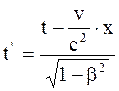 . (9.20)
. (9.20)


