
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подставив в формулу (7.83) значения R и v, будем иметь T » 92 мин.Содержание книги
Поиск на нашем сайте
Сила тяготения, действующая на космический аппарат, направленная к центру Земли, лежит в плоскости орбиты, не изменяет положение этой плоскости относительно Солнца и звезд. Если за один оборот Земли вокруг своей оси спутник делает несколько оборотов по своей орбите, то траектория движения спутника относительно Земли представляет собой ряд «витков», сдвинутых по экватору на тот угол, на который Земля успевает повернуться за один полный оборот. Под действием незначительных сил сопротивления атмосферы скорость спутника уменьшается, уменьшается радиус кривизны его траектории. Орбита оказывается не эллиптической, а представляет собой скручивающуюся спираль, в начале с малым шагом. По мере приближения к Земле сопротивление атмосферы возрастает, и шаг спирали увеличивается. Для того чтобы спутник не прекратил своего существования, проводят коррекцию его орбиты. Для возвращения на Землю космических аппаратов применяют специальные тормозные системы, резко уменьшающие их скорость, вследствие чего траектория аппарата сильно изменяется по отношению к поверхности Земли. Корабль входит в плотные слои атмосферы, происходит баллистическое торможение, и после включения двигателей мягкой посадки он совершает мягкую посадку. Имея первую космическую скорость, космический аппарат совершает движение вокруг Земли. Но этой скорости оказывается недостаточно для того, чтобы он вышел из сферы земного притяжения. Для осуществления задачи по преодолению сил земного притяжения космический аппарат должен иметь вторую космическую скорость. Значение второй космической скорости можно определить, рассчитав работу, которую необходимо совершить против сил земного притяжения для удаления космического аппарата с поверхности Земли в бесконечность. Элементарная работа, совершаемая против сил тяготения при удалении взаимодействующих масс M и m на расстояние dr, равна
Работа, совершаемая против сил тяготения при удалении массы m с поверхности Земли на бесконечность, определяется соотношением:
Эта работа должна равняться кинетической энергии, сообщаемой космическому аппарату, для придания ему скорости v2:
откуда
Если сравнить (7.82) с (7.86), то можно утверждать, что вторая космическая скорость больше первой в корень из 2-х раз. Численное значение второй космической скорости v2» 11,2×103 м/с. Известно, что впервые в мире первая и вторая космические скорости достигнуты ракетами, созданными в СССР. Так, первую космическую скорость имел выведенный на орбиту 4 октября 1957 г. искусственный спутник Земли, который имел форму шара диаметром 580 мм, массой 83,6 кг. 2 января 1959 г. был дан старт космической ракете, которая, превысив значение второй космической скорости, прошла вблизи Луны и стала первой искусственной планетой Солнечной системы. 7.7. Энергия упругой деформации При действии на систему силы упругой деформации происходит изменение конфигурации системы. В этом случае за счет работы силы упругости происходит изменение потенциальной энергии системы: dA = dWp. (7.87) Таким образом, определив работу силы упругой деформации, можно найти изменение потенциальной энергии системы, а следовательно, и энергию системы. Предположим, что сила упругости действует на некоторый стержень. В результате его длина увеличивается на некоторую величину Dl. Сила упругой деформации, в пределах выполнения закона Гука, пропорциональна удлинению стержня: F = k×Dl, (7.88) где Dl - удлинение стержня; k - коэффициент пропорциональности, численно равный силе упругой деформации, вызывающей удлинение стержня на единицу, – коэффициент упругости ( Из теории пластической деформации, сила упругости (сила упругой деформации) определяется по формуле:
где s = F/S - нормальное напряжение; S - площадь поперечного сечения стержня; E - физическая величина, численно равная нормальному напряжению, вызывающему единичное относительное удлинение стержня e (модуль Юнга); e = Dl/l - относительное удлинение. Если предположить, что стержень представляет собой некоторый куб с ребром, равным l, то работа, совершаемая силой упругой деформации по растяжению стержня на Dl, можно определить по формуле
Так как A = - DWp = Wp – W0 = Wp, то потенциальная энергия упругой деформации при продольном растяжении (или одностороннем сжатии) будет равна
Таким образом, энергия упругой деформации, в пределах выполнения закона Гука, пропорциональна квадрату удлинения стержня. Потенциальная энергия упругого сжатия будет положительна по знаку и при сжатии, и при растяжении пружины. На рисунке 7.5 представлен график зависимости потенциальной энергии пружины от ее удлинения x: 7.8. Энергия системы, совершающей колебательное движение Полная механическая энергия системы, совершающей гармоническое колебательное движение, равна сумме потенциальной и кинетической энергий системы. Изменение потенциальной энергии системы равно работе возвращающей силы, взятой с обратным знаком: DWp = - A. (7.92) Формула для определения элементарной работы возвращающей силы при изменении положения колеблющейся системы на dx имеет вид dA = F×dx×cosa = F×dx = - kx×dx. (7.93) Тогда
где x = x0 sin(ω0t + φ0) - смещение системы от положения равновесия. Следовательно, так как в положении равновесия потенциальная энергия системы W0 = 0, то в произвольном положении потенциальная энергия системы равна
|
|||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.007 с.) |

 . (7.84)
. (7.84)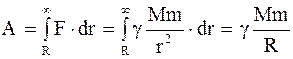 . (7.85)
. (7.85) , т.е.
, т.е.  ,
, , а
, а  . (7.86)
. (7.86)
 ).
). , (7.89)
, (7.89) . (7.90)
. (7.90) Рис.7.5
Рис.7.5
 . (7.91)
. (7.91) .
.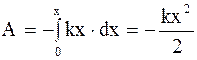 , (7.94)
, (7.94) . (7.95)
. (7.95)


