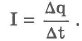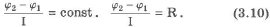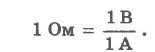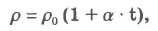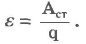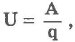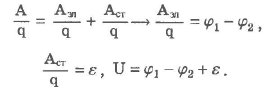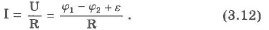Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая и потенциальная энергияСодержание книги
Похожие статьи вашей тематики
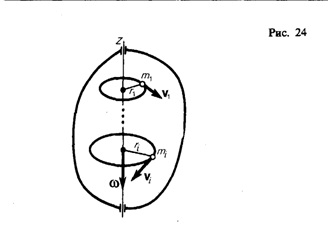
Поиск на нашем сайте В механике изучают движение и взаимодействие тел друг с другом. Поэтому принято различать два вида механической энергии: энергию, обусловленную движением тел, или кинетическую энергию, и энергию, обусловленную взаимодействием тел, или потенциальную энергию. В физике существует общее правило, связывающее энергию и работу. Чтобы найти энергию тела, надо найти работу, которая необходима для перевода тела в данное состояние из нулевого, то есть такого, при котором его энергия равна нулю. Потенциальная энергия В физике потенциальной энергией называют энергию, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела. То есть, если тело поднято над землей, то оно обладает возможностью падая, произвести какую-либо работу. И возможная величина этой работы будет равна потенциальной энергии тела на высоте h. Для потенциальной энергии формула определяется по следующей схеме: A=Fs=Fт*h=mgh, или Eп=mgh, где Eп потенциальная энергия тела, Причем за нулевое положение тела может быть принято любое удобное нам положение в зависимости от условий проводимых опыта и измерений, не только поверхность Земли. Это может быть поверхность пола, стола и так далее. Кинетическая энергия В случае, когда тело движется под влиянием силы, оно уже не только может, но и совершает какую-то работу. В физике кинетической энергией называется энергия, которой обладает тело вследствие своего движения. Тело, двигаясь, расходует свою энергию и совершает работу. Для кинетической энергии формула рассчитывается следующей образом: A = Fs = mas = m * v / t * vt / 2 = (mv^2) / 2, или Eк= (mv^2) / 2, где Eк кинетическая энергия тела, Из формулы видно, что чем больше масса и скорость тела, тем выше его кинетическая энергия. Каждое тело обладает либо кинетической, либо потенциальной энергией, либо и той, и другой сразу, как, например, летящий самолет. Формула энергии в физике всегда показывает, какую работу совершает или может совершить тело. Соответственно, единицы измерения энергии такие же, как и работы джоуль (1 Дж). абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т 1, т 2 ,..., тn, находящиеся на расстоянии r 1, r 2,..., rn от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
или
Используя выражение (17.1), получаем
где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv 2/2 ), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси. В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
где m — масса катящегося тела; vc — скорость центра масс тела; Jc — момент инерции тела относительно оси, проходящей через его центр масс; w — угловая скорость тела.
Гироско́п (от др.-греч. γῦρος «круг» и σκοπέω «смотрю») — устройство, способное реагировать на изменение углов ориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента (момента импульса) поведение гироскопа описывается уравнением:
где векторы Отсюда следует, что момент силы
то есть Прецессия гироскопа Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы. Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии. С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем. В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно. Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике —теорема Пойнтинга. С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени. Философское значение закона. Открытие закона сохранения энергии оказало влияние не только на развитие физических наук, но и на философию XIX века. С именем Роберта Майера связано возникновение так называемого естественно-научного энергетизма — мировоззрения, сводящего всё существующее и происходящее к энергии, её движению и взаимопревращению. В частности, материя и дух в этом представлении являются формами проявления энергии. Главным представителем этого направления энергетизма является немецкий химик Вильгельм Оствальд, высшим императивом философии которого стал лозунг «Не растрачивай понапрасну никакую энергию, используй её!»
Закон сохранения и превращения энергии является одним из важнейших законов природы. Закон сохранения и превращения энергии является одним из фундаментальных законов природы и может быть сформулирован так: во всех процессах, происходящих в природе, энергия не исчезает и не создается, а переходит от одного тела к другому и превращается из одного вида в другой в эквивалентных количествах.
Закон сохранения и превращения энергии имеет глубокий философский смысл. Он блестяще подтверждает одно из основных положений диалектического материализма о том, что движение является неотъемлемым свойством материи, что оно несотворимо и неуничтожимо, а лишь преобразуется из одних форм в другие. Закон сохранения и превращения энергии строго выполняется в любых физических процессах, происходящих в природе и технике. В любом потребителе энергия переменного тока не исчезает, а лишь превращается из одной формы в другую в равной количественной мере. С помощью электродвигателя переменного тока происходит преобразование энергии электромагнитных колебаний в механическую энергию, а в лампах накаливания, в спиралях электрических плит и электрических печей электрическая энергия переменного тока преобразуется во внутреннюю энергию нагреваемых тел.
5. Внутренняя энергия включает в себя энергию всевозможных видов движений внутри системы и энергию взаимодействия всех нее частиц. Из формулы (2.2.11) Любая энергия передается в виде двух форм: теплоты и работы. Если энергия передается на молекулярном уровне, то есть в ее передаче участвуют мельчайшие частицы вещества, то это будет передача энергии в форме теплоты. Количество энергии, передаваемое при тепловом взаимодействии тел, называется количеством тепла. Понятие «количество тепла» обозначается Q, измеряется в
Если при передаче энергии наблюдается перемещение рабочего тела, то это передача энергии в форме работы. Полная работа обозначается L и измеряется в системе СИ в Удельная работа – есть полная работа отнесенная к массе вещества:
Теплота и работа имеют знак: если теплота подводится – положительный «+», если отводится– отрицательный «-». Работа, совершаемая системой под действием внешних сил при увеличении объема (dV>0) является положительной (работа расширения). Работа, совершаемая внешними силами над системой при уменьшении объема (dV<0) является отрицательной (работа сжатия). При l>0 работу совершает сам газ, при l<0 – окружающая среда.
6. Каждое тело имеет вполне определенную структуру, оно состоит из частиц, которые хаотически движутся и взаимодействуют друг с другом, поэтому любое тело обладает внутренней энергией. Внутренняя энергия — это величина, характеризующая собственное состояние тела, т. е. энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия одноатомного идеального газа определяется по формуле U=3/2 • т/М • RT. Внутренняя энергия тела может изменяться только в результате его взаимодействия с другими телами. Существуют два способа изменения внутренней энергии: теплопередача и совершение механической работы (например, нагревание при трении или при сжатии, охлаждение при расширении). Теплопередача — это изменение внутренней энергии без совершения работы: энергия передается от более нагретых тел к менее нагретым. Теплопередача бывает трех видов: теплопроводность (непосредственный обмен энергией между хаотически движущимися частицами взаимодействующих тел или частей одного и того же тела); конвекция (перенос энергии потоками жидкости или газа) и излучение (перенос энергии электромагнитными волнами). Мерой переданной энергии при теплопередаче является количество теплоты (Q). Эти способы количественно объединены в закон сохранения энергии, который для тепловых процессов читается так. Изменение внутренней энергии замкнутой системы равно сумме количества теплоты, переданной системе, и работы, внешних сил, совершенной над системой. D U= Q + А, где D U— изменение внутренней энергии, Q — количество теплоты, переданной системе, А — работа внешних сил. Если система сама совершает работу, то ее условно обозначают А'. Тогда закон сохранения энергии для тепловых процессов, который называется первым законом термодинамики, можно записать так: Q = Α' + D U, т. е. количество теплоты, переданное системе, идет на совершение системой работы и изменение ее внутренней энергии. При изобарном нагревании газ совершает работу над внешними силами Α' = p(V1-V2) = pΔV, где V1, и V2 — начальный и конечный объем газа. Если процесс не является изобарным, величина работы может быть определена площадью фигуры, заключенной между линией, выражающей зависимость p(V) и начальным и конечным объемом газа (рис. 13). Рассмотрим применение первого закона термодинамики к изопроцессам, происходящим с идеальным газом.
В изотермическом процессе температура постоянная, следовательно, внутренняя энергия не меняется. Тогда уравнение первого закона термодинамики примет вид: Q = А', т. е. количество теплоты, переданное системе, идет на совершение работы при изотермическом расширении, именно поэтому температура не изменяется. В изобарном процессе газ расширяется и количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы: Q = D U + А'. При изохорном процессе газ не меняет своего объема, следовательно, работа им не совершается, т. е., А = О, и уравнение первого закона имеет вид: Q = D U, т. е. переданное количество теплоты идет на увеличение внутренней энергии газа. Адиабатным называют процесс, протекающий без теплообмена с окружающей средой. Q = 0, следовательно, газ при расширении совершает работу за счет уменьшения его внутренней энергии, следовательно, газ охлаждается, Α' = D U. Кривая, изображающая адиабатный процесс, называется адиабатой.
7. Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое необходимо сообщить телу для нагревания его на один градус. Если сообщить телу количество тепла dQ, то температура тела повысится на dT градусов и его теплоемкость определится по формуле: C = dQ/dT. (10.8) Размерность теплоемкости равна [ C ] = Дж / К. Теплоемкость моля вещества называется молярной и обозначается символом Cm. Теплоемкость единицы массы называется удельной и обозначается c удили c, причем легко видеть. что Cm = mc уд. Теплоемкость произвольной массы m равна C = c уд m. Отсюда следует, что достаточно знать теплоемкость моля, чтобы рассчитать теплоемкость тела произвольной массы. Согласно первому началу термодинамики dQ = dU + dA. Отсюда следует, что количество тепла dQ, сообщенное телу при повышении его температуры на dT, будет затрачено не только от изменение внутренней энергии dU, но и на работу dA, которую газ при этом совершит. Так как процесс расширения газа на диаграмме p-V можно провести бесчисленным количеством способов, то теплоемкость газа может иметь такое же число значений. Для практических целей наиболее важными являются теплоемкость при постоянном давлении C p и постоянном объеме С v . Рассчитаем теплоемкость моля газа при постоянном объеме C vm. Первое начало термодинамики для изохорного процесса имеет вид dQ = dU m. Выражение (10.8) запишем в виде C vm = dU m /dT. (10.9) Учитывая формулу (10.2), получим C vm = i R /2, (10.10) где i - число степеней свободы движения молекул газа, R - универсальная газовая постоянная. Из выражения (10.10) следует, что теплоемкость C vm моля произвольного газа является постоянной величиной и зависит лишь от числа степеней свободы движения молекул. Следует однако заметить, что выражение (10.10) для воздуха не является справедливым при низких и высоких температурах (рис.10.4). При высоких температурах у молекул возбуждается колебательное движение и часть энергии теплового движения передается колебаниям атомов в молекуле. Число колебательных степеней свободы движения равно 2. При низких температурах, наоборот, наблюдается “замораживание” вращательных степеней свободы движения, объясняемое квантовой механикой. Поэтому зависимость теплоемкости от температуры имеет сложный вид.
C pm = dQ/dT = dU m /dT + dA m /dT, (10.11) где dA m = pdV m - работа моля газа при изменении его объема на dV m; p - давление газа. Учитывая, что pV m = RT, получим dA m = RdT. Если числен-но положить dT = 1, то dA m = R. Отсюда следует, что универсальная газовая постоянная численно равна работе изобарического расширения моля газа при его нагревании на один градус. С помощью формулы (10.9) и выражения для dA m представим равенство (10.11) в виде C pm = C vm + R, (10.12) Выражение (10.12) называется формулой Майера. Величина g = C p /C v представляет собой характерную для каждого газа величину, часто применяющуюся при расчетах. Используя уравнения (10.10) и (10.12), получим g = (i + 2)/i. (10.13) Отсюда для газа из одноатомных молекул (i = 3) получим g = 1,67; для двухтомного газа (i = 5) - g = 1,4; для трехатомного газа (i = 6) - g = 1,33.
Идеальным наз. газ у которого молекулы представляют из себя материальные точки и силы взаимодействия между ними возникают только при непосредственном взаимодействии (соударении) молекул. Давление р, температура Т и объем V, занимаемый определенной массой газа называются параметрами состояния. Каждый из параметров является функций двух других. Уравнение, связывающее р, T и V для данной массы газа называется уравнением состояния. p = f (T,V) Состояние газа однозначно определяется двумя любыми параметрами. Вместо неизмеряемого числа молекул газа N введем измеряемую величину - массу М газа. Грамм- молекула (моль) вещества- такого количества вещества, масса которого в граммах равна молекулярной массе (μ), выраженной в частях массы молекулы углерода mc ⁄ 12. Моль любого вещества содержит одинаковое количество молекул (по определению) - число Авогадро NA = 6,02 • 1023. Число молей вещества в данной массе равно: N/NA= M/μèN= M/μ*NA - число молекул в данной массе газа. pV = M/μ NAkT Произведение двух констант NA и k называется универсальной газовой постоянной. R = NAk = 8,31 [Дж/к*моль] à 8,31 • 103 [Дж/к*моль] Получим уравнение состояния идеального газа в форме Менделеева - Клайперона. pV =M/μ RT
C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <εk>хаотического движения молекул (T~<εk>). Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <εk>=3/2kT где k - постоянная Больцмана, k=1.38*10-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы. Формула позволяет выяснить смысл абсолютного нуля: T=0, если < εk > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.
Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.
Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6). В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε1>=i/2kT В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε1>=i/2kT закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы <ε>=i/2kT, где i - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=iпост +iвращ+2iколеб. В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то внутренняя энергия, отнесенная к одному молю газа, равна сумме кинетических энергий NA молекул: Функция распределения Максвела – Больцмона характеризует распределение молекул по полным энергиям
Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)3/2 V2 exp(MV2/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, градусы Кельвина, К;
Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям. Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е. Q=∆U+A В этом уравнении изменение внутренней энергии, Количество теплоты может быть положительным (Q>0), если тело получает теплоту, и отрицательным (Q>0), если тело отдает теплоту. В дифференциальной форме это запишется следующим образом δQ=dU+δA где dU и δA Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
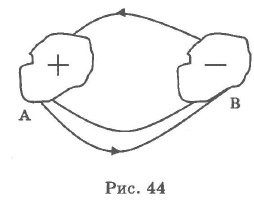
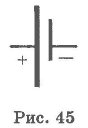
Законы Постоянного Тока До 1800 г. были построены машины, позволяющие достигать статического электричества довольно высоких потенциалов. С помощью этих машин удавалось получать сильные разряды, но практического значения они не имели. В 1800 г. произошло событие огромного значения. Алессандро Вольта (1745-1827) изобрел электрическую батарею и впервые получил с ее помощью устойчивый поток зарядов. Это открытие знаменовало начало новой эпохи, полностью преобразившей нашу цивилизацию, - вся современная электротехника основана на использовании электрического тока. Электрическим током называют упорядоченное движение электрических зарядов. В различных средах электрический ток обусловлен движением различных зарядов, но за направление электрического тока условно выбрано направление движения положительных зарядов. Постоянный ток в проводниках создается благодаря особым устройствам - источникам тока. Проводники - это такие тела, в которых имеются свободные частицы, обладающие электрическим зарядом, способные ускоряться и перемещаться под действием приложенных к ним электрических сил. Возьмем два тела, заряженных противоположными зарядами (рис. 44). Если их соединить проводником, то по нему пойдет ток. В результате выравнивания потенциалов ток прекращается.
Для того чтобы движение зарядов не прекратилось, необходимо каким-то образом положительные заряды с тела В перенести снова на тело А. Такой перенос силы электростатической природы сделать не могут. Следовательно, для поддержания тока должны существовать силы не кулоновской природы. Силы неэлектростатического происхождения, способные разделить электрические заряды, называются сторонними силами. Источник тока - это устройство, в котором происходит разделение электрических зарядов под действием сторонних сил. Сторонние силы могут быть различной природы (магнитной, химической и др.). Количественно электрический ток характеризуется силой тока. Сила тока (I) равна отношению заряда дельта q, переносимого через поперечное сечение проводника за интервал времени At, к этому интервалу времени. Сила тока - величина скалярная. При решении задач она может быть положительной или отрицательной. Знак силы тока зависит от того, какое из направлений обхода вдоль проводника принять за положительное. Сила тока I > О, если направление тока совпадает с условно выбранным положительным направлением обхода.
В Международной системе единиц силу тока измеряют в амперах (А). Эту единицу устанавливают на основе магнитного взаимодействия токов. ГОСТ 8.417-81 дает такое определение единицы силы тока: "Ампер равен силе неизменяющего тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длины 1 м силу взаимодействия, равную 2 • 10-7 Н". Немецкий физик Г. Ом в 1826 г. обнаружил, что отношение разности потенциалов между концами проводника, являющегося участком электрической цепи, к силе тока в цепи есть величина постоянная:
Эту величину R назвали электрическим сопротивлением. Единицей электрического сопротивления в СИ является ом (1 Ом). За единицу электрического сопротивления 1 Ом принято сопротивление такого проводника, в котором при разности потенциалов между его концами в 1 В течет ток силой в 1 А.
Удельное сопротивление р - величина, численно равная сопротивлению проводника длиной 1 м и поперечным сечением 1 м2. Единица удельного электрического сопротивления ом • метр (Ом • м). Для металлов и сплавов зависимость удельного сопротивления от температуры в небольшом интервале температур вблизи комнатной выражается формулой:
где р0 - удельное сопротивление при температуре t = 0 °С, а - температурный коэффициент сопротивления. Температурный коэффициент сопротивления а - величина, равная отношению относительного изменения сопротивления участка цепи к изменению его температуры, вызвавшему это изменение сопротивления. Выражение (3.10) есть закон Ома для участка цепи. Сила тока прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению R:
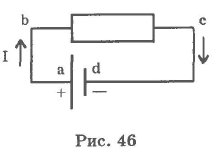
Для создания постоянного тока в цепи необходим источник тока. Условно источник тока изображен на рис. 45. Сторонние силы, разделяя электрические заряды внутри источника, создают накопление их на полюсах. Если замкнуть полюсы источника проводами с нагрузкой, то по ней потечет ток. Участок цепи abed называют внешней частью цепи, участок ad - внутренней (рис. 46).
Отношение работы, совершаемой сторонними силами при перемещении положительного заряда по всей замкнутой цепи, к значению этого заряда называется электродвижущей силой источника (сокращенно ЭДС):
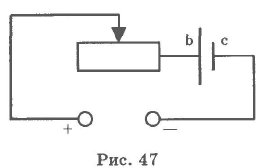
Участок электрической цепи, не содержащей источников ЭДС, называется однородным. Участок электрической цепи, который содержит источники ЭДС, называется неоднородным. В однородном участке цепи движение электрических зарядов обусловлено действием на них электрической силы. Электрическое поле, обусловливающее движение электрических зарядов в цепи, называется стационарным. Стационарное электрическое поле создается во внешней цепи зарядами полюсов источника тока и обусловливает движение зарядов в электрической цепи. Отличается от электростатического поля неподвижных зарядов тем, что оно существует внутри проводников. Примером неоднородного участка цепи является схема зарядки аккумулятора, представленная на рис. 47. В этой цепи "+" и "-" - полюса источника тока, реостат, регулирующий ток и аккумулятор (be). Участок цепи abc - неоднородный, так как содержит источник сторонних сил - аккумулятор. Уточним понятие "напряжение". За напряжение принимается физическая величина, равная отношению работы всех сил, действующих на данном участке, к значению переносимого заряда:
где А - работа всех сил, действующих на данном участке цепи (электростатических и сторонних).
Если на участке действуют только электростатические силы, то е = 0, при этом понятие напряжения и разность потенциалов совпадают. Закон Ома (3.11) можно для неоднородного участка цепи записать в виде:
Составим электрическую цепь по схеме (рис. 48). Для внешней части цепи АВ:
Внутренний участок цепи ВСА является неоднородным, следовательно, согласно (3.12):
где r - внутреннее сопротивление источника тока. Сложив оба равенства (3.13) и (3.14), получим
Формула (3.15) выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений внешнего и внутреннего участков цепи. Из формулы (3.15) следует, что если R = 0, то напряжение между полюсами уменьшается до нуля, а сила тока достигает максимального значения (короткое замыкание). Если R ~ r, то измеряя напряжение на полюсах источника, получим приближенное значение ЭДС источника. При последовательном соединении проводников общее сопротивлен
|
|||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.014 с.) |

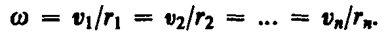 (17.1)
(17.1)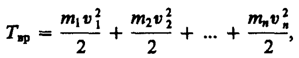
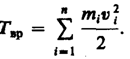
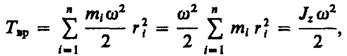
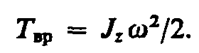 (17.2)
(17.2)
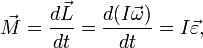
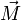 и
и 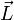 являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр
являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр 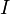 — его моментом инерции, векторы
— его моментом инерции, векторы  и
и 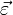 угловой скоростью и угловым ускорением.
угловой скоростью и угловым ускорением.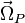 гироскопа определяется его моментом импульса и моментом приложенной силы[10]:
гироскопа определяется его моментом импульса и моментом приложенной силы[10]: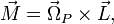
 видно, что внутренняя энергия идеального газа зависит только от его температуры, следовательно, является однозначной функцией состояния системы. Значение
видно, что внутренняя энергия идеального газа зависит только от его температуры, следовательно, является однозначной функцией состояния системы. Значение 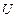 в каком-либо состоянии системы не зависит от того, каким образом система пришла в это состояние. Иначе говоря, изменение внутренней энергии
в каком-либо состоянии системы не зависит от того, каким образом система пришла в это состояние. Иначе говоря, изменение внутренней энергии 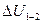 при переходе системы из состояния
при переходе системы из состояния 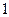 в состояние
в состояние 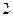 не зависит от вида процесса перехода и равно разности значений
не зависит от вида процесса перехода и равно разности значений 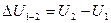 . Поэтому если в результате какого-либо процесса система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю:
. Поэтому если в результате какого-либо процесса система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю: 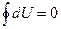 . Следовательно, элементарное изменение внутренней энергии является полным дифференциалом.
. Следовательно, элементарное изменение внутренней энергии является полным дифференциалом.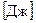 или
или 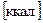 (1 ккал = 4,19 кДж). Количество теплоты, отнесенное к массе вещества, называется удельной теплотой:
(1 ккал = 4,19 кДж). Количество теплоты, отнесенное к массе вещества, называется удельной теплотой: , [Дж/кг] (1.8)
, [Дж/кг] (1.8)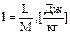 (1.9).
(1.9).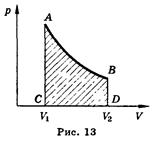
 Рассмотрим теплоемкость при постоянном давлении для моля газа. Согласно первому началу термодинамики
Рассмотрим теплоемкость при постоянном давлении для моля газа. Согласно первому началу термодинамики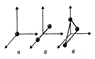 показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.
показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.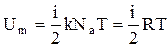 .Внутренняя энергия для произвольной массы m газа
.Внутренняя энергия для произвольной массы m газа 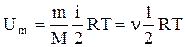 , где k - постоянная Больцмана, n -количество вещества.
, где k - постоянная Больцмана, n -количество вещества.