
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия гармонического осциллятораСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Гармонический осциллятор обладает энергией, за счёт ко-торой и совершает колебания. Найдём выражения для кинетической, потенциальной и пол-ной механической энергии идеального пружинного маятника. Кинетическая энергия
Потенциальная энергия деформированной пружины
Полная механическая энергия
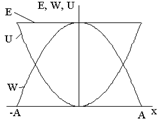
(здесь учтено, что Таким образом, полная механическая энергия идеального пружинного маятника постоянна. Кинетическая и потенциальная энергия постоянно изменяются, причём в положении равновесия кинетическая энергия достигает максимального значения, а потенциальная энергия уменьшается до нуля; при максимальном отклонении груза от положения равновесия всё наоборот – кинетическая энергия равна нулю, а потенциальная максимальна. В графической форме зависимость потенциальной, кинети-ческой и полной энергии от х имеет вид, показанный на рисунке.
Обратите внимание: что кине-тическая и потенциальная энергия изменяются с удвоенной частотой, Полученные выводы применимы не только к пружинному маятнику без потерь энергии. Полная энергия любого гармонического осциллятора определяется амплитудой колебаний и упругими свойствами осциллятора и не изменяется с течением времени. Энергия математического маятника может быть найдена из следующих соображений.
Учитывая, что при ма-лых j sinj = j, получаем
Поскольку
При возвращении маятника к положению равновесия высота груза уменьшается, при этом потенциальная энергия маятника переходит в кинетическую. В положении равновесия потен-циальная энергия уменьшается до нуля, при этом кинетическая достигает максимального значения. За счёт накопленной кинетической энергии груз продолжит своё движение и вновь поднимется на высоту h, где вся кинетическая энергия перейдёт в потенциальную. Энергия колебательного контура также может существовать в двух формах: в виде энергии, запасённой в электрическом поле конденсатора, и в виде энергии, запасённой в магнитном поле соленоида. Как показано в разд. 1.25, энергия заряженного конденсатора равна В тот момент, когда весь заряд сосредоточен на обкладках конденсатора, ток в контуре равен нулю. Вся энергия контура существует в виде энергии заряженного конденсатора. Энергия магнитного поля соленоида равна нулю. Как только конденсатор начинает разряжаться, через соленоид протекает постепенно возрастающий ток. Соответственно растёт энергия магнитного поля соленоида и уменьшается энергия заряженного конденсатора. В момент полного разряда конденсатора ток максимален. Поэтому энергия контура существует в виде энергии магнитного поля соленоида. Ток в контуре после разряда конденсатора протекает именно за счёт энергии магнитного поля. И именно за счёт этой энергии происходит перезарядка конденсатора.
Затухающие колебания
В разд. 6.4 была рассмотрена идеальная колебательная система – гармонический осциллятор. Там было показано, что полная энергия гармонического осциллятора постоянна, вследствие чего амплитуда колебаний не изменяется. В любой реальной колебательной системе существуют потери энергии (например, пружинный маятник испытывает воздействие силы трения, вследствие чего механическая энергия переходит во внутреннюю). Поскольку энергия реальной колебательной системы умень-шается, должна уменьшаться и амплитуда её колебаний. Это означает, что колебания реального осциллятора затухающие.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.006 с.) |

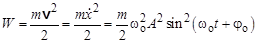 .
. .
.
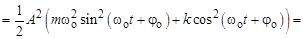
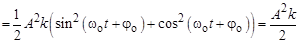
 ).
). Зависимость потенциальной, кинетической и полной энергии от времени показана на следующем рисунке (символом Т на рисунке обозначен период гармони-ческого колебания).
Зависимость потенциальной, кинетической и полной энергии от времени показана на следующем рисунке (символом Т на рисунке обозначен период гармони-ческого колебания).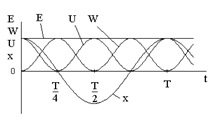 При отклонении математического маятника на малый угол j от положения равновесия груз поднимется на высоту h = l – l cosj. Потенциальная энергия маятника в этом положении равна U =
При отклонении математического маятника на малый угол j от положения равновесия груз поднимется на высоту h = l – l cosj. Потенциальная энергия маятника в этом положении равна U = 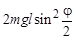 .
. .
.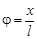 , потен-циальная энергия математического маятника может быть рассчитана и так:
, потен-циальная энергия математического маятника может быть рассчитана и так: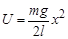 .
.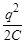 . Энергия, запасённая в магнитном поле соленоида, равна
. Энергия, запасённая в магнитном поле соленоида, равна 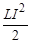 (см. разд. 5.8).
(см. разд. 5.8).


