
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Намагничивание ферромагнетика.
Этапы намагничивания
Намагничивание ферромагнетиков представляет собой про-цесс, состоящий из нескольких этапов. На первом этапе при увеличении напряжённости внешнего магнитного поля увеличиваются размеры тех доменов, у которых собственный магнитный момент образует с внешним полем острый угол. При этом уменьшается объём тех доменов, у кото-рых этот угол тупой.
______________________________
* Обычно размеры домена составляют 10-4…10-5 м. К концу первого этапа домены, у которых упомянутый угол острый, полностью поглощают те, у которых угол между собственным и внешним магнитным полем тупой. Этот этап намагничивания называют этапом смещения границ.
Второй этап намагничивания называют этапом вращения. К концу второго этапа маг-нитные моменты всех доменов направлены по внешнему магнит-ному полю. По окончании этого этапа наступает третий этап намагничивания – этап насыщения. В ходе первого и второго этапов намагничивания поле внутри ферромагнетика растёт за счёт увеличения как внешнего магнитного поля, так и магнитного поля, созданного доменами. На третьем этапе увеличение магнитного поля в ферромагнетике происходит только за счёт роста внешнего магнитного поля. Суммарное магнитное поле доменов не изменяется.
Явление гистерезиса
При уменьшении напряжённости внешнего магнитного поля до нуля, маг-нитное поле в ферромагнетике не умень-шится до нуля. Индукция магнитного поля в ферромагнетике окажется равной В ост – остаточной индукции поля в фер-ромагнетике. Другими словами – образец ферромагнетика после выключения внешнего магнитного поля останется на- Для того, чтобы уменьшить индукцию магнитного поля в ферромагнетике до нуля, необходимо изменить направление внешнего магнитного поля на противоположное и начать постепенное увеличение его напряжённости.
При некоторой напряжённости Н с индукция поля в ферромагнетике уменьшится до нуля. Эту напряжённость приня-то называть коэрцитивной силой. Дальнейшее увеличение напряжённости вызывает намаг-ничивание ферромагнетика. Направление намагничивания противоположно первоначальному. Если после намагничивания до насыщения вновь уменьшать напряжённость внешнего магнитного поля, то процесс пойдёт так, как показано на рисунке. График зависимости В (Н) замкнётся, образовав так называемую петлю гистерезиса. Само рассматриваемое явление называется явлением гистерезиса. Явление гистерезиса заключается в том, что значение В при данном Н зависит от того, какое значение Н имела ранее. Например, если ферромагнетик не намагничен, то при Н = 0 В = 0. Если ферромагнетик ранее находился в магнитном поле с Если же ранее напряжённость была отрицательной, то при Ферромагнетики делят на две группы. Основанием для клас-сификации является коэрцитивная сила. Коэрцитивная сила показывает, насколько трудно раз-магнитить ферромагнетик. Если коэрцитивная сила велика, то ферромагнетик размагнитить трудно. Такие ферромагнетики на-зывают магнитожёсткими. Из жёстких ферромагнетиков изго-тавливают постоянные магниты. Если коэрцитивная сила мала, ферромагнетик можно размагнитить, почти не затрачивая на это энергию. Такие ферромагнетики называют магнитомягкими. Из них изготав-ливают сердечники трансформаторов.
4.7. Граничные условия для векторов В и Н
Рассмотрим магнитное поле вблизи границы раздела двух сред с различной магнитной проницаемостью m1 и m2. Допустим, что магнитное поле не перпендикулярно границе раздела двух сред. Разложим векторы В и Н на две компоненты, из которых одна параллельна границе раздела двух сред, а вторая – перпендикулярна. Перпендикулярную компоненту назовём нормальной, а параллельную – тангенциальной. Начнём с рассмотрения нормальной компоненты вектора магнитной индукции Вn. Воспользуемся для этого теоремой Гаусса для магнитного поля (см. разд. 8,8).
Согласно теореме Гаусса, маг-нитный поток через замкнутую поверх-ность равен нулю. В данном случае полный маг-нитный поток через выбранную поверхность равен сумме потоков Вn через верхнее и нижнее основания и через боковую поверхность цилиндра. Поскольку высота боковой поверхности бесконечно мала, магнитный поток через неё бесконечно мал. Следовательно, полный магнитный поток равен сумме потоков через верхнее и нижнее основания. Полный магнитный поток нормальной компоненты вектора магнитной индукции равен нулю, следовательно, потоки через верхнее и нижнее основания равны между собой Bn 1D S = B n2D S. Это означает, что нормальная компонента вектора магнитной индукции на границе раздела двух сред не изменяется Bn 1 = Bn 2. По определению напряжённости В = m0m Н, поэтому m1 Нn 1 = m2 Нn 2 и
Таким образом, нормальная компонента вектора напряжён-ности магнитного поля на границе раздела двух сред изменяется. Значение нормальной составляющей напряжённости магнитного поля в средах с разной магнитной проницаемостью различно.
Выделим вблизи границы раздела двух сред замкнутый контур 1 - 2 - 3 - 4 прямоугольной формы (см. рисунок). Длина горизонтальной стороны прямоугольника равна l, а высота прямоугольника бесконечно мала. Если на границе раздела двух сред нет тока, то Компоненты циркуляции по сторонам прямоугольника, перпендикулярным границе разделы пренебрежимо малы, так как высота прямоугольника бесконечно мала. Компоненты циркуляции по параллельным сторонам соответственно равны Если длина участков 1 - 2 и 3 - 4 настолько мала, что напряжённости можно считать постоянными, то Н 1 и Н 2 можно вынести за знак интеграла. Тогда в результате интегрирования получим векторы l 12 и l 34, направление которых определяется направлением обхода контура. Таким образом, циркуляция вектора напряжённости на границе раздела двух сред оказывается равной H 1. l 12 + H 2 . l 34 = 0. Учитывая, что скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, получаем Нt 1 l – Ht 2 l = 0 (минус обусловлен тем, что векторы l 12 и l 34 противоположны по направлению). Следовательно, тангенциальная составляющая вектора напряжённости магнитного поля в средах с разной магнитной проницаемостью одинакова: Нt 1 = Ht 2. Тангенциальная составляющая вектора магнитной индукции при переходе из одной среды в другую изменяется
и
Полученные результаты означают, что силовые линии маг-нитного поля на границе раздела двух магнетиков преломляются
Из полученных результатов также следует, что если в образ-це магнетика сделать узкую щель, параллельную силовым линиям магнитного поля в ве-ществе, то напряжённость маг-нитного поля в щели будет равна напряжённости магнитного поля внутри магнетика. Это вытекает из того, что тангенциальная составляющая вектора напряжён-ности магнитного поля на границе раздела двух сред не изменяется.
Поскольку нормальная составляющая вектора магнитной индукции не изменяется на границе раздела, постольку значение индукции магнитного поля внутри магнетика и в узкой щели, перпендикулярной направлению магнитного поля, одинакова. Эти особенности в поведении тангенциальной составляющей напряжённости и нормальной составляющей индукции магнит-ного поля лежат в основе методов практических измерений напряжённости и индукции магнитного поля внутри магнетиков.
Электромагнитная индукция
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.184.90 (0.018 с.) |
 На втором этапе дальнейшее увеличение напряжённости внешнего магнитного поля вызывает поворот магнитных мо-ментов доменов в сторону внеш-него магнитного поля.
На втором этапе дальнейшее увеличение напряжённости внешнего магнитного поля вызывает поворот магнитных мо-ментов доменов в сторону внеш-него магнитного поля. Если уменьшать магнитное поле, которое вызвало намаг-ничивание ферромагнетика, то окажется, что зависимость индук-ции магнитного поля в ферромагнетике от напряжённости внешнего магнитного поля не совпадает с начальной кривой намагничивания.
Если уменьшать магнитное поле, которое вызвало намаг-ничивание ферромагнетика, то окажется, что зависимость индук-ции магнитного поля в ферромагнетике от напряжённости внешнего магнитного поля не совпадает с начальной кривой намагничивания. Выделим вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с площадью основания D S. Верхнее основание расположено в среде с магнитной проницаем-остью m1, а нижнее – в среде с m2.
Выделим вблизи границы раздела двух сред цилиндрический объём бесконечно малой высоты с площадью основания D S. Верхнее основание расположено в среде с магнитной проницаем-остью m1, а нижнее – в среде с m2. .
. Перейдём к рассмотрению тангенциальной компоненты векторов В и Н. Воспользуемся для этого теоремой о циркуляции вектора напряжённости магнитного поля (см. разд. 4.2.).
Перейдём к рассмотрению тангенциальной компоненты векторов В и Н. Воспользуемся для этого теоремой о циркуляции вектора напряжённости магнитного поля (см. разд. 4.2.). , т. е. циркуляция вектора напряжённости магнитного поля на границе раздела двух сред равна нулю.
, т. е. циркуляция вектора напряжённости магнитного поля на границе раздела двух сред равна нулю. и
и 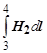 .
.
 .
. .
. На рисунке показано, что в среде с большей магнитной проницаемостью (m1 > m2) силовые линии отклоняются от нор-мали к границе раздела двух сред (это значит, что их густота уве-личивается).
На рисунке показано, что в среде с большей магнитной проницаемостью (m1 > m2) силовые линии отклоняются от нор-мали к границе раздела двух сред (это значит, что их густота уве-личивается).


