

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Объемная плотность энергии упругой волны. Плотность потока энергии. Интенсивность.
Похожие статьи вашей тематики
Вопрос 1
Волны в упругой среде. Основные понятия (источник, виды волн, волновой фронт, волновая поверхность). Уравнение бегущей синусоидальной волны. Характеристики синусоидальной волны. Волновое уравнение. Фазовая скорость волны. Группа волн. Групповая скорость.
А) Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде. Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий. Источниками волн называются тела, которые воздействуют на среду, вызывая колебания её составляющих элементов. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.
Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.
Б)Волновой поверхностью называется геометрическое место точек среды, колеблющихся в фазе.
Волновым фронтом называется геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс. Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Направление распространения колебаний в пространстве происходят вдоль прямых (лучей), которые перпендикулярны волновому фронту.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (от точечного источника в анизотропной среде), цилиндрические (от протяженных источников в виде нити), плоские (от протяженного источника в виде плоскости) и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
В) Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Уравнение плоской бегущей волны, которая распространяется вдоль оси ОУ в положительном направлении, имеет вид:
 , ,
где  – волновое число, А – амплитуда, величина – волновое число, А – амплитуда, величина  – фаза волны, которая в отличие от фазы колебаний зависит не только от времени «t», но и от расстояния колеблющейся точки до источника колебаний «y». Уравнение волны определяет смещение – фаза волны, которая в отличие от фазы колебаний зависит не только от времени «t», но и от расстояния колеблющейся точки до источника колебаний «y». Уравнение волны определяет смещение  любой точки пространства в любой момент времени. любой точки пространства в любой момент времени.
Уравнение плоской отраженной волны: 
Уравнение расходящейся сферической волны имеет вид:
 , где , где  – амплитуда, – амплитуда,  – фаза сферической волны. Физическая величина – фаза сферической волны. Физическая величина  – численно равна амплитуде волны на единичном расстоянии от источника колебаний. – численно равна амплитуде волны на единичном расстоянии от источника колебаний.
Г) Длиной волны  называется расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия. Длина волны – минимальное расстояние, между точками среды, колеблющимися в одинаковой фазе. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны: называется расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия. Длина волны – минимальное расстояние, между точками среды, колеблющимися в одинаковой фазе. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны:  Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания: Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания: 
Д) Уравнения колебаний для любой колебательной системы являются решением соответствующих дифференциальных уравнений. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:  , где , где  – фазовая скорость волны. – фазовая скорость волны.
Скорость и ускорение колеблющейся точки.
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:  , то скорость этой точки по определению есть первая производная от смещения по времени ( , то скорость этой точки по определению есть первая производная от смещения по времени ( ), а ускорение – вторая производная от смещения по t ( ), а ускорение – вторая производная от смещения по t (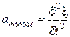 ): ):
 , , 
Волновое уравнение в трехмерном случае имеет вид: 
Е) Групповая скорость
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону.
Скорость перемещения максимума группы волн называется групповой скоростью. Она равна скорости переноса энергии сложной волны.
Связь между групповой и фазовой скоростями имеет вид:
 . .
Чем больше величина  , тем больше групповая скорость отличается от фазовой скорости. Зависимость скорости волны от длины волны называется дисперсией. , тем больше групповая скорость отличается от фазовой скорости. Зависимость скорости волны от длины волны называется дисперсией.
Когда  , групповая скорость меньше фазовой, т.е. длинные волны распространяются быстрее коротких. Это случай нормальной дисперсии волн. , групповая скорость меньше фазовой, т.е. длинные волны распространяются быстрее коротких. Это случай нормальной дисперсии волн.
Когда  , групповая скорость больше фазовой, и дисперсия называется аномальной. , групповая скорость больше фазовой, и дисперсия называется аномальной.
Когда  , дисперсия отсутствует, групповая скорость равна фазовой скорости волны , дисперсия отсутствует, групповая скорость равна фазовой скорости волны  . .
Фазовой скоростью  волны называется скорость распространения данной фазы колебаний.
Скорость распространения волны равна фазовой скорости, если ее частота и длина волны постоянна. Связь длины волны волны называется скорость распространения данной фазы колебаний.
Скорость распространения волны равна фазовой скорости, если ее частота и длина волны постоянна. Связь длины волны  , фазовой скорости , фазовой скорости  и периода колебаний Т, согласно определению длины волны, имеет вид: и периода колебаний Т, согласно определению длины волны, имеет вид:
 . Учитывая соотношение между периодом колебаний точек среды и частотой . Учитывая соотношение между периодом колебаний точек среды и частотой  , получим , получим  .
Для волнового процесса характерна периодичность по времени и по пространству. Время одного колебания Т– период колебаний точек среды. Роль пространственного периода играет длина волны .
Для волнового процесса характерна периодичность по времени и по пространству. Время одного колебания Т– период колебаний точек среды. Роль пространственного периода играет длина волны  . Волновой процесс можно характеризовать не длиной волны, а и волновым числом, которое связано с ней соотношением, . Волновой процесс можно характеризовать не длиной волны, а и волновым числом, которое связано с ней соотношением,  . Отсюда фазовая скорость равна: . Отсюда фазовая скорость равна:  . .
| | | |
Вопрос 2
Вопрос 3
Вопрос 4
Вопрос 5
Существование электромагнитных волн как следствие теории Максвелла. Свойства  электромагнитных волн. Шкала электромагнитных волн. электромагнитных волн. Шкала электромагнитных волн.
А)Электромагнитная природа света.
В основе этой теории лежат уравнения Максвелла:
где rE и rH - векторы напряженности электрического и магнитного полей, rD и rH - векторы электрической и магнитной индукции, rj - вектор тока проводимости, ε и μ - относительные элек-трическая и магнитная проницаемости, ε0 и μ0 - электрическая и магнитная постоянные.
Электромагнитные волны Максвелла были обнаружены Г.Герцем и исследованы на опыте. Колебания возбуждались вибратором, состоящим из двух цинковых шариков, разделенных искровым промежутком. Было показано, что возбуждаемые волны являются поперечными и обнаруживают явления дифракции, поляризации, интерференции.
Что касается отличий, существующих между электромагнитными волнами, обнаруженными Герцем, и световыми, то они могут быть объяснены только отличием длин волн. Можно было утверждать, что явления оптические представляют собой частный случай более общего класса электромагнитных явлений. Видимый свет, непосредственно воспринимаемый человече-ским глазом, занимает узкий интервал длин электромагнитных волн от 0,40 до 0,76 мкм.
Электромагнитными волнами называются возмущения электромагнитного поля, распространяющиеся в пространстве.
Б)
Волновое уравнение
для напряженности электрического поля:  ,
для напряженности магнитного поля ,
для напряженности магнитного поля  ,
где ,
где  – оператор Лапласа.
Канонический вид волнового уравнения (два дифференциальные уравнения): – оператор Лапласа.
Канонический вид волнового уравнения (два дифференциальные уравнения):
 и и 
| Скорость электромагнитной волны
Сравнивая волновые уравнения, получим  . Скорость света в вакууме . Скорость света в вакууме  , а фазовая скорость электромагнитной волны в среде , а фазовая скорость электромагнитной волны в среде  . Видно, что в среде скорость распространения электромагнитных волн меньше, чем в вакууме ( . Видно, что в среде скорость распространения электромагнитных волн меньше, чем в вакууме ( ).
Величина ).
Величина  – показатель преломления среды, зависит от электрических и магнитных свойств среды. – показатель преломления среды, зависит от электрических и магнитных свойств среды.
| Уравнение электромагнитной волны
Решением волновых уравнений являются уравнение электромагнитной волны. Для волны, распространяющейся по направлению радиус– вектора  , уравнения электромагнитной волны имеют вид , уравнения электромагнитной волны имеют вид  , где волновой вектор , где волновой вектор  ; ;  – единичный вектор вдоль радиус– вектора – единичный вектор вдоль радиус– вектора  , модуль волнового вектора равен , модуль волнового вектора равен  . .
| Электромагнитная волна – поперечная волна
Вектора напряженностей электрического и магнитного полей перпендикулярны и между собой, и направлению распространения волны или скорости волны. Вектора  , ,  , ,  составляют правую тройку векторов (рисунок 5.6.1).
Направления этих векторов связаны правилом буравчика: рукоять буравчика вращается от составляют правую тройку векторов (рисунок 5.6.1).
Направления этих векторов связаны правилом буравчика: рукоять буравчика вращается от  к к  по кратчайшему расстоянию, буравчик движется вдоль направления по кратчайшему расстоянию, буравчик движется вдоль направления  . Отметим, что взаимное расположение осей правой декартовой система координат такое же, как у векторов . Отметим, что взаимное расположение осей правой декартовой система координат такое же, как у векторов  , ,  , ,  , электромагнитной волны. Для сравнения ориентации тройки векторов , электромагнитной волны. Для сравнения ориентации тройки векторов  , ,  , ,  приведено на рисунке 5.6.1. расположение осей X, Y, Z правой декартовой системы координат. приведено на рисунке 5.6.1. расположение осей X, Y, Z правой декартовой системы координат.
 Рисунок 5.6.1.– Правая тройка векторов а) для электромагнитной волны, б) декартова система координат
Рисунок 5.6.1.– Правая тройка векторов а) для электромагнитной волны, б) декартова система координат
| Соотношение между величинами напряженностей электрического и магнитного полей волны.
Для любого момента времени верно соотношение  , это означает, что взаимно перпендикулярные векторы , это означает, что взаимно перпендикулярные векторы  и и  колеблются в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений. Соотношение справедливо также и для сферической волны, т.е. для любой бегущей электромагнитной волны независимо от формы ее волновой поверхности. колеблются в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений. Соотношение справедливо также и для сферической волны, т.е. для любой бегущей электромагнитной волны независимо от формы ее волновой поверхности.
| Монохроматическая волна не ограничена в пространстве и во времени. Для электрической составляющей монохроматической волны верны соотношения  , где , где  – разность фаз колебаний – разность фаз колебаний  и и  , ,  и и  их амплитуды. Магнитную составляющую найдем из соотношений их амплитуды. Магнитную составляющую найдем из соотношений  , ,  . В зависимости от разности фаз . В зависимости от разности фаз  в уравнении монохроматическая волна может быть различной поляризации.
При в уравнении монохроматическая волна может быть различной поляризации.
При  (m=0, 1, 2….) волна будет линейно поляризованной или плоско поляризованной волной. На рисунке 5.6.2. показаны значения векторов (m=0, 1, 2….) волна будет линейно поляризованной или плоско поляризованной волной. На рисунке 5.6.2. показаны значения векторов  и и  поля плоской линейно поляризованной монохроматической волны в различных точках пространства, взятые в один и тот же момент времени. Оси ОZ и ОX проведены в направлениях соответствующих колебаний векторов поля плоской линейно поляризованной монохроматической волны в различных точках пространства, взятые в один и тот же момент времени. Оси ОZ и ОX проведены в направлениях соответствующих колебаний векторов  и и  .
Уравнение плоской линейно поляризованной волны имеет вид: .
Уравнение плоской линейно поляризованной волны имеет вид:

 Рисунок 5.6.2 – Значения векторов
Рисунок 5.6.2 – Значения векторов  и и  поля плоской линейно поляризованной
монохроматической волны в различных точках пространства, взятые в один и тот же момент времени
Плоскость, в которой происходит колебание вектора поля плоской линейно поляризованной
монохроматической волны в различных точках пространства, взятые в один и тот же момент времени
Плоскость, в которой происходит колебание вектора  называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора  – плоскостью колебаний. – плоскостью колебаний.
| | | В) Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения (в вакууме) постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
| Название диапазона
| Длины волн, λ
| Частоты, ν
| Источники
| | Радиоволны
| Сверхдлинные
| более 10 км
| менее 30 кГц
| Атмосферные имагнитосферныеявления. Радиосвязь.
| | Длинные
| 10 км — 1 км
| 30 кГц — 300 кГц
| | Средние
| 1 км — 100 м
| 300 кГц — 3 МГц
| | Короткие
| 100 м — 10 м
| 3 МГц — 30 МГц
| | Ультракороткие
| 10 м — 1 мм
| 30 МГц — 300 ГГц
| | Инфракрасное излучение
| 1 мм — 780 нм
| 300 ГГц — 429 ТГц
| Излучение молекул и атомов при тепловых и электрических воздействиях.
| | Видимое (оптическое) излучение
| 780—380 нм
| 429 ТГц — 750 ТГц
| | Ультрафиолетовое
| 380 — 10 нм
| 7,5·1014 Гц — 3·1016 Гц
| Излучение атомов под воздействием ускоренных электронов.
| | Рентгеновские
| 10 нм — 5 пм
| 3·1016 — 6·1019 Гц
| Атомные процессы при воздействии ускоренных заряженных частиц.
| | Гамма
| менее 5 пм
| более 6·1019 Гц
| Ядерные и космические процессы, радиоактивный распад.
|
Вопрос 6
Вопрос 7
Вопрос 8
Волновые свойства света. Когерентность. Способы получения когерентных волн. Интерференция света от двух источников (опыт Юнга). Координаты минимумов и максимумов. Ширина интерференционной полосы.
А) Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.
Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты).
Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны. В продольной волне поляризация возникнуть не может, так как направление колебаний в этом типе волн всегда совпадают с направлением распространения. Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.
Б)Два колебательных процесса называются когерентными, если разность фаз складывающихся колебаний остается постоянной в течение времени, достаточного для наблюдений.
В) Способы получения когерентных волн.
Получение когерентных волн для реализации интерференции в оптике осуществляется двумя способами:
инструментальное получение из данного источника двух когерентных;
деление фронта волны.
Схемы получения когерентных волн в первом случае основаны на получении двух источников, которые являются двумя изображениями данного единого излучающего центра (метод Юнга, бипризма Френеля, зеркала Френеля). Во втором случае получение когерентных волн происходит делением волны в пределах цуга на две волны (интерферометр Майкельсона, тонкие пленки, клин, кольца Ньютона).
6.3.1. Условия осуществления явления интерференции
Когерентные волны.
Интерференция (см. главу 5). Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям, и источники, создающие такие волны, называются когерентными. Условию когерентности удовлетворяют монохроматические волны, имеющие одинаковые частоты и постоянные разности начальных фаз. Монохроматическая волна характеризуется определенной длиной волны  и связанной с ней частотой и связанной с ней частотой  , где , где  – скорость света в вакууме. – скорость света в вакууме.
| | Способы получения когерентных волн.
Получение когерентных волн для реализации интерференции в оптике осуществляется двумя способами:
инструментальное получение из данного источника двух когерентных;
деление фронта волны.
Схемы получения когерентных волн в первом случае основаны на получении двух источников, которые являются двумя изображениями данного единого излучающего центра (метод Юнга, бипризма Френеля, зеркала Френеля). Во втором случае получение когерентных волн происходит делением волны в пределах цуга на две волны (интерферометр Майкельсона, тонкие пленки, клин, кольца Ньютона).
| Оптическая длина пути.
Произведение расстояния, пройденного световой волной, на показатель преломления среды называетсяоптической длиной пути или оптическим ходом волны (луча)  , где , где  – геометрический путь, т.е. расстояние, пройденное волной, – геометрический путь, т.е. расстояние, пройденное волной,  – показатель преломления среды. Для расчета интерференции пользуются оптической разностью хода интерферирующих волн, тогда условия максимумов и минимумов формулируются для соответствующих значений длин волн в вакууме. Если пользоваться понятием геометрической разности хода при прохождении света через разные среды, то условия интерференции усложняется, надо будет учитывать изменение длины волны в этих средах. – показатель преломления среды. Для расчета интерференции пользуются оптической разностью хода интерферирующих волн, тогда условия максимумов и минимумов формулируются для соответствующих значений длин волн в вакууме. Если пользоваться понятием геометрической разности хода при прохождении света через разные среды, то условия интерференции усложняется, надо будет учитывать изменение длины волны в этих средах.
| Отражение волн от поверхности. При расчете оптического пути и оптической разности хода надо помнить: при отражении волны от оптически более плотной среды, происходит изменение ее фазы на величину π, что соответствует прибавлению в ход волны или вычитанию из хода волны величины  . .
| Условия максимума интенсивности:
для разности фаз  ,
для оптической разности хода ,
для оптической разности хода  , где , где  – длина волны в вакууме, а – длина волны в вакууме, а  Условия минимума интенсивности
для разности фаз
Условия минимума интенсивности
для разности фаз  для оптической разности хода
для оптической разности хода  . Во всех случаев . Во всех случаев 
|
Вопрос 9
Вопрос 10
Вопрос 11
Вопрос 12
Вопрос 13
Вопрос 14
Вопрос 15
Вопрос 16
Вопрос 17
Вопрос 18
Искусственная оптическая анизотропия (фотоупругость, эффект Керра, эффект Коттона -Мутона).
Оптическая анизотропия. Двойное лучепреломление В том случае, если скорость света в каждой точке среды не зависит ни от направления распространения волны, ни от характера поляризации, среда будет оптически изотропной. Оптическая анизотропия кристалла может быть обусловлена как электрической анизотропией образующих его частиц, так и анизотропией поля сил взаимодействия между ними. Характер этого поля, т.е. его изотропность или анизотропность, зависит от степени симметрии решетки кристалла. Только кристаллы кубической системы (например, каменная соль NaCl), обладающие весьма высокой степенью симметрии решетки, являются оптически изотропными. Все остальные кристаллы, независимо от электрических свойств образующих их частиц, оптически анизотропны. При распространении света в анизотропных средах наблюдается явление, получившее название двойного лучепреломления. Это явление заключается в том, что упавший на кристалл луч разделяется внутри кристалла на два луча (обыкновенный и необыкновенный), которые распространяются с разными скоростями и в различных направлениях. Двойное лучепреломление возникает в том случае, если неполяризованный свет падает под некоторым углом к оптической оси кристалла (рисунок 6.5.3). Оптическая ось кристалла задает направление, вдоль которого не происходит двойное лучепреломление в анизотропном кристалле.
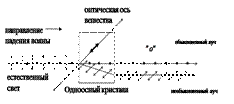 Рисунок 6.5.3. – Двойное лучепреломление. Сечение плоскостью падения луча.
Обыкновенным лучом называется луч (о), подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он в кристалле пройдет, не отклоняясь;
Необыкновенным лучом называется луч (е), не подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он преломляется в кристалле, отклоняясь на некоторый угол (рисунок 6.5.3).
Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных направлениях. Колебания вектора Рисунок 6.5.3. – Двойное лучепреломление. Сечение плоскостью падения луча.
Обыкновенным лучом называется луч (о), подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он в кристалле пройдет, не отклоняясь;
Необыкновенным лучом называется луч (е), не подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он преломляется в кристалле, отклоняясь на некоторый угол (рисунок 6.5.3).
Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных направлениях. Колебания вектора 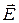 в обыкновенном луче перпендикулярны плоскости падения луча и оптической оси, они изображены точками на рисунке 6.5.3. Колебания вектора в обыкновенном луче перпендикулярны плоскости падения луча и оптической оси, они изображены точками на рисунке 6.5.3. Колебания вектора 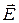 необыкновенного луча параллельны оптической оси (стрелки на рисунке 6.5.3). Показатели преломления обыкновенного и необыкновенного лучей различны, поэтому и скорости распространения света соответственно не равны: необыкновенного луча параллельны оптической оси (стрелки на рисунке 6.5.3). Показатели преломления обыкновенного и необыкновенного лучей различны, поэтому и скорости распространения света соответственно не равны: 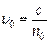 и и  . При прохождении обоими лучами одного и того же расстояния d в кристалле между ними возникает оптическая разность хода и возникает разность фаз: . При прохождении обоими лучами одного и того же расстояния d в кристалле между ними возникает оптическая разность хода и возникает разность фаз: 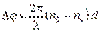 , где , где 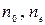 – показатели преломления обыкновенного и необыкновенного лучей, – показатели преломления обыкновенного и необыкновенного лучей, 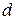 – толщина кристалла. – толщина кристалла.
| | Искусственная анизотропия
| Фотоупругость – явление, когда под влиянием механической деформации среда, бывшая оптически изотропной становится оптически анизотропной и при прохождении света наблюдается двойное лучепреломление. Разность показателей преломления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси, пропорциональна нормальному напряжению 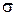 : : 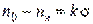 , где , где 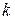 – коэффициент, зависящий от свойств вещества. При прохождении обыкновенным и необыкновенным лучами одного и того же расстояния, толщины пластинки d, между ними возникает оптическая разность хода – коэффициент, зависящий от свойств вещества. При прохождении обыкновенным и необыкновенным лучами одного и того же расстояния, толщины пластинки d, между ними возникает оптическая разность хода 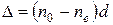 , а значит и разность фаз: , а значит и разность фаз: 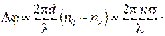
| Эффект Керра. Возникновение двойного лучепреломления в изотропных жидкостях и в изотропных аморфных твердых телах под воздействием электрического поля называется эффектом Керра. Для этого кювету с жидкостью помещают в электрическое поле конденсатора. Разность показателей преломления поляризованной жидкости для необыкновенного и обыкновенного лучей монохроматического света в направлении, перпендикулярном вектору напряженности внешнего электрического поля 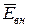 , пропорциональна квадрату амплитуды внешнего поля Е2вн: , пропорциональна квадрату амплитуды внешнего поля Е2вн:  , где λ – длина волны света в вакууме, В – константа Керра. Между необыкновенным и обыкновенным лучами при прохождении расстояния, равное длине кюветы возникает сдвиг фаз: , где λ – длина волны света в вакууме, В – константа Керра. Между необыкновенным и обыкновенным лучами при прохождении расстояния, равное длине кюветы возникает сдвиг фаз:  , где d – длина ячейки с изотропной жидкостью, равная длине пластин конденсатора, в который помещена ячейка, U = Евн·а – напряжение, подаваемое на конденсатор, а – расстояние между пластинами конденсатора. , где d – длина ячейки с изотропной жидкостью, равная длине пластин конденсатора, в который помещена ячейка, U = Евн·а – напряжение, подаваемое на конденсатор, а – расстояние между пластинами конденсатора.
| Эффект Коттона – Мутона. Явление возникновения оптической анизотропии у изотропного вещества под влиянием сильного внешнего магнитного поля получило название эффекта Коттона – Мутона. Разность показателей преломления вещества для необыкновенного и обыкновенного лучей, распространяющихся перпендикулярно направлению оптической оси (направление главной оптической оси задается направлением вектора магнитной индукции  внешнего однородного магнитного поля) определяется соотношением: внешнего однородного магнитного поля) определяется соотношением: 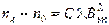 , где С – постоянная Коттона – Мутона, зависящая от природы вещества, длина волны света падающего света λ и температуры. Между необыкновенным и обыкновенным лучами возникает сдвиг по фазе: , где С – постоянная Коттона – Мутона, зависящая от природы вещества, длина волны света падающего света λ и температуры. Между необыкновенным и обыкновенным лучами возникает сдвиг по фазе:  , где d – длина образца исследуемого вещества. , где d – длина образца исследуемого вещества.
|
Вопрос 19
Вопрос 20
Вопрос 21
Вопрос 22
Основы голографии.
Голография основывается на двух физических явлениях - дифракции и интереференции световых волн.
Физическая идея состоит в том, что при наложении двух световых пучков, при определенных условиях возникает интерференционная картина, то есть, в пространстве возникают максимумы и минимумы интенсивности света (это подобно тому, как две системы волн на воде при пересечении образуют чередующиеся максимумы и минимумы амплитуды волн). Для того, чтобы эта интерференционная картина была устойчивой в течение времени, необходимого для наблюдения, и ее можно было записать, эти две световых волны должны быть согласованы в пространстве и во времени. Такие согласованные волны называются когерентными.
Если волны встречаются в фазе, то они складываются друг с другом и дают результирующую волну с амплитудой, равной сумме их амплитуд. Если же они встречаются в противофазе, то будут гасить одна другую. Между двумя этими крайними положениями наблюдаются различные ситуации сложения волн. Результирующая сложения двух когерентных волн будет всегда стоячей волной. То есть интерференционная картина будет устойчива во времени. Это явление лежит в основе получения и восстановления голограмм.
Обычные источники света не обладают достаточной степенью когерентности для использования в голографии. Поэтому решающее значение для ее развития имело изобретение в 1960 г. оптического квантового генератора или лазера - удивительного источника излучения, обладающего необходимой степенью когерентности и могущего излучать строго одну длину волны.
Вопрос 23
Вопрос 24
Экспериментальные законы теплового излучения: Стефана – Больцмана, закон смещения Вина, 2-й закон Вина. Распределение энергии в спектре АЧТ. Гипотеза Планка о квантовом характере излучения. Функция Планка.
Экспериментальные законы теплового излучения 1.Закон Стефана-Больцмана для абсолютно черного тела  , где , где  – константа Стефана-Больцмана. Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 2. Серым телом называется тело, поглощательная способность которого меньше единицы и не зависит от длины волны падающего излучения, направления его распространения и поляризации – константа Стефана-Больцмана. Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 2. Серым телом называется тело, поглощательная способность которого меньше единицы и не зависит от длины волны падающего излучения, направления его распространения и поляризации  , ,  – коэффициент черноты (степень нечерноты, степень серости тела). Закон Стефана-Больцмана для серых тел имеет вид: – коэффициент черноты (степень нечерноты, степень серости тела). Закон Стефана-Больцмана для серых тел имеет вид:  . 3. Закон смещения Вина: . 3. Закон смещения Вина:  , где величина , где величина  первая константа Вина. Длина волны первая константа Вина. Длина волны  , на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. 4.Второй закон Вина: , на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. 4.Второй закон Вина:  . Величина . Величина  называется вторая константа Вина. Максимальное значение излучательной способности абсолютно черного тела прямо пропорционально пятой степени его абсолютной температуры. называется вторая константа Вина. Максимальное значение излучательной способности абсолютно черного тела прямо пропорционально пятой степени его абсолютной температуры.
| Теоретический вид функции Кирхгофа удалось установить немецкому физику Планку путем введения квантовой гипотезы.
Квантовая гипотеза Планка. В качестве теоретической модели абсолютно черного тела можно взять бесконечную систему гармонических осцилляторов со всевозможными собственными частотами, которые соответствуют монохроматическим компонентам излучения. По законам классической физики осциллятор может иметь любую энергию, и меняться энергия системы может непрерывно. Планк предположил, что гармонический осциллятор частоты  может обладать только рядом дискретных значений энергии, которые отличаются друг от друга на целое число элементарных порций величиной может обладать только рядом дискретных значений энергии, которые отличаются друг от друга на целое число элементарных порций величиной  . Квант энергии . Квант энергии  , где , где  , где , где  – частота излучения, постоянная – частота излучения, постоянная 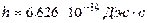 называется постоянная Планка (квант действия). Редуцированная постоянная Планка называется постоянная Планка (квант действия). Редуцированная постоянная Планка  Дж× с. Учитывая новые квантовые законы, Планк получил для функции Кирхгофа следующее выражение: Дж× с. Учитывая новые квантовые законы, Планк получил для функции Кирхгофа следующее выражение:  . Формула Планка для излучательной способности . Формула Планка для излучательной способности  абсолютно черного имеет вид: абсолютно черного имеет вид:  . Вид графика . Вид графика  совпадает с кривыми, которые представлены на рисунке 6.7.1. совпадает с кривыми, которые представлены на рисунке 6.7.1.
|
Вопрос 25
Внешний фотоэффект. Основные законы внешнего фотоэффекта. Невозможность объяснить законы внешнего фотоэффекта с точки зрения волновой теории света. Уравнение Эйнштейна для внешнего фотоэффекта. ВАХ внешнего фотоэффекта.
А)Внешним фотоэффектом (фотоэлектронной эмиссией) называется явление испускания электронов веществом под действием света с поверхности вещества. Электроны, вылетающие с вещества, называютсяфотоэлектронами. При упорядоченном движении фотоэлектронов во внешнем электрическом поле возникаетфототок. При внутреннем фотоэффекте электроны, оставаясь в теле, изменяют под действием света свои энергетические состояния, что приводит к изменению некоторых свойств вещества, например, его электропроводности. На рисунке 6.7.2 представлена схема для изучения законов внешнего фотоэффекта. Катод К вакуумного фотодиода освещается светом через окно О. Д)Зависимость фототока  от разности потенциалов от разности потенциалов  между анодом А и катодом К называется вольтамперной характеристикой (ВАХ) вакуумного фотодиода, она представлен на рисунке 6.7.3. между анодом А и катодом К называется вольтамперной характеристикой (ВАХ) вакуумного фотодиода, она представлен на рисунке 6.7.3.
 Рисунок 6.7.2. – Схема изучения ВАХ фотодиода
Рисунок 6.7.2. – Схема изучения ВАХ фотодиода
 Рисунок 6.7.3. – Вольт – амперная характеристика (ВАХ) фотодиода.
Предельное значение фототока
Рисунок 6.7.3. – Вольт – амперная характеристика (ВАХ) фотодиода.
Предельное значение фототока  называется током насыщения и означает, что все вылетевшие в единицу времени с катода под влиянием света электроны достигли анода. Существование фототока при отрицательных значениях называется током насыщения и означает, что все вылетевшие в единицу времени с катода под влиянием света электроны достигли анода. Существование фототока при отрицательных значениях  (т.е. когда катод К подключен к плюсу, анод А – к минусу источника тока) свидетельствует о том, что фотоэлектроны из катода выходят с некоторой начальной скоростью. Максимальная начальная скорость фотоэлектронов (т.е. когда катод К подключен к плюсу, анод А – к минусу источника тока) свидетельствует о том, что фотоэлектроны из катода выходят с некоторой начальной скоростью. Максимальная начальная скорость фотоэлектронов  связана с характеристикой задерживающего электрического поля – задерживающим напряжением связана с характеристикой задерживающего электрического поля – задерживающим напряжением 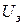 соотношением: соотношением:  , где , где  |
| Поделиться:
|
|



 ,
, – волновое число, А – амплитуда, величина
– волновое число, А – амплитуда, величина  – фаза волны, которая в отличие от фазы колебаний зависит не только от времени «t», но и от расстояния колеблющейся точки до источника колебаний «y». Уравнение волны определяет смещение
– фаза волны, которая в отличие от фазы колебаний зависит не только от времени «t», но и от расстояния колеблющейся точки до источника колебаний «y». Уравнение волны определяет смещение  любой точки пространства в любой момент времени.
любой точки пространства в любой момент времени.
 , где
, где  – амплитуда,
– амплитуда,  – фаза сферической волны. Физическая величина
– фаза сферической волны. Физическая величина  – численно равна амплитуде волны на единичном расстоянии от источника колебаний.
– численно равна амплитуде волны на единичном расстоянии от источника колебаний. называется расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия. Длина волны – минимальное расстояние, между точками среды, колеблющимися в одинаковой фазе. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны:
называется расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия. Длина волны – минимальное расстояние, между точками среды, колеблющимися в одинаковой фазе. Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны:  Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:
Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания: 
 , где
, где  – фазовая скорость волны.
– фазовая скорость волны. , то скорость этой точки по определению есть первая производная от смещения по времени (
, то скорость этой точки по определению есть первая производная от смещения по времени ( ), а ускорение – вторая производная от смещения по t (
), а ускорение – вторая производная от смещения по t (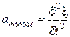 ):
): ,
, 

 .
. , тем больше групповая скорость отличается от фазовой скорости. Зависимость скорости волны от длины волны называется дисперсией.
, тем больше групповая скорость отличается от фазовой скорости. Зависимость скорости волны от длины волны называется дисперсией. , групповая скорость меньше фазовой, т.е. длинные волны распространяются быстрее коротких. Это случай нормальной дисперсии волн.
, групповая скорость меньше фазовой, т.е. длинные волны распространяются быстрее коротких. Это случай нормальной дисперсии волн. , групповая скорость больше фазовой, и дисперсия называется аномальной.
, групповая скорость больше фазовой, и дисперсия называется аномальной. , дисперсия отсутствует, групповая скорость равна фазовой скорости волны
, дисперсия отсутствует, групповая скорость равна фазовой скорости волны  .
. волны называется скорость распространения данной фазы колебаний.
Скорость распространения волны равна фазовой скорости, если ее частота и длина волны постоянна. Связь длины волны
волны называется скорость распространения данной фазы колебаний.
Скорость распространения волны равна фазовой скорости, если ее частота и длина волны постоянна. Связь длины волны  и периода колебаний Т, согласно определению длины волны, имеет вид:
и периода колебаний Т, согласно определению длины волны, имеет вид:
 . Учитывая соотношение между периодом колебаний точек среды и частотой
. Учитывая соотношение между периодом колебаний точек среды и частотой  , получим
, получим  .
Для волнового процесса характерна периодичность по времени и по пространству. Время одного колебания Т– период колебаний точек среды. Роль пространственного периода играет длина волны
.
Для волнового процесса характерна периодичность по времени и по пространству. Время одного колебания Т– период колебаний точек среды. Роль пространственного периода играет длина волны  . Волновой процесс можно характеризовать не длиной волны, а и волновым числом, которое связано с ней соотношением,
. Волновой процесс можно характеризовать не длиной волны, а и волновым числом, которое связано с ней соотношением,  . Отсюда фазовая скорость равна:
. Отсюда фазовая скорость равна:  .
.
 электромагнитных волн. Шкала электромагнитных волн.
электромагнитных волн. Шкала электромагнитных волн. ,
для напряженности магнитного поля
,
для напряженности магнитного поля  ,
где
,
где  – оператор Лапласа.
Канонический вид волнового уравнения (два дифференциальные уравнения):
– оператор Лапласа.
Канонический вид волнового уравнения (два дифференциальные уравнения):
 и
и 
 . Скорость света в вакууме
. Скорость света в вакууме  , а фазовая скорость электромагнитной волны в среде
, а фазовая скорость электромагнитной волны в среде  . Видно, что в среде скорость распространения электромагнитных волн меньше, чем в вакууме (
. Видно, что в среде скорость распространения электромагнитных волн меньше, чем в вакууме ( ).
Величина
).
Величина  – показатель преломления среды, зависит от электрических и магнитных свойств среды.
– показатель преломления среды, зависит от электрических и магнитных свойств среды.
 , уравнения электромагнитной волны имеют вид
, уравнения электромагнитной волны имеют вид  , где волновой вектор
, где волновой вектор  ;
;  – единичный вектор вдоль радиус– вектора
– единичный вектор вдоль радиус– вектора  .
.
 ,
,  ,
,  составляют правую тройку векторов (рисунок 5.6.1).
Направления этих векторов связаны правилом буравчика: рукоять буравчика вращается от
составляют правую тройку векторов (рисунок 5.6.1).
Направления этих векторов связаны правилом буравчика: рукоять буравчика вращается от  к
к  по кратчайшему расстоянию, буравчик движется вдоль направления
по кратчайшему расстоянию, буравчик движется вдоль направления  . Отметим, что взаимное расположение осей правой декартовой система координат такое же, как у векторов
. Отметим, что взаимное расположение осей правой декартовой система координат такое же, как у векторов  ,
,  , электромагнитной волны. Для сравнения ориентации тройки векторов
, электромагнитной волны. Для сравнения ориентации тройки векторов  ,
,  приведено на рисунке 5.6.1. расположение осей X, Y, Z правой декартовой системы координат.
приведено на рисунке 5.6.1. расположение осей X, Y, Z правой декартовой системы координат.
 Рисунок 5.6.1.– Правая тройка векторов а) для электромагнитной волны, б) декартова система координат
Рисунок 5.6.1.– Правая тройка векторов а) для электромагнитной волны, б) декартова система координат
 , это означает, что взаимно перпендикулярные векторы
, это означает, что взаимно перпендикулярные векторы  колеблются в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений. Соотношение справедливо также и для сферической волны, т.е. для любой бегущей электромагнитной волны независимо от формы ее волновой поверхности.
колеблются в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений. Соотношение справедливо также и для сферической волны, т.е. для любой бегущей электромагнитной волны независимо от формы ее волновой поверхности.
 , где
, где  – разность фаз колебаний
– разность фаз колебаний  и
и  ,
,  и
и  их амплитуды. Магнитную составляющую найдем из соотношений
их амплитуды. Магнитную составляющую найдем из соотношений  ,
,  . В зависимости от разности фаз
. В зависимости от разности фаз  (m=0, 1, 2….) волна будет линейно поляризованной или плоско поляризованной волной. На рисунке 5.6.2. показаны значения векторов
(m=0, 1, 2….) волна будет линейно поляризованной или плоско поляризованной волной. На рисунке 5.6.2. показаны значения векторов  и
и  поля плоской линейно поляризованной монохроматической волны в различных точках пространства, взятые в один и тот же момент времени. Оси ОZ и ОX проведены в направлениях соответствующих колебаний векторов
поля плоской линейно поляризованной монохроматической волны в различных точках пространства, взятые в один и тот же момент времени. Оси ОZ и ОX проведены в направлениях соответствующих колебаний векторов  .
Уравнение плоской линейно поляризованной волны имеет вид:
.
Уравнение плоской линейно поляризованной волны имеет вид:

 Рисунок 5.6.2 – Значения векторов
Рисунок 5.6.2 – Значения векторов  поля плоской линейно поляризованной
монохроматической волны в различных точках пространства, взятые в один и тот же момент времени
Плоскость, в которой происходит колебание вектора
поля плоской линейно поляризованной
монохроматической волны в различных точках пространства, взятые в один и тот же момент времени
Плоскость, в которой происходит колебание вектора  – плоскостью колебаний.
– плоскостью колебаний.
 , где
, где  – скорость света в вакууме.
– скорость света в вакууме.
 , где
, где  – геометрический путь, т.е. расстояние, пройденное волной,
– геометрический путь, т.е. расстояние, пройденное волной,  – показатель преломления среды. Для расчета интерференции пользуются оптической разностью хода интерферирующих волн, тогда условия максимумов и минимумов формулируются для соответствующих значений длин волн в вакууме. Если пользоваться понятием геометрической разности хода при прохождении света через разные среды, то условия интерференции усложняется, надо будет учитывать изменение длины волны в этих средах.
– показатель преломления среды. Для расчета интерференции пользуются оптической разностью хода интерферирующих волн, тогда условия максимумов и минимумов формулируются для соответствующих значений длин волн в вакууме. Если пользоваться понятием геометрической разности хода при прохождении света через разные среды, то условия интерференции усложняется, надо будет учитывать изменение длины волны в этих средах.
 .
.
 ,
для оптической разности хода
,
для оптической разности хода  , где
, где  – длина волны в вакууме, а
– длина волны в вакууме, а  Условия минимума интенсивности
для разности фаз
Условия минимума интенсивности
для разности фаз  для оптической разности хода
для оптической разности хода  . Во всех случаев
. Во всех случаев 
 Рисунок 6.5.3. – Двойное лучепреломление. Сечение плоскостью падения луча.
Обыкновенным лучом называется луч (о), подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он в кристалле пройдет, не отклоняясь;
Необыкновенным лучом называется луч (е), не подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он преломляется в кристалле, отклоняясь на некоторый угол (рисунок 6.5.3).
Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных направлениях. Колебания вектора
Рисунок 6.5.3. – Двойное лучепреломление. Сечение плоскостью падения луча.
Обыкновенным лучом называется луч (о), подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он в кристалле пройдет, не отклоняясь;
Необыкновенным лучом называется луч (е), не подчиняющийся закону преломления света, поэтому при нормальном падении света на кристалл он преломляется в кристалле, отклоняясь на некоторый угол (рисунок 6.5.3).
Обыкновенный и необыкновенный лучи поляризованы во взаимно перпендикулярных направлениях. Колебания вектора 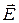 в обыкновенном луче перпендикулярны плоскости падения луча и оптической оси, они изображены точками на рисунке 6.5.3. Колебания вектора
в обыкновенном луче перпендикулярны плоскости падения луча и оптической оси, они изображены точками на рисунке 6.5.3. Колебания вектора 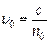 и
и  . При прохождении обоими лучами одного и того же расстояния d в кристалле между ними возникает оптическая разность хода и возникает разность фаз:
. При прохождении обоими лучами одного и того же расстояния d в кристалле между ними возникает оптическая разность хода и возникает разность фаз: 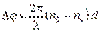 , где
, где 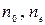 – показатели преломления обыкновенного и необыкновенного лучей,
– показатели преломления обыкновенного и необыкновенного лучей, 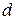 – толщина кристалла.
– толщина кристалла.
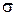 :
: 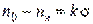 , где
, где 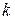 – коэффициент, зависящий от свойств вещества. При прохождении обыкновенным и необыкновенным лучами одного и того же расстояния, толщины пластинки d, между ними возникает оптическая разность хода
– коэффициент, зависящий от свойств вещества. При прохождении обыкновенным и необыкновенным лучами одного и того же расстояния, толщины пластинки d, между ними возникает оптическая разность хода 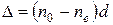 , а значит и разность фаз:
, а значит и разность фаз: 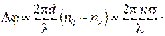
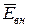 , пропорциональна квадрату амплитуды внешнего поля Е2вн:
, пропорциональна квадрату амплитуды внешнего поля Е2вн:  , где λ – длина волны света в вакууме, В – константа Керра. Между необыкновенным и обыкновенным лучами при прохождении расстояния, равное длине кюветы возникает сдвиг фаз:
, где λ – длина волны света в вакууме, В – константа Керра. Между необыкновенным и обыкновенным лучами при прохождении расстояния, равное длине кюветы возникает сдвиг фаз:  , где d – длина ячейки с изотропной жидкостью, равная длине пластин конденсатора, в который помещена ячейка, U = Евн·а – напряжение, подаваемое на конденсатор, а – расстояние между пластинами конденсатора.
, где d – длина ячейки с изотропной жидкостью, равная длине пластин конденсатора, в который помещена ячейка, U = Евн·а – напряжение, подаваемое на конденсатор, а – расстояние между пластинами конденсатора.
 внешнего однородного магнитного поля) определяется соотношением:
внешнего однородного магнитного поля) определяется соотношением: 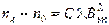 , где С – постоянная Коттона – Мутона, зависящая от природы вещества, длина волны света падающего света λ и температуры. Между необыкновенным и обыкновенным лучами возникает сдвиг по фазе:
, где С – постоянная Коттона – Мутона, зависящая от природы вещества, длина волны света падающего света λ и температуры. Между необыкновенным и обыкновенным лучами возникает сдвиг по фазе:  , где d – длина образца исследуемого вещества.
, где d – длина образца исследуемого вещества.
 , где
, где  – константа Стефана-Больцмана. Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 2. Серым телом называется тело, поглощательная способность которого меньше единицы и не зависит от длины волны падающего излучения, направления его распространения и поляризации
– константа Стефана-Больцмана. Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры. 2. Серым телом называется тело, поглощательная способность которого меньше единицы и не зависит от длины волны падающего излучения, направления его распространения и поляризации  ,
,  – коэффициент черноты (степень нечерноты, степень серости тела). Закон Стефана-Больцмана для серых тел имеет вид:
– коэффициент черноты (степень нечерноты, степень серости тела). Закон Стефана-Больцмана для серых тел имеет вид:  . 3. Закон смещения Вина:
. 3. Закон смещения Вина:  , где величина
, где величина  первая константа Вина. Длина волны
первая константа Вина. Длина волны  , на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. 4.Второй закон Вина:
, на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. 4.Второй закон Вина:  . Величина
. Величина  называется вторая константа Вина. Максимальное значение излучательной способности абсолютно черного тела прямо пропорционально пятой степени его абсолютной температуры.
называется вторая константа Вина. Максимальное значение излучательной способности абсолютно черного тела прямо пропорционально пятой степени его абсолютной температуры.
 может обладать только рядом дискретных значений энергии, которые отличаются друг от друга на целое число элементарных порций величиной
может обладать только рядом дискретных значений энергии, которые отличаются друг от друга на целое число элементарных порций величиной  . Квант энергии
. Квант энергии  , где
, где  , где
, где 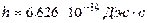 называется постоянная Планка (квант действия). Редуцированная постоянная Планка
называется постоянная Планка (квант действия). Редуцированная постоянная Планка  Дж× с. Учитывая новые квантовые законы, Планк получил для функции Кирхгофа следующее выражение:
Дж× с. Учитывая новые квантовые законы, Планк получил для функции Кирхгофа следующее выражение:  . Формула Планка для излучательной способности
. Формула Планка для излучательной способности  абсолютно черного имеет вид:
абсолютно черного имеет вид:  . Вид графика
. Вид графика  совпадает с кривыми, которые представлены на рисунке 6.7.1.
совпадает с кривыми, которые представлены на рисунке 6.7.1.
 от разности потенциалов
от разности потенциалов  между анодом А и катодом К называется вольтамперной характеристикой (ВАХ) вакуумного фотодиода, она представлен на рисунке 6.7.3.
между анодом А и катодом К называется вольтамперной характеристикой (ВАХ) вакуумного фотодиода, она представлен на рисунке 6.7.3.
 Рисунок 6.7.2. – Схема изучения ВАХ фотодиода
Рисунок 6.7.2. – Схема изучения ВАХ фотодиода
 Рисунок 6.7.3. – Вольт – амперная характеристика (ВАХ) фотодиода.
Предельное значение фототока
Рисунок 6.7.3. – Вольт – амперная характеристика (ВАХ) фотодиода.
Предельное значение фототока  называется током насыщения и означает, что все вылетевшие в единицу времени с катода под влиянием света электроны достигли анода. Существование фототока при отрицательных значениях
называется током насыщения и означает, что все вылетевшие в единицу времени с катода под влиянием света электроны достигли анода. Существование фототока при отрицательных значениях  связана с характеристикой задерживающего электрического поля – задерживающим напряжением
связана с характеристикой задерживающего электрического поля – задерживающим напряжением 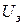 соотношением:
соотношением:  , где
, где 


