
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость движения частиц упругой средыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
- это частная производная от смещения по времени, т.е.
с такой скоростью частицы среды колеблются около своих положений равновесия. Продольные и поперечные волны Обозначим через Фронт волны - поверхность, отделяющая часть пространства, охваченную волновым процессом, от той части, где колебания не возникли. Волновая поверхность - это геометрическое место точек, колеблющихся в одинаковой фазе. Плоская и сферическая волны Плоская волна - волновые поверхности - плоскости. Сферическая волна - волновые поверхности - сферы. В общем случае форма волновых поверхностей может быть любой. Длина волны - это расстояние, на которое распространяется волна за один период колебаний.
Так как (14.1.1.3) То Уравнение плоской волны. Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача – найти
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время
Фаза волны - это аргумент у косинуса в уравнении волны, т.е.
Фаза плоской волны зависит от двух переменных - x и t. Фазовая скорость - это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.
Найдем производную от этого выражения по времени:
откуда искомая фазовая скорость волны:
Уравнение плоской волны, распространяющейся в направлении, противоположном оси x:
Из (15.2.2) для этой волны:
Волновое число, симметричная форма уравнения волны
Введем
Тогда
При такой записи координата х и время t входят в уравнение волны симметрично. Связь волнового числа с длиной волны
Уравнение плоской волны, распространяющейся в произвольном направлении. Волновой вектор
здесь
Волновое уравнение Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:
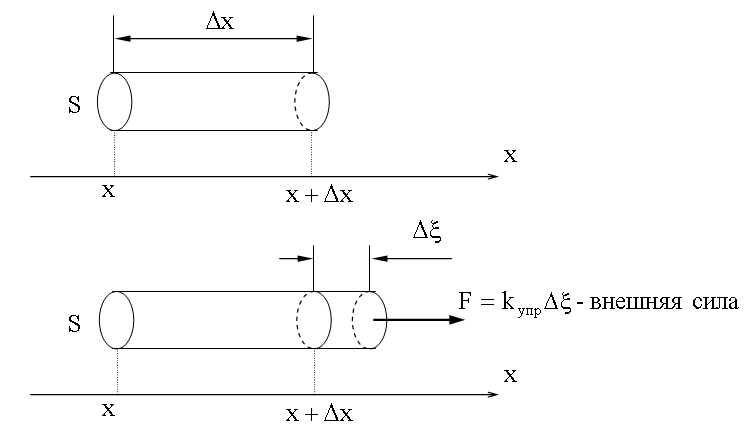
Вывод закона Гука для бесконечно малого упругого стержня Выделим элемент упругого стержня, длиной Δx.
Закрепим левую часть этого элемента (второй рисунок), правую сместим на величину Δξ вдоль оси x.
Здесь коэффициент kупр, характеризующий упругость стержня, зависит от материала стержня, его длины и площади сечения. Нормальное напряжение и относительная деформация Введем:
При Δx → 0
Перепишем, выразив F и Δξ через σ и ε:
или
Модуль Юнга Величина
Закон Гука Тогда связь нормального напряжения σ и относительной деформации ε будет иметь вид:
Это выражение тоже носит название закона Гука.
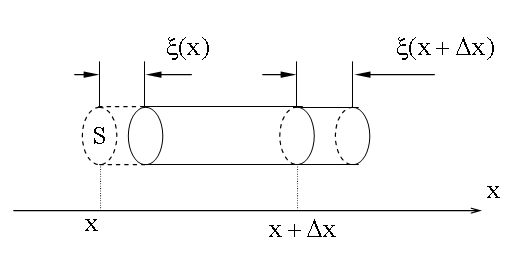
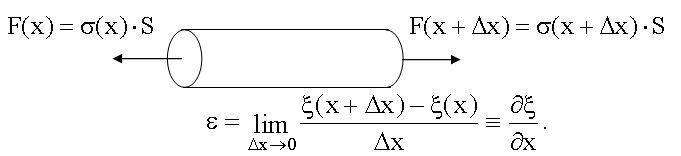
15.3.2. Вывод волнового уравнения из Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.
В нашем примере стержень растянут внешними силами:
Сумма этих сил равна:
Домножим и поделим последнее выражение на Δ x. Величина
при Δx → 0 дает вторую производную от "кси" по x, т.е. Тогда Масса нашего элемента
тогда
или
Проверим, будет ли
Откуда
Т.к.
и волновое уравнение можно записать в виде:
Для волны, распространяющейся в произвольном направлении (15.2.5) волновое уравнение имеет вид:
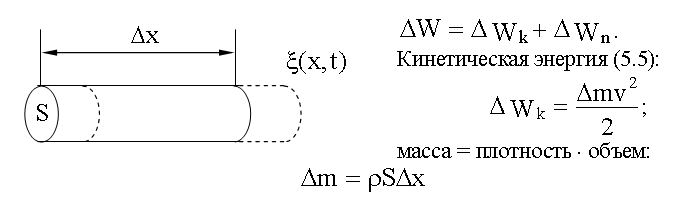
Энергия упругой волны Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:
Скорость (3.8.2):
тогда
Потенциальная энергия упругого деформированного стержня:
Полная энергия выделенного элемента объемом SΔx будет равна:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1093; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.3.236 (0.007 с.) |

 ,
, скорость распространения волны. Если направление смещения
скорость распространения волны. Если направление смещения 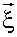 (и скорость частицы
(и скорость частицы  ) совпадают с направлением скорости волны, то волна называется продольной. Если
) совпадают с направлением скорости волны, то волна называется продольной. Если  см. (3.9),
см. (3.9),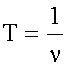 ,
, или
или 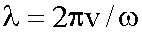 .
.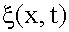 - уравнение волны, если задано
- уравнение волны, если задано 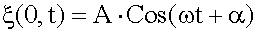 .
.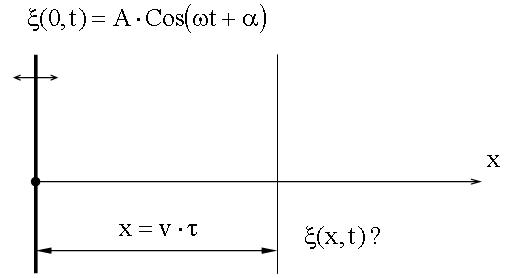
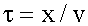 , значит уравнение волны
, значит уравнение волны .
.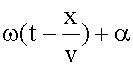 ,
,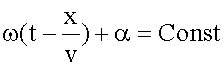 .
.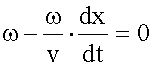 ,
, .
. .
. .
.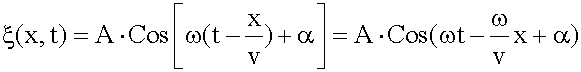 .
. - волновое число.
- волновое число.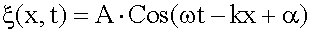 .
.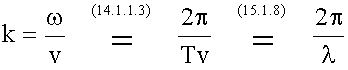 .
.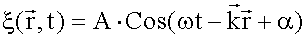 ,
,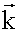 - волновой вектор,
- волновой вектор, - скалярное произведение волнового вектора и радиус-вектора.
- скалярное произведение волнового вектора и радиус-вектора.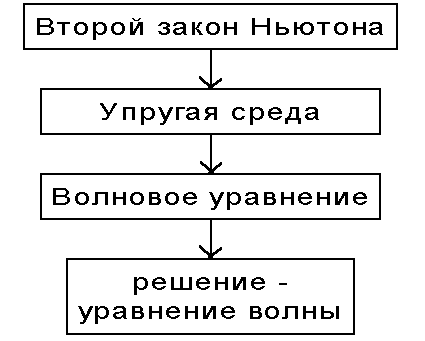
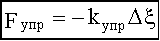 - закон Гука.
- закон Гука.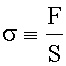 - нормальное напряжение,
- нормальное напряжение,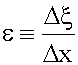 - относительная деформация.
- относительная деформация.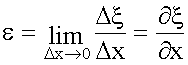 .
.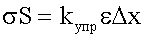
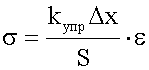 .
.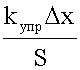 не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:
не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала: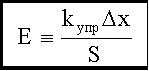 .
.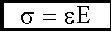 .
.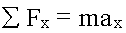 .
. .
.
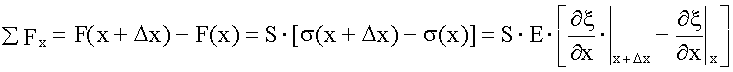 .
.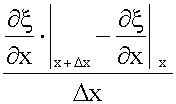
 .
. .
.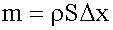 , его ускорение (3.10)
, его ускорение (3.10)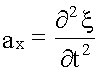 ,
,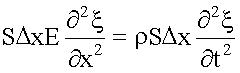 ,
,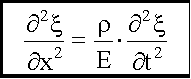 - волновое уравнение.
- волновое уравнение.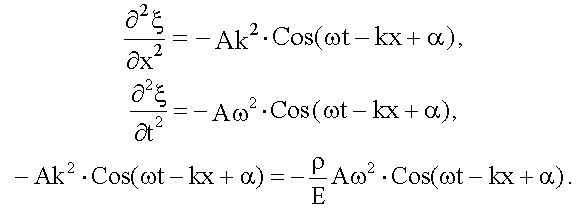
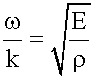 .
.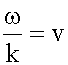 (15.2.4), то фазовая скорость упругой продольной волны:
(15.2.4), то фазовая скорость упругой продольной волны: ,
,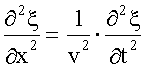 .
. .
. .
.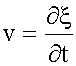 ,
,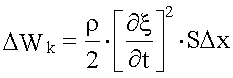 .
. .
. .
.


