
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы отражения и преломленияСодержание книги
Поиск на нашем сайте
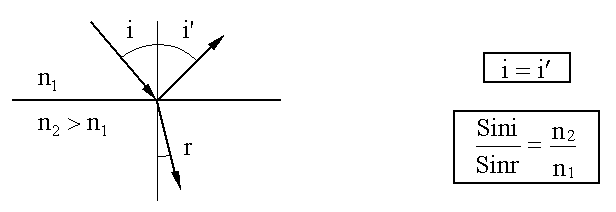
утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим лучом и перпендикуляром, восстановленным к границе раздела в точке падения. Угол падения равен углу отражения. Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления (16.5.2) второй среды к показателю преломления первой.
Законы отражения и преломления могут нарушаться в анизотропных средах, т.е. средах, для которых показатель преломления зависит от направления в пространстве. Полное внутреннее отражение
При увеличении угла падения i, угол преломления тоже увеличивается, при этом интенсивность (16.5.4) отраженного луча растет, а преломленного - падает (их сумма равна интенсивности падающего луча). При каком-то значении i = iкр угол r = π/2, интенсивность преломленного луча станет равной нулю, весь свет отразится. При дальнейшем увеличении угла i > iкр преломленного луча не будет, происходит полное отражение света. Значение критического угла падения, при котором начинается полное отражение найдем, положим в законе преломления r = π/2, тогда Sin r = 1, значит:
Тонкие линзы Линза - система двух, чаще всего сферических, преломляющих поверхностей, ограничивающих прозрачное тело. Обычно линзы делают стеклянными. Собирающие и рассеивающие линзы Линзы бывают собирающими и рассеивающими.
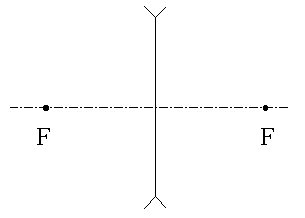
Объясните такой ход лучей в линзах, применяя закон преломления. Линза называется тонкой, если ее толщиной можно пренебречь. Схематически тонкая собирающая линза
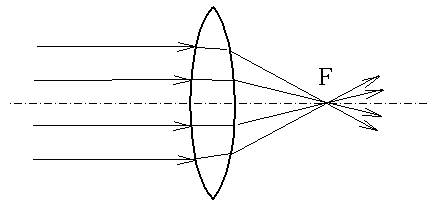
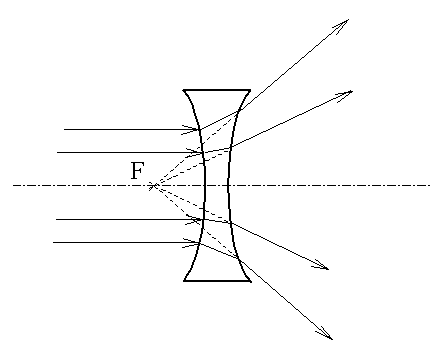
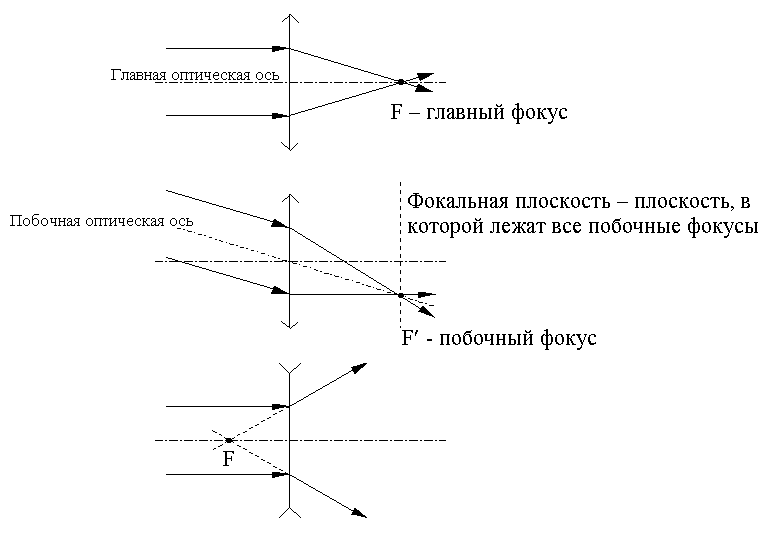
Фокусы линзы, фокальная плоскость Буквой F обозначены фокусы линзы - точки, в которых собираются параллельные оптической оси лучи, прошедшие через линзу (или их продолжения).
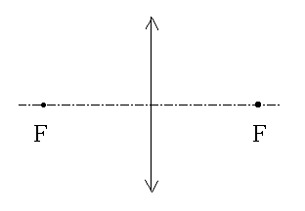
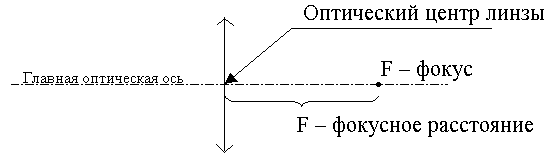
Фокусное расстояние тонкой линзы Буквой F обозначают также и фокусное расстояние линзы - расстояние от фокуса до оптического центра линзы.
Для сферической тонкой линзы на основе закона преломления получается следующая формула для фокусного расстояния:
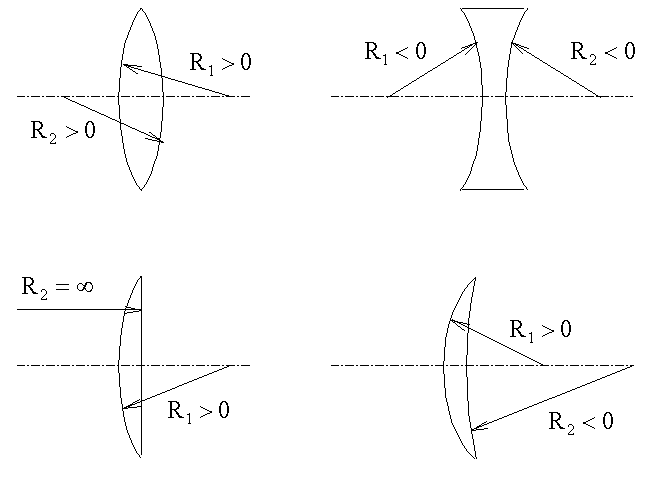
Здесь nл и nср - показатели преломления линзы и среды, соответственно. Эта формула справедлива только для приосевых (параксиальных) лучей. R1, R2 - радиусы кривизны сферических поверхностей линзы могут быть положительными и отрицательными. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутый - отрицательным. Выбор знаков R1 и R2 в приведенной нами формуле для F иллюстрируют следующие рисунки [Следует отметить, что существует и другое, более формальное правило знаков.]):
Для собирающей линзы фокусное расстояние F положительно, для рассеивающей - отрицательно. Оптической силы линзы называют величину Ф, обратную фокусному расстоянию линзы:
Единица оптической силы - диоптрия (дтпр).
Построение изображения в линзах Для построения изображения предмета необходимо построить изображение каждой его точки. Для построения изображения точки достаточно найти точки пересечение двух любых лучей идущих из заданной точки. Удобнее всего использовать в качестве одного из этих лучей луч, идущий через оптический центр, он идет через линзу не отклоняясь:
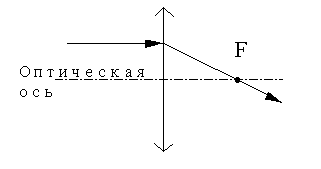
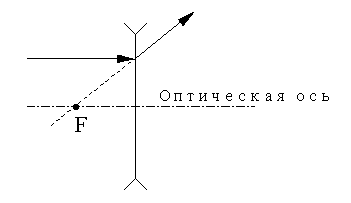
Другой удобный луч - идущий параллельно оптической оси. Он, преломляясь в линзе, проходит через фокус, если линза собирающая:
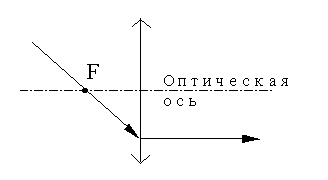
Если линза рассеивающая, то через фокус проходит продолжение луча:
И, если луч шел через фокус собирающей линзы, то после преломления он пойдет параллельно оптической оси:
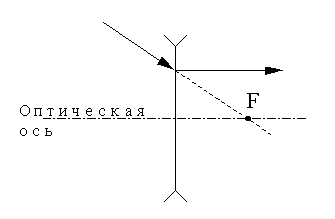
Для рассеивающей линзы параллельно оптической оси пойдет после преломления луч, продолжение которого проходит через фокус:
Примеры построения изображения точки в собирающей линзе
Пример построения изображения точки в рассеивающей линзе
Формула линзы
ΔABO подобен ΔA'B'O, значит:
ΔOCF подобен ΔA'B'F, значит:
освободимся от знаменателя:
поделим на df F, тогда:
или
откуда следует формула тонкой линзы:
Здесь d, f, F - алгебраические величины. ИНТЕРФЕРЕНЦИЯ СВЕТА Интерференция (от лат. Inter - взаимно, ferio - ударяю) - взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве. Интерференция - это одно из основных свойств волн любой природы: упругих (15), электромагнитных (16), в том числе и световых (16.5).
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.201.207 (0.01 с.) |


 .
.
 .
.
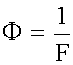 ,
,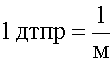 .
.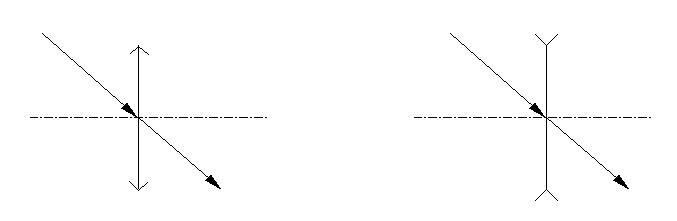




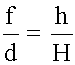 .
.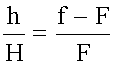 , следовательно:
, следовательно:  ,
,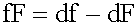 ,
, ,
, ,
, .
.


