Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о колебательных процессахСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие о колебательных процессах Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Примеры колебаний:
Гармонические колебания Гармонические колебания - это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса, либо косинуса:
или
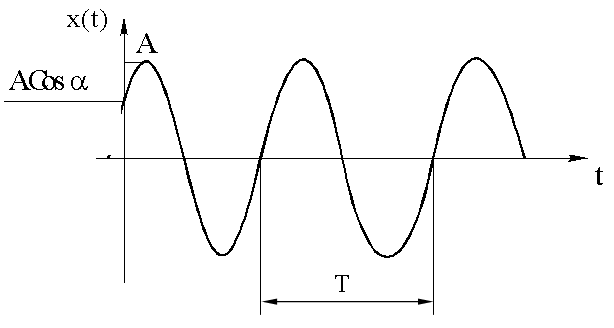
где A - амплитуда; ω - круговая частота; α - начальная фаза; (ωt + α) - фаза. Фаза колебания Фаза колебания - это аргумент гармонической функции: (ωt + α). Начальная фаза α - это значение фазы в начальный момент времени, т.е. при t = 0. Амплитуда колебания Амплитуда колебания A - это наибольшее значение колеблющейся величины. 14.1.1.3. Круговая или циклическая частота ω При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π.
ω (t + T) + α = ωt + α + 2π, или ωT = 2π.
Время T одного полного колебания называется периодом колебания. Частотой ν называют величину, обратную периоду
Единица измерения частоты - герц (Гц), 1 Гц = 1 с-1. Так как
то
Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота - это скорость изменения фазы со временем. Действительно:
График гармонического колебания
Дифференциальное уравнение гармонических колебаний Колеблющиеся системы Рассмотрим колебания в трех системах: а) колебания заряда в колебательном контуре L,C; б) колебания грузика, прикрепленного к пружине; в) колебание физического маятника - любого тела, совершающего колебания вокруг горизонтальной оси, не проходящей через его центр тяжести.
Мы получили дифференциальные уравнения, описывающие движения наших систем. В первых двух случаях уравнения одинаковы по форме, в третьем случае второй член уравнения содержит не φ, а Sin φ. Если рассматривать только малые отклонения маятника от положения равновесия, то тогда, при φ << 1, Sin φ ≈ φ и мы имеем:
Введем обозначения:
Дифференциальное уравнение колебательного движения Для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения
Решение дифференциального уравнения Решением дифференциального уравнения называется функция, обращающая это уравнение в тождество. Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид:
т.е. является гармонической функцией. Значит уравнение Сложение колебаний Векторная диаграмма Векторная диаграмма - это способ графического задания колебательного движения в виде вектора.
Вдоль горизонтальной оси откладывается колеблющаяся величина ξ (любой физической природы). Вектор Сложение колебаний одинаковой частоты и одинакового направления Пусть складывается два колебания:
По теореме косинусов Так как
то
Очевидно (см. диаграмму), что начальная фаза результирующего колебания определяется соотношением:
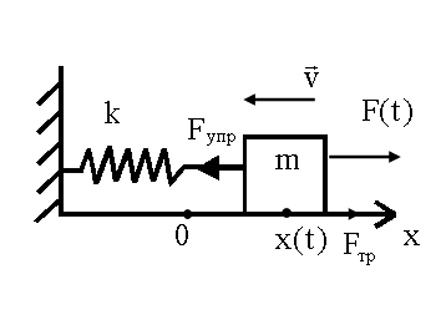
Затухающие колебания Рассмотрим колебания, происходящие в двух системах: а) колебания заряда в колебательном контуре L,C, имеющем активное сопротивление R; б) колебание грузика, прикрепленного к пружинке, учтем влияние трения на движение грузика. Колеблющиеся системы
Решение Каким будет его решение? При Наличие затухания, потерь энергии, переход ее из электромагнитной или механической в тепловую приведет к уменьшению амплитуды колебаний с течением времени, станет другой, меньшей чем ω0, и частота колебаний. Предположим, что амплитуда убывает по экспоненциальному закону, т.е. A(t) = A0·e-βt (e=2,71828...), тогда решение будем искать в виде:
Проверка Выясним, при каких условиях эта функция будет решением, для этого найдем
Сгруппируем члены с косинусом и синусом, на A0e-βt сократим:
Для тождественного обращения левой части в ноль надо, что бы коэффициент при косинусе обращался в ноль (коэффициент при синусе обратился в ноль, т.к. мы "удачно" выбрали A(t) = A0βt. Из этого требования следует выражение для - ω частоты затухающих колебаний.
Период затухающих колебаний
График затухающих колебаний
Время релаксации Время релаксации - это время τ, за которое амплитуда уменьшилась в e=2,7... раз, т.е.
Т.к.
Добротность
Вынужденные колебания Вынужденные колебания - это колебания, происходящие под действием периодического внешнего воздействия.
Векторная диаграмма Изобразим эти колебания с помощью векторов (14.3.1.), амплитуды которых получаются после умножения
В отличие от (14.3.2) вправо направим вектор длиной ω20A, изображающий функцию ω20A · Cos(ωt - φ), начальная фаза которой равна "минус фи".
Резонанс Т.к. то
Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ωрез - резонансной. Для определения ωрез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω). Возьмем от него производную по и приравняем к нулю:
откуда:
При 2β2 > ω20 резонанс отсутствует (ωрез - мнимое число). Амплитуда при резонансе Амплитуда при резонансе получается при подстановке найденного выражения ωрез в формулу для A(ω).
При β << ω0:
При ω = 0 отклонение системы от положения равновесия
Найдем отношение Aрез / A0 при условии β << ω0:
здесь Q - добротность. Добротность показывает (при β << ω0) во сколько раз амплитуда при резонансе больше смещения при ω = 0.
Резонансные кривые График зависимости A(ω) при различных β носят название резонансных кривых.
β1 < β2 < β3, 2β23 > ω20, в этом случае резонанса нет.
15.1. Основные определения Что такое упругая волна? Упругая волна - это процесс распространения колебаний в упругой среде. Характерное свойство волны - перенос энергии без переноса вещества. Описание волны Для описания волны надо ввести функцию, в общем случае - векторную, задающую смещение от положения равновесия каждой частицы упругой среды для любого момента времени. Обозначим эту функцию греческой буквой
Фронт волны - поверхность, отделяющая часть пространства, охваченную волновым процессом, от той части, где колебания не возникли. Волновая поверхность - это геометрическое место точек, колеблющихся в одинаковой фазе. Плоская и сферическая волны Плоская волна - волновые поверхности - плоскости. Сферическая волна - волновые поверхности - сферы. В общем случае форма волновых поверхностей может быть любой. Длина волны - это расстояние, на которое распространяется волна за один период колебаний.
Так как (14.1.1.3) То Уравнение плоской волны. Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача – найти
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время
Фаза волны - это аргумент у косинуса в уравнении волны, т.е.
Фаза плоской волны зависит от двух переменных - x и t. Фазовая скорость - это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.
Найдем производную от этого выражения по времени:
откуда искомая фазовая скорость волны:
Уравнение плоской волны, распространяющейся в направлении, противоположном оси x:
Из (15.2.2) для этой волны:
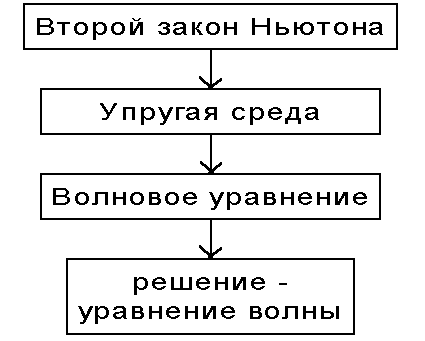
Волновое уравнение Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:
Модуль Юнга Величина
Закон Гука Тогда связь нормального напряжения σ и относительной деформации ε будет иметь вид:
Это выражение тоже носит название закона Гука.
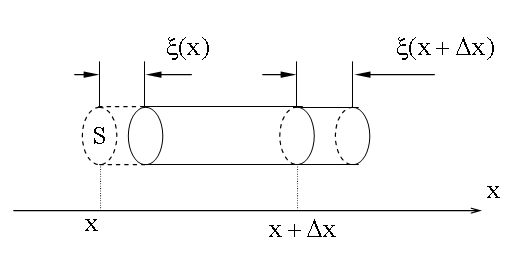
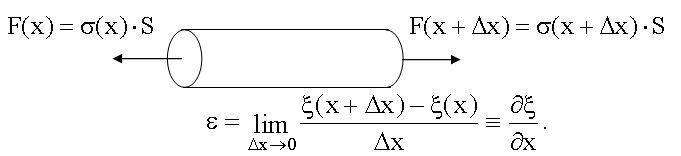
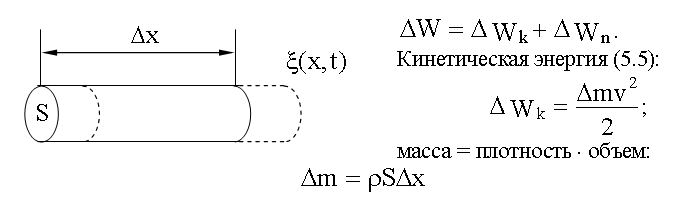
15.3.2. Вывод волнового уравнения из Пусть волна распространяется вдоль упругого стержня. Рассмотрим элемент этого стержня, его длина равна Δx в невозмущенном состоянии. Пусть при распространения волны левая часть этого элемента сместится на величину ξ(x), а правая - на величину ξ(x + Δx), не равную смещению левой части.
В нашем примере стержень растянут внешними силами:
Сумма этих сил равна:
Домножим и поделим последнее выражение на Δ x. Величина
при Δx → 0 дает вторую производную от "кси" по x, т.е. Тогда Масса нашего элемента
тогда
или
Проверим, будет ли
Откуда
Т.к.
и волновое уравнение можно записать в виде:
Для волны, распространяющейся в произвольном направлении (15.2.5) волновое уравнение имеет вид:
Энергия упругой волны Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:
Скорость (3.8.2):
тогда
Потенциальная энергия упругого деформированного стержня:
Полная энергия выделенного элемента объемом SΔx будет равна:
Поток энергии
Плотность потока энергии
Интенсивность волны - это среднее по времени от модуля вектора плотности потока энергии:
Для гармонической волны:
Стоячие волны При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит. Уравнение стоячей волны Для волны, бегущей по оси x:
Для волны, бегущей против оси x:
Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:
Амплитуда стоячей волны - это модуль выражения, стоящего перед множителем Cosωt, т.е.
Узлы и пучности Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:
Следовательно, координаты узлов:
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны. Для пучностей:
Координаты пучностей:
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ Выпишем здесь еще раз систему уравнений Максвелла в дифференциальной форме вместе с материальными уравнениями (15.3):
Применим систему уравнений Максвелла (13.4) к однородной (ε = const, μ = const), нейтральной (ρ = 0), непроводящей (σ = 0) среде. Уравнения Максвелла примут следующий вид. Первая пара:
Вторая пара:
Наша задача - получить волновые уравнения для векторов Волновое уравнение В уравнения (2) и (7) входят Ez и Hy, в уравнения (3) и (6) входят Ey и Hz. Таким образом, если первоначально было создано поле Ey, то оно породит Hz (3), которое создает Ey (6). Аналогично с Ez и Hy. Для описания электромагнитной волны можно выбрать уравнения (2) и (7), либо уравнения (3) и (6), либо те и другие. Получим волновое уравнение для уравнений (3) и (6):
После указанных стрелками замен имеем два волновых уравнения:
Диполь - это два разноименных точечных заряда, находящихся на некотором расстоянии друг от друга
Световые волны Световая волна - это электромагнитная волна с длиной волны в вакууме:
Волны такого диапазона воспринимаются человеческим глазом. Частота световой волны (15.1.8.), (16.1.2.1.):
Показатель преломления Скорость распространения света в среде, как и любой электромагнитной волны, см. (16.2):
где
Дисперсия Т.к. зависит от частоты электромагнитной волны (см. 9.13), то n = n(v) или n = n(λ) - показатель преломления будет зависеть от длины волны света. Световой вектор - это вектор напряженности электрического поля световой (электромагнитной!) волны.
16.5.4. Интенсивность света. Для любой электромагнитной волны:
Для световой волны:
откуда
Значит интенсивность световой волны:
Испускание света атомами Атом, при переходе электрона в состояние с более низкой энергией, испускает фотон, которому соответствует электромагнитная волна, протяженностью ~3 метра. Это соответствует длительности процесса излучения ~10-8 секунды. Такая электромагнитная волна называется цугом.
Естественный свет Каждый цуг имеет вполне определенное направление светового вектора Световая волна, испускаемая нагретым телом, складывается из огромного числа цугов, испускаемых атомами тела. Атомы нагретого тела испускают несогласованные цуги, направление векторов
ГЕОМЕТРИЧЕСКАЯ ОПТИКА Это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий - лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что λ → 0. Геометрическая оптика позволяет во многих случаях достаточно хорошо рассчитать оптическую систему. Но в ряде случаев реальный расчет оптических систем требует учета волновой природы света, расчет в рамках геометрической оптики дает приближенный результат, иногда неверный даже на качественном уровне. Полное внутреннее отражение
При увеличении угла падения i, угол преломления тоже увеличивается, при этом интенсивность (16.5.4) отраженного луча растет, а преломленного - падает (их сумма равна интенсивности падающего луча). При каком-то значении i = iкр угол r = π/2, интенсивность преломленного луча станет равной нулю, весь свет отразится. При дальнейшем увеличении угла i > iкр преломленного луча не будет, происходит полное отражение света. Значение критического угла падения, при котором начинается полное отражение найдем, положим в законе преломления r = π/2, тогда Sin r = 1, значит:
Тонкие линзы Линза - система двух, чаще всего сферических, преломляющих поверхностей, ограничивающих прозрачное тело. Обычно линзы делают стеклянными. Примеры построения изображения точки в собирающей линзе
Пример построения изображения точки в рассеивающей линзе
Формула линзы
ΔABO подобен ΔA'B'O, значит:
ΔOCF подобен ΔA'B'F, значит:
освободимся от знаменателя:
поделим на df F, тогда:
или
откуда следует формула тонкой линзы:
Здесь d, f, F - алгебраические величины. ИНТЕРФЕРЕНЦИЯ СВЕТА Интерференция (от лат. Inter - взаимно, ferio - ударяю) - взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве. Интерференция - это одно из основных свойств волн любой природы: упругих (15), электромагнитных (16), в том числе и световых (16.5). Когерентные волны Когерентные световые волны получают, разделив волну от одного источника на две. Эти две части одной волны уже будут когерентны (α1 = α2, в пределах каждого цуга). Тогда <Cosδ> = Cosδ = const, при фиксированных r1 и r2, следовательно:
Пусть для простоты, начальные фазы α1 и α2 интерферирующих волн равны нулю, тогда:
здесь λ0 = cT - длина световой волны в вакууме. Оптической разностью хода называют величину:
Тогда:
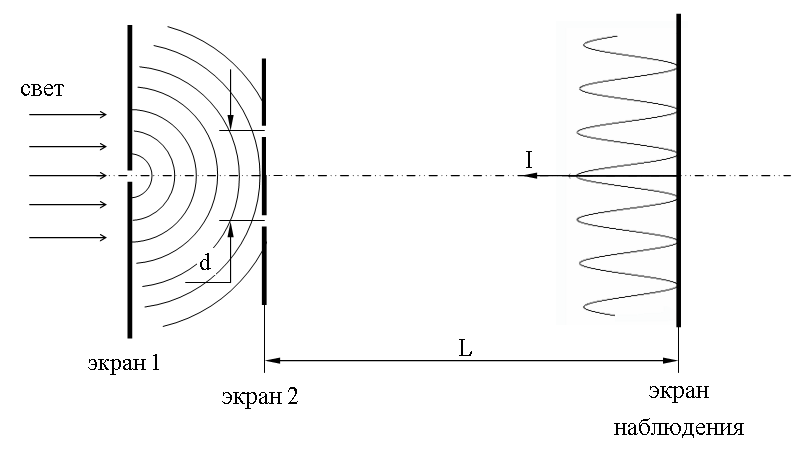
Опыт Юнга Томас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране.
Интерференционная картина наблюдалась на экране, удаленном на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн. При использовании лазера в качестве источника света необходимость в экране отпадает.
Свет от узкой щели S падает на два плоских зеркала, развернутых друг относительно друга на очень малый угол φ. Используя закон отражения света (17.1.3.) нетрудно показать, что падающий пучок света разобьется на два, исходящих из мнимых источников S1 и S2. Источник S закрывают от экрана наблюдения непрозрачным экраном.
Две стеклянные призмы с малым преломляющим углом θ изготавливают из одного куска стекла так, что призмы сложены своими основаниями, Источник света - ярко освещенная щель S. После преломления в бипризме падающий пучок расщепляется на два, исходящих от мнимых источников S1 и S2, которые дают две когерентные цилиндрические волны. Так как преломляющий угол θ мал, то все лучи отклоняются каждой из половинок бипризмы на один и тот же угол φ. Можно показать, что в этом случае
здесь n - показатель преломления материала призмы. Расстояние между источниками:
Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.
Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает. При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды. Для n1 = 1 и n3 > n2 оптическая разность хода Δ = n2S2 - S1. После преобразований с учетом закона преломления и тригонометрических формул получим:.
Если n3 < n2, тогда:
Здесь λ0/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A. Связь разности фаз δ и разности хода Δ, см. (18.1.2.2.).
Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r - радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0. Тогда геометрическая разность хода с большой точностью равна 2b. При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений.
Если в зазоре между линзой и пластиной n = 1, то для радиуса интерференционных полос (колец Ньютона) получается формула:
При четном m кольца Ньютона темные, в частности при m = 0, r = 0 и в центре наблюдается темное пятно (из-за потери λ0/2 при отражении от стеклянной пластинки). Если m нечетное, то кольца с
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1006; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.124 (0.014 с.) |

 ,
,
 .
.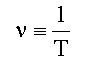 .
. ,
, .
.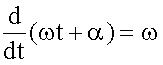 .
.





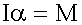



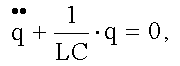


 .
. ,
,
 ,
,
 ,
,
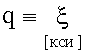 ,
,
 ,
,
 .
.
 .
. ,
,


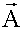 , отложенный из точки 0 равен по модулю амплитуде колебания A и направлен под углом α, равным начальной фазе колебания, к оси ξ. Если привести этот вектор во вращение с угловой скоростью ω, равной циклической частоте колебаний, то проекция этого вектора на ось ξ дает значение колеблющейся величины в произвольный момент времени.
, отложенный из точки 0 равен по модулю амплитуде колебания A и направлен под углом α, равным начальной фазе колебания, к оси ξ. Если привести этот вектор во вращение с угловой скоростью ω, равной циклической частоте колебаний, то проекция этого вектора на ось ξ дает значение колеблющейся величины в произвольный момент времени.

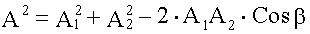 .
. ,
, .
. .
.







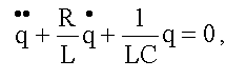



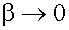 (отсутствие сопротивления, трения) оно должно переходить в
(отсутствие сопротивления, трения) оно должно переходить в  (см. 14.2).
(см. 14.2). .
. и подставим в дифференциальное уравнение.
и подставим в дифференциальное уравнение.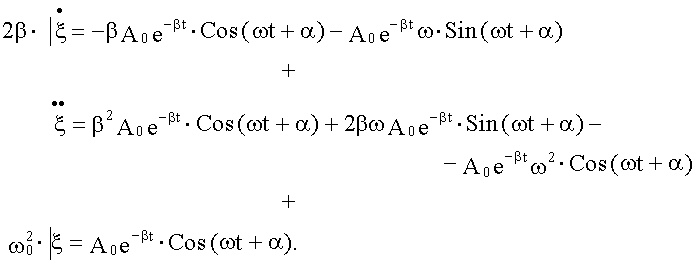
 .
.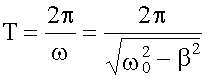 .
.
 , тогда
, тогда  .
. .
. - число колебаний за время, то:
- число колебаний за время, то: .
.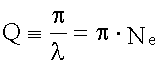 .
.
 .
.
 .
.


 ,
,
 .
.
 ;
;
 .
.


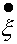 на 2β, а - ξ на ω20.
на 2β, а - ξ на ω20. .
.
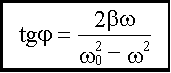
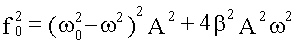 ,
,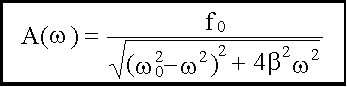 .
.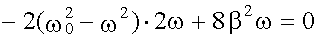 ,
,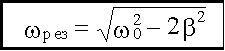 .
.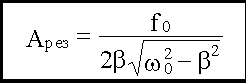 .
. .
.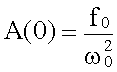 .
. ,
,
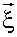 [кси]. Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-вектор), и время t, т.е.
[кси]. Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-вектор), и время t, т.е. .
. см. (3.9),
см. (3.9),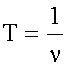 ,
, или
или 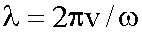 .
.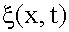 - уравнение волны, если задано
- уравнение волны, если задано 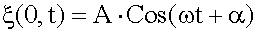 .
.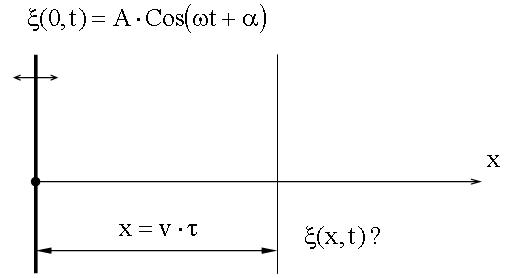
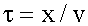 , значит уравнение волны
, значит уравнение волны .
.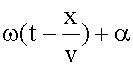 ,
,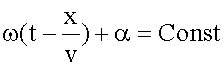 .
.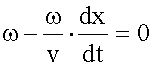 ,
, .
. .
. .
.
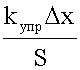 не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:
не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала: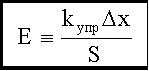 .
.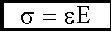 .
.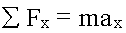 .
. .
.
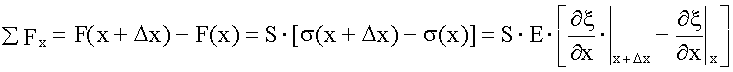 .
.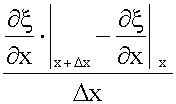
 .
. .
.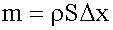 , его ускорение (3.10)
, его ускорение (3.10)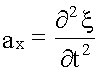 ,
,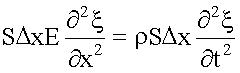 ,
,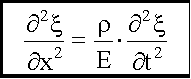 - волновое уравнение.
- волновое уравнение.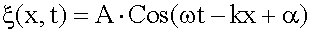 его решением.
его решением.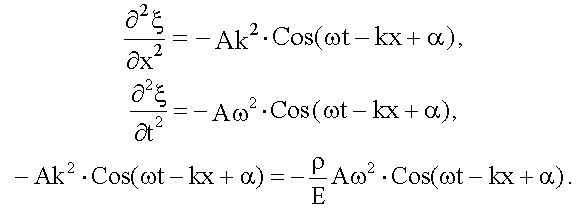
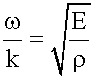 .
.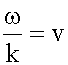 (15.2.4), то фазовая скорость упругой продольной волны:
(15.2.4), то фазовая скорость упругой продольной волны: ,
,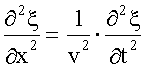 .
. .
. .
.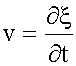 ,
,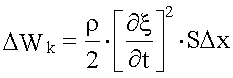 .
. .
. .
.

 .
. .
. .
. , см. (15.2.3), (15.2.4), (15.2.5).
, см. (15.2.3), (15.2.4), (15.2.5).








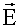 и
и  , решениями которых будут уравнения электромагнитной волны
, решениями которых будут уравнения электромагнитной волны  (сравните с 15.3).
(сравните с 15.3).




 ,
, - показатель преломления среды, т.к. μ = 1 для большинства прозрачных веществ.
- показатель преломления среды, т.к. μ = 1 для большинства прозрачных веществ. , см. (16.3.2).
, см. (16.3.2). , см. (16.1.2.3),
, см. (16.1.2.3), .
. .
.


 .
.



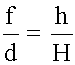 .
.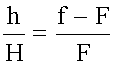 , следовательно:
, следовательно:  ,
,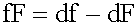 ,
, ,
, ,
, .
.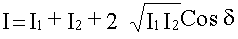 .
.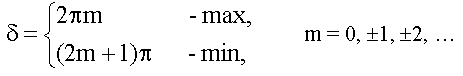
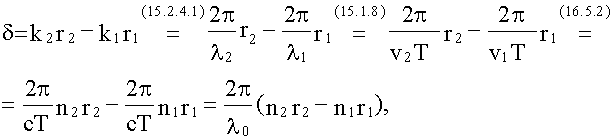
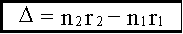 .
.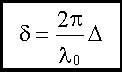 .
.

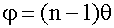 ,
, .
.

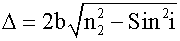 .
. .
.