
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частота затухающих колебанийСодержание книги
Поиск на нашем сайте
Период затухающих колебаний
График затухающих колебаний
Переход к апериодическому движению При увеличении коэффициента затухания β период затухающих колебаний (14.4.9) растет, при β → ω0 период T → ∞. При β > ω0 периодическое решение у дифференциального уравнения затухающих колебаний отсутствует:
Логарифмический декремент затухания
подставим A(t) = A0-βt.
Время релаксации Время релаксации - это время τ, за которое амплитуда уменьшилась в e=2,7... раз, т.е.
Т.к.
Добротность
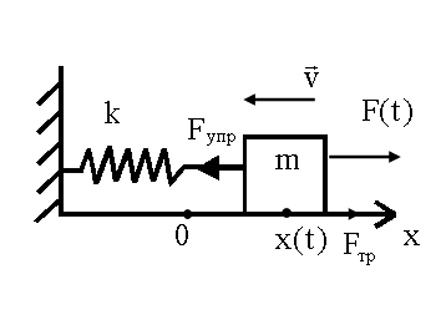
Вынужденные колебания Вынужденные колебания - это колебания, происходящие под действием периодического внешнего воздействия.
Дифференциальное уравнение, описывающее вынужденные колебания наших двух систем будет иметь один и тот же вид:
Решение дифференциального уравнения Решение дифференциального уравнения вынужденных колебаний - ξ(t) - состоит из двух слагаемых:
здесь ξ1(t) - общее решение однородного уравнения, т.е. уравнения с нулем в правой части (см. 14.4.5.), ξ2(t) - частное решение неоднородного уравнения, т.е. уравнения с ненулевой правой частью - (14.5.5)
здесь - ξ1(t) убывает с течением времени и его роль существенна при переходных процессах. Стационарное, установившееся значение ξ(t) определяется, в основном, слагаемым ξ2(t). Наша задача - найти ξ2(t).
Частное решение неоднородного уравнения Частное решение неоднородного уравнения - ξ2(t). Ищем ξ2(t) в виде гармонической функции изменяющейся с частотой внешнего воздействия ω:
Первая и вторая производные от этой функции также будут гармоническими функциями, изменяющиеся с частотой ω. Значит, в уравнении 14.5.3.5, в левой его части, будет сумма трех гармонических функций одинаковой частоты, справа - гармоническая функция той же частоты, т.е. сумма трех колебаний одной частоты равна четвертому колебанию той же частоты. Задачу о сложении колебаний мы решим методом векторных диаграмм (14.3.1.), для этого
Векторная диаграмма Изобразим эти колебания с помощью векторов (14.3.1.), амплитуды которых получаются после умножения
В отличие от (14.3.2) вправо направим вектор длиной ω20A, изображающий функцию ω20A · Cos(ωt - φ), начальная фаза которой равна "минус фи".
Резонанс Т.к. то
Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ωрез - резонансной. Для определения ωрез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω). Возьмем от него производную по и приравняем к нулю:
откуда:
При 2β2 > ω20 резонанс отсутствует (ωрез - мнимое число). Амплитуда при резонансе Амплитуда при резонансе получается при подстановке найденного выражения ωрез в формулу для A(ω).
При β << ω0:
При ω = 0 отклонение системы от положения равновесия
Найдем отношение Aрез / A0 при условии β << ω0:
здесь Q - добротность. Добротность показывает (при β << ω0) во сколько раз амплитуда при резонансе больше смещения при ω = 0.
Резонансные кривые График зависимости A(ω) при различных β носят название резонансных кривых.
β1 < β2 < β3, 2β23 > ω20, в этом случае резонанса нет.
15.1. Основные определения Что такое упругая волна? Упругая волна - это процесс распространения колебаний в упругой среде. Характерное свойство волны - перенос энергии без переноса вещества. Описание волны Для описания волны надо ввести функцию, в общем случае - векторную, задающую смещение от положения равновесия каждой частицы упругой среды для любого момента времени. Обозначим эту функцию греческой буквой
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.008 с.) |

 .
.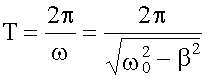 .
.

 ,
, .
. , тогда
, тогда  .
. .
. - число колебаний за время, то:
- число колебаний за время, то: .
.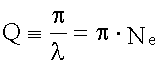 .
.
 .
.
 .
.
 .
.
 .
.


 ,
,
 .
.
 ;
;
 .
.


 .
. ,
, - из (14.4.6),
- из (14.4.6), - частота затухающих колебаний.
- частота затухающих колебаний. .
.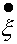 и
и  , после нахождения этих производных, запишем с помощью функции косинуса:
, после нахождения этих производных, запишем с помощью функции косинуса: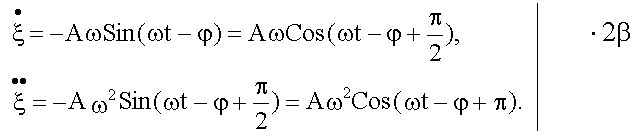 .
. .
.
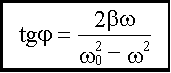
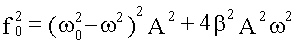 ,
,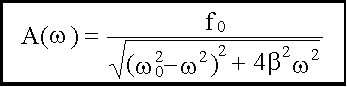 .
.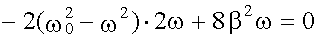 ,
,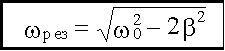 .
.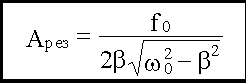 .
. .
.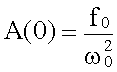 .
. ,
,
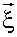 [кси]. Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-вектор), и время t, т.е.
[кси]. Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-вектор), и время t, т.е. .
.


