
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции дипольного момента и напряженности поля волны на ось xСодержание книги
Поиск на нашем сайте
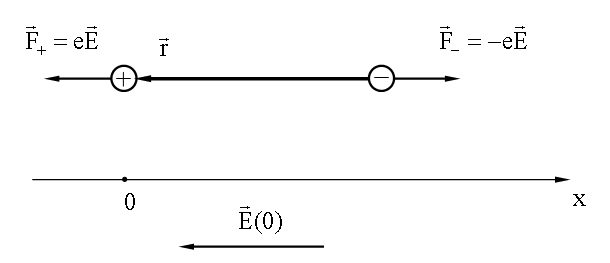
На следующем рисунке изображен диполь, силы действующие на его полюсы, ось x и вектор электрического поля волны в момент времени t = 0:
Как видно из рисунка, проекция дипольного момента (21.1.1.2.1) на ось x:
Проекция напряженности электрического поля световой волны на ось x:
знак минус означает, что в начальный момент времени вектор
21.1.1.3. Выражение для n2 Подставим в формулу, полученную в (21.1.1.2) для n2, выражения px(t), Nx(t) с использованием для x(t) решения уравнения движения, записанное в (21.1.1.2.2):
При усреднении по времени
21.1.1.4. Анализ зависимости n(ω) Как показывает опыт затухание оказывает незначительное влияние на движение оптического электрона, если частота световой волны не равна ω0 - собственной частоте колебаний электрона. Точнее, затуханием можно пренебречь, если
При выполнении этого условия
В первом случае (если ω < ω0) колебания электрона происходят в фазе с вынуждающей силой, Cosφ = 1. Во втором (ω > ω0) - в противофазе, Cosφ = -1. Учитывая это можно записать упрощенное выражение для n2, применимое для частот далеких от ω0:
Здесь знак второго слагаемого при ω < ω0 положителен, при ω > ω0 второе слагаемое отрицательное. Для ω = ω0 φ = π/2, а Cosφ = 0, тогда, возвращаясь к исходному выражению для n2 (20.1.1.3), получим: n = 1.
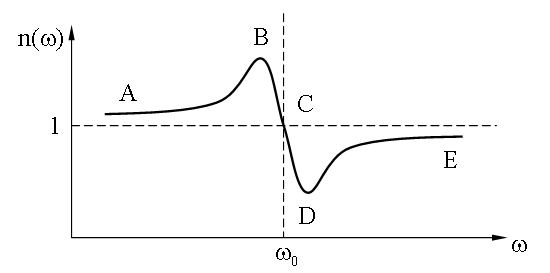
21.1.1.5. График зависимости n(ω) Проведенный анализ позволяет изобразить примерный вид графика зависимости показателя преломления от циклической частоты:
На участках AB и DE n растет с ростом ω - дисперсия нормальная. На участке BCD дисперсия аномальная - с ростом показатель преломления падает.
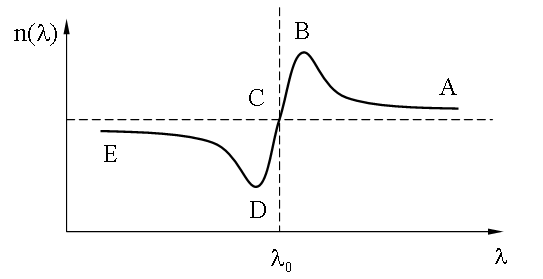
21.1.1.2.6. График зависимости n(λ) Так как длина волны λ и циклическая частота величины, связанные обратно пропорциональной зависимостью (15.1.8), то график n(λ), соответствующий приведенному выше графику, будет иметь примерно следующий вид:
Учет колебаний с другими собственными частотами В веществе могут быть заряды, колеблющиеся с различными собственными частотами ω0 и затуханиями βi, величины зарядов qi могут быть разными, разными могут быть и их массы. С учетом этого формула для n2 примет следующий вид:
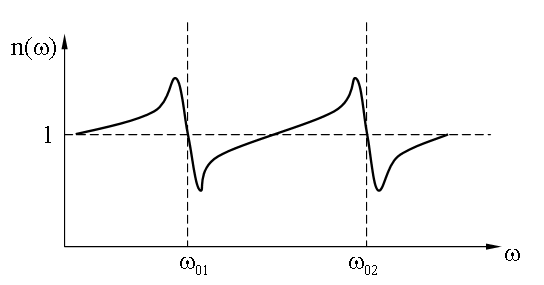
График зависимости n(ω) при наличии двух собственных частот (N = 2) будет иметь следующий вид:
Опыт подтверждает такой ход зависимости n(ω).
Групповая скорость На графике зависимости n(λ), изображенном в 21.1.1, есть участок CDE, где n < 1. Это означает, что фазовая скорость световой волны:
На первый взгляд это утверждение противоречит теории относительности (см. раздел 8), согласно которой скорость света в вакууме является максимально возможной скоростью передачи сигнала. Но монохроматическая волна не может передавать сигнал: она никогда не кончается и нигде не начинается. Такая волна состоит из бесконечно повторяющихся одинаковых горбов и впадин, ничем не отличающихся друг от друга. Передавать сигнал можно только ограниченным в пространстве и во времени кусочком электромагнитной волны - электромагнитным импульсом. Такой импульс (группа волн) можно представить в виде наложения бесконечного числа монохроматических волн с разными частотами и амплитудами (интеграл Фурье). Мы, для простоты будем представлять импульс (группу волн) совокупностью двух близких по частоте монохроматических волн:
Здесь мы во втором сомножителе пренебрегаем величинами Δω и Δk по сравнению с ω и k. Выражение стоящее в квадратных скобках медленно меняется в пространстве и во времени, т. к. Δω << ω, Δk << k (сравните с 14.3.3). Обозначим его буквой A,
Тогда можно считать, что наш импульс (группа волн) - это монохроматическая волна с медленно меняющейся амплитудой:
Будем следить за распространением в пространстве точки xm, где амплитуда A максимальна. Назовем групповой скоростью u скорость перемещения в пространстве точки с координатой xm:
Максимуму A соответствует обращение в ноль фазы косинуса в выражении для A, т.е.
Возьмем производную по времени от этого выражения, в результате получим:
откуда
Переходя к пределу, получим окончательное выражение для групповой скорости:
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.218.229 (0.009 с.) |

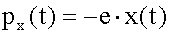 .
. ,
,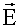 направлен против оси x. Напомним, что в нашем уравнении движения (21.1.1.2.2) сила, действующая на электрон, при t = 0 имеет положительный знак.
направлен против оси x. Напомним, что в нашем уравнении движения (21.1.1.2.2) сила, действующая на электрон, при t = 0 имеет положительный знак.
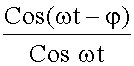 дает
дает  . Подставляя выражение для амплитуды A -колебаний электрона (из 21.1.1.2.1) получим:
. Подставляя выражение для амплитуды A -колебаний электрона (из 21.1.1.2.1) получим: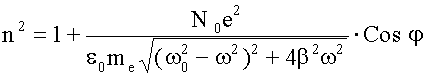 ;
;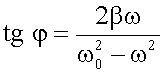 .
.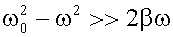 .
.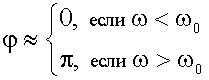 .
. .
.
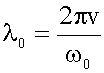 .
.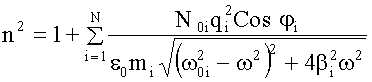 .
.
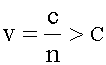 на участке CDE.
на участке CDE.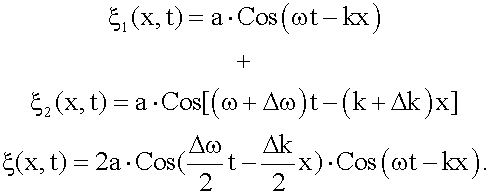
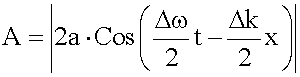 .
.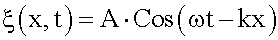 .
. .
.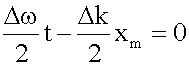 .
.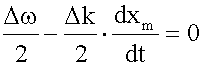 ,
,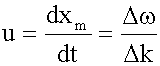 .
. .
.


