Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность энергии упругой волныСодержание книги
Поиск на нашем сайте
Плотность энергии упругой гармонической волны
Среднее по времени значение плотности энергии упругой гармонической волны
Поток энергии
Плотность потока энергии
Вектор Умова - связь плотности потока энергии с плотностью энергии упругой волны
Интенсивность волны - это среднее по времени от модуля вектора плотности потока энергии:
Для гармонической волны:
Стоячие волны При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит. Уравнение стоячей волны Для волны, бегущей по оси x:
Для волны, бегущей против оси x:
Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:
Амплитуда стоячей волны - это модуль выражения, стоящего перед множителем Cosωt, т.е.
Узлы и пучности Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:
Следовательно, координаты узлов:
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны. Для пучностей:
Координаты пучностей:
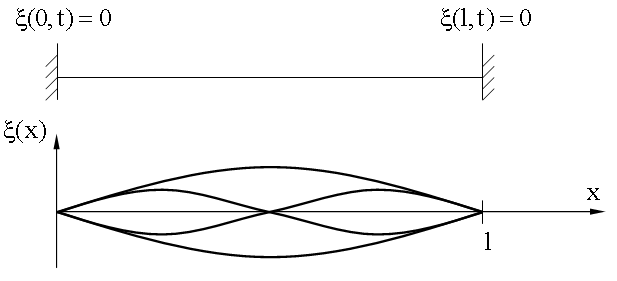
Колебания струны, закрепленной с двух концов
В силу граничных условий, заданных закреплением концов струны, уравнение стоячей волны при выборе начала координат на одном из концов струны следует записать через функцию Sin kx, т.е.
Тогда условие
Это приводит к квантованию волнового числа, т.е. k может принимать не любые значения, а только дискретные, определяемые равенством:
т.к.
то
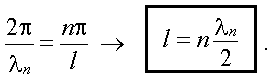
Вдоль струны должно укладываться целое число полуволн! Из (15.1.7)
Частота v1 называется основным током, v2 - первым обертоном и т.д.
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ Выпишем здесь еще раз систему уравнений Максвелла в дифференциальной форме вместе с материальными уравнениями (15.3):
Применим систему уравнений Максвелла (13.4) к однородной (ε = const, μ = const), нейтральной (ρ = 0), непроводящей (σ = 0) среде. Уравнения Максвелла примут следующий вид. Первая пара:
Вторая пара:
Наша задача - получить волновые уравнения для векторов Система уравнений Максвелла для плоской электромагнитной волны Зададим направление оси x перпендикулярно волновым поверхностям. Тогда:
От координат x и z в плоской волне
Учитывая, что
получим три скалярных уравнения:
Второе уравнение первой пары дает:
Аналогично, из второй пары уравнений Максвелла получим:
Поперечность электромагнитных волн Уравнения (1) и (4), (5) и (8) утверждают, что Hx и Ex не зависят от времени и координаты x, т.е. являются однородными постоянными полями. Таким образом, переменное поле электромагнитной волны не имеет составляющей вдоль оси x, в направлении которой распространяется волна. Это значит, что электромагнитная волна поперечна, т.е. векторы и перпендикулярны направлению ее распространения. Волновое уравнение В уравнения (2) и (7) входят Ez и Hy, в уравнения (3) и (6) входят Ey и Hz. Таким образом, если первоначально было создано поле Ey, то оно породит Hz (3), которое создает Ey (6). Аналогично с Ez и Hy. Для описания электромагнитной волны можно выбрать уравнения (2) и (7), либо уравнения (3) и (6), либо те и другие. Получим волновое уравнение для уравнений (3) и (6):
После указанных стрелками замен имеем два волновых уравнения:
Фазовая скорость электромагнитной волны Коэффициент при второй производной по времени, есть величина, обратная квадрату фазовой скорости волны (см. 15.3.2). Для электромагнитной волны фазовая скорость из волновых уравнений 16.1.2:
В вакууме ε = μ = 1 и
Тогда:
Полученное значение фазовой скорости электромагнитной волны в вакууме равно скорости света в вакууме - с. С учетом этого:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.200.16 (0.007 с.) |

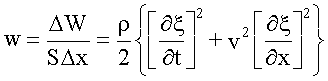 .
.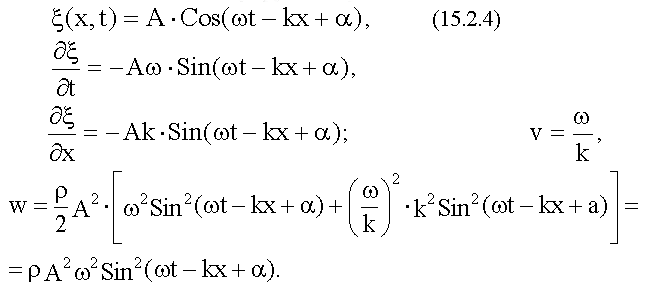
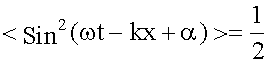 , это известно из математики, значит:
, это известно из математики, значит: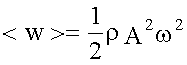 .
.


 .
. .
. .
. , см. (15.2.3), (15.2.4), (15.2.5).
, см. (15.2.3), (15.2.4), (15.2.5).





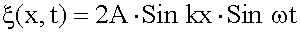 .
.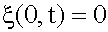 будет выполнено. Для выполнения граничного условия на другом конце струны
будет выполнено. Для выполнения граничного условия на другом конце струны 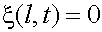 мы должны потребовать, чтобы
мы должны потребовать, чтобы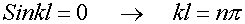 .
.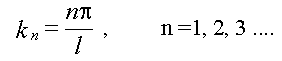
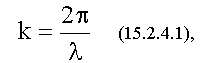
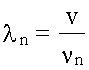 и мы получаем спектр (набор) частот, на которых может колебаться закрепленная с двух концов струна:
и мы получаем спектр (набор) частот, на которых может колебаться закрепленная с двух концов струна: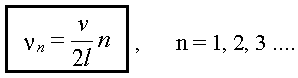



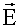 и
и  , решениями которых будут уравнения электромагнитной волны
, решениями которых будут уравнения электромагнитной волны  (сравните с 15.3).
(сравните с 15.3).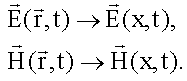
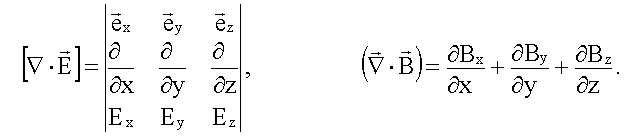
 ,
,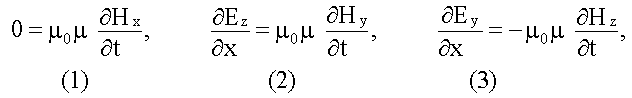
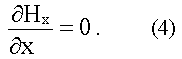
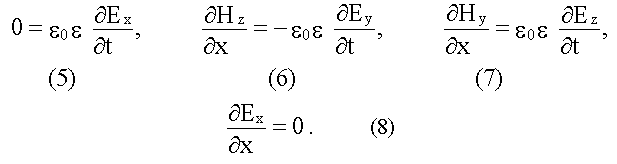


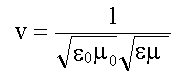
 .
.