
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебательный контур. Превращение энергии в колебательном контуреСодержание книги
Поиск на нашем сайте
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания Резонансная частота контура определяется так называемой формулой Томсона:
Параллельный колебательный контур Пусть конденсатор ёмкостью C заряжен до напряжения. Энергия, запасённая в конденсаторе составляет
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре. В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром. Свободные электромагнитные колебания, их характеристики. Уравнение свободных гармонических колебаний и его решение. Свободными называют колебания, происходящие в системе под действием внутренних сил после вывода системы из положения равновесия. Они заключаются в периодическом изменении следующих величин: заряда q и напряжения U на обкладках конденсатора, напряженности Е и энергии W электрического поля внутри конденсатора, силы тока I в катушке, индукции В и энергии Wm магнитного поля в катушке. Если пренебречь сопротивлением контура, то каждая из величин q, U, E, I, В совершает гармонические колебания, например: Затухающими электромагнитными колебаниями называют колебания в системах с сопротивлением. Скорость затухания колебаний обусловлена силой сопротивления. Затухающие колебания не являются гармоническими.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.176.111 (0.009 с.) |



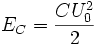 При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю. где
где  — индуктивность катушки,
— индуктивность катушки,  — максимальное значение тока.
— максимальное значение тока. .
.

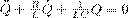 Учитывая формулу собственной частоты колебательного контура и принимая коэффициент затухания равным
Учитывая формулу собственной частоты колебательного контура и принимая коэффициент затухания равным  дифференциальное уравнение колебаний заряда можно записать в виде
дифференциальное уравнение колебаний заряда можно записать в виде  Из зависимостей (1) следует, что колебания заряда подчиняются закону
Из зависимостей (1) следует, что колебания заряда подчиняются закону  (12) с частотой, равной
(12) с частотой, равной 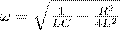 (13)меньшей собственной частоты контура ω0. При R=0:
(13)меньшей собственной частоты контура ω0. При R=0:  (14).
(14).


