
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд. Электризация тел. Закон сохранения электрического заряда. Закон кулона. Точечный заряд.Содержание книги
Поиск на нашем сайте
Электрический заряд. Электризация тел. Закон сохранения электрического заряда. Закон Кулона. Точечный заряд. Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы. Все тела в природе способны электризоваться, т. е. приобретать электрический заряд. Электрический заряд — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материальной точки, является физической абстракцией. Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними: где F12 — сила, действующая на заряд Q1 со стороны заряда Q2, r12 — радиус-вектор, соединяющий заряд Q2 с зарядом Q1, r = |r12|. На заряд Q2 со стороны заряда Q1 действует сила F21 = –F12. Напряжённость электростатического поля. Принцип суперпозиции полей. Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиус-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду. Формула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности. Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов. Циркуляция вектора напряжённости электростатического поля. Работа электростатического поля. Потенциал – энергетическая характеристика электростатического поля. Циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю. Это утверждение выражает теорему о циркуляции электростатического поля. При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Потенциал – энергетическая характеристика электрического поля равен отношению потенциальной энергии заряда в поле к этому заряду. Правила Кирхгофа. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Например, для рисунка (1) первое правило Кирхгофа запишется так:
Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными. Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре: Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома, можно записать: Складывая почленно эти уравнения, получим второе правило Кирхгофа: При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному. 2. Выбрать направление обхода контура и строго его придерживаться; произведение IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, ЭДС, действующие по выбранному направлению обхода, считаются положительными, против — отрицательными. 3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных. Энергия магнитного поля. Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф =LI, причем при изменении тока на d I магнитный поток изменяется на dФ= L d I. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу d А=I dФ =LI d I. Тогда работа по созданию магнитного потока Ф будет равна Следовательно, энергия магнитного поля, связанного с контуром, Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля. Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим
где Sl = V — объем соленоида. Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
Электрический заряд. Электризация тел. Закон сохранения электрического заряда. Закон Кулона. Точечный заряд. Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы. Все тела в природе способны электризоваться, т. е. приобретать электрический заряд. Электрический заряд — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материальной точки, является физической абстракцией. Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними: где F12 — сила, действующая на заряд Q1 со стороны заряда Q2, r12 — радиус-вектор, соединяющий заряд Q2 с зарядом Q1, r = |r12|. На заряд Q2 со стороны заряда Q1 действует сила F21 = –F12.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.006 с.) |

 где k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид
где k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид 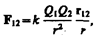
 напряженность поля точечного заряда в вакууме
напряженность поля точечного заряда в вакууме



 Первое правило Кирхгофа вытекает из закона сохранения электрического заряда.
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда.




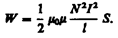 Так как I=Bl/ (m 0 mN) (см. (119.2)) и В=m 0 mH (см. (109.3)), то
Так как I=Bl/ (m 0 mN) (см. (119.2)) и В=m 0 mH (см. (109.3)), то 
 Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам (см. § 132).
Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам (см. § 132).


