
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельный колебательный контурСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
5.1 Цель работы: изучение характеристик простого и сложного параллельных колебательных контуров.
5.2 Оборудование и материалы: электрический стенд для исследования простого и сложного колебательных контуров, генератор гармонических колебаний, милливольтметр В3-33. Принципиальная схема стенда приведена на рисунке 5.1. С помощью проводников между гнездами 2, 1 (вход) и гнездами 9, 10 или 10, 13 (выход) стенда обеспечивается включение цепи, состоящей из резистора R1 или R2, конденсаторов С1, С2 и катушки индуктивности L. Упрощенные принципиальные схемы стенда приведены на рисунке 5.2.
Рисунок 5.1 – Принципиальная электрическая схема стенда
Рисунок 5.2 – Упрощенные принципиальные схемы стенда (контур простой)
Резисторы R1, R2 с различными сопротивлениями предназначены для увеличения внутреннего сопротивления источника гармонического напряжения. С помощью резисторов изучается влияние внутреннего сопротивления источника на резонансные характеристики контура. Простой параллельный колебательный контур образуется последовательно соединенными конденсаторами С1 и С2 в одной ветви и катушкой индуктивности L, включенной между гнездами 8, 14, в другой ветви. Гнезда 5 и 6 (7 и 8), 11 и 12 соединяются электрическими проводниками. Выходное напряжение снимается с гнезд 9, 10. Сложный параллельный колебательный контур (рисунок 5.3) образуется последовательно соединенными катушкой индуктивности L, подключаемой к гнездам 11, 12, и конденсатором С1 в одной ветви и конденсатором С2 в другой. Гнезда 5 и 15 (7 и 15), 8 и 14 соединяются между собой электрическими проводниками. Выходное напряжение снимается в этом случае с гнезд 10, 13.
Рисунок 5.3 – Упрощённые принципиальные схемы стенда (контур сложный)
В качестве источника гармонического напряжения используется низкочастотный генератор. Напряжение на входе стенда (гнезда 1, 2) устанавливается и контролируется по измерительному прибору генератора. Выходное напряжение стенда (напряжение на колебательном контуре) измеряется милливольтметром, который подключается к гнездам «Вых» стенда (гнезда 9, 10 или 10, 13).
Сведения из теории В усилительных каскадах радиоприемников широко используются избирательные цепи, состоящие из параллельно соединенных катушки индуктивности и конденсатора, называемые простым колебательным контуром. Цепи с двумя катушками индуктивности или с двумя конденсаторами, включёнными в разных ветвях, называются сложными контурами.
Три варианта схем параллельного колебательного контура изображены на рисунке 5.4.
Рисунок 5.4 – Три варианта схем параллельного колебательного контура
Схема, обобщающая три разновидности параллельного контура, показана на рисунке 5.5.
Рисунок 5.5 – Обобщенная схема параллельного контура
Зависимость комплексного сопротивления
где Сопротивление потерь В простом колебательном контуре обычно величиной
Реактивная проводимость В определяется выражением:
Режим работы параллельного колебательного контура, при котором его реактивная проводимость (реактивное сопротивление) равна нулю, называется резонансом токов. Условие резонанса токов имеет вид:
Резонансная частота контура
На резонансной частоте сопротивление катушки индуктивности и конденсатора равны по величине и противоположны по знаку. Модуль этих сопротивлений называется характеристическим сопротивлением контура
Отношение характеристического сопротивления
При резонансе ток контура превосходит ток неразветвленной части цепи в Q раз, поэтому явление резонанса в параллельном контуре и называют резонансом токов. Комплексное сопротивление
где На резонансной частоте
Модуль выражения (5.6)
называют амплитудно-частотной характеристикой контура, а аргумент этого выражения
Рисунок 5.6 – Амплитудно-частотная и фазо-частотная характеристики простого контура Полосой пропускания контура Полосы пропускания параллельного контура можно определить по формуле:
Если источник сигнала с внутренним сопротивлением R i представить в виде эквивалентного генератора тока (рисунок 5.7), то эквивалентное сопротивление этой схемы будет равно параллельному соединению сопротивлений R i и
Рисунок 5.7 – Схема параллельного контура с учетом внутреннего сопротивления генератора
Добротность эквивалентного контура будет определяться выражением:
На рисунке 5.8 приведено несколько зависимостей
Рисунок 5.8 – Зависимость эквивалентного сопротивления от частоты при различных значениях R i
Из рассмотрения рисунка 5.8 видно, что с уменьшением R i уменьшается резонансное сопротивление
Физический смысл уменьшения добротности заключается в том, что доля энергии, переходящая в тепло, увеличивается за счет нагревания сопротивления Ri. Применение параллельного колебательного контура целесообразно с точки зрения только в том случае, когда внутреннее сопротивление генератора достаточно велико (Ri >> Z 0). Однако следует учесть, что с увеличением внутреннего сопротивления генератора сама величина напряжения на контуре UК падает, так как
В отличие от простого параллельного колебательного контура сложный параллельный колебательный контур с неполным включением емкости (рисунок 5.3) характеризуется еще одним параметром – коэффициентом включения pc, равным:
Поскольку такой контур содержит в качестве одной из ветвей последовательный колебательный контур, в нем наблюдается как резонанс токов, так и резонанс напряжений. Частота резонанса
где Частота резонанса напряжения
Поскольку
Сопротивление контура
Напряжение Сопротивление контура
Напряжение Амплитудно-частотная характеристика контура с неполным включением емкости изображена на рисунке 5.9.
Рисунок 5.9 – Амплитудно-частотная характеристика контура с неполным включением емкости
Фазо-частотная характеристика этого же контура приведена на рисунке 5.10.
Рисунок 5.10 – Фазо-частотная характеристика контура с неполным включением емкости
Если ко входу контура подключается источник напряжения с внутренним сопротивлением
Подготовка к лабораторной работе 5.4.1 По заданным величинам индуктивности L =0,05 Гн и емкостей C 1=0,5 мкФ и С 2=0,1 мкФ определить резонансную частоту 5.4.2 Вычислить на резонансной частоте сопротивление контура Z о, эквивалентную добротность Q э и напряжение на простом контуре U к (рисунок 5.2а) сначала при внутреннем сопротивлении источника R 1 = 20 кОм, затем при внутреннем сопротивлении R 2 = 5,1 кОм. Для вычисления воспользоваться выражениями (5.7), (5.11), (5.13). Определить полосы пропускания контура, соответствующие сопротивлениям R 1 и R 2, воспользовавшись формулой (5.12). Добротность катушки индуктивности Q = 70. Потерями в конденсаторах C 1 и С 2 пренебречь. Действующее значение напряжения на входе стенда U = 1 В. 5.4.3 Вычислить сопротивление контура Z 0С, эквивалентную добротность Qэс, полосу пропускания и напряжение при резонансе токов в сложном контуре (рисунок 5.3а). Внутреннее сопротивление источника R 1=20 кОм, сопротивление индуктивности R =10 Ом. Напряжение на входе стенда 1 B. Для вычисления Z 0С воспользоваться выражением (5.19). Расчёт Q эс, U кc и D 5.4.4 Определить частоту резонанса напряжений в сложном контуре (рисунок 5.3а) по формуле (5.16). 5.4.5 Вычислить величины всех напряжений и токов в сложном контуре (рисунок 5.3а) на частоте, находящейся посередине между частотами резонанса напряжений и резонанса токов. Потерями в контуре пренебречь. Напряжение на входе стенда 1 В. Внутреннее сопротивление источника равно R 1=20 кОм. Расчет выполнить по формулам:
5.5 Порядок выполнения работы
5.5.1 Установить действующее значение напряжения на входе стенда IB. Собрать электрическую схему, изображённую на рисунке 5.2а. С помощью милливольтметра, подключённого к гнёздам 9, 10 стенда, определить резонансную частоту контура. 5.5.2 Найти граничные частоты
5.5.3 Снять зависимость напряжения на простом контуре от частоты. Действующее значение напряжения на входе стенда установить равным 1В. В крайних точках снятой зависимости напряжение на контуре должно составлять не более 0,1 от величины напряжения на нём при резонансе.
5.5.4 Собрать электрическую схему, представленную на рисунке 5.3б. Повторить п. 5.5.2. 5.5.5 Повторить п. 5.5.3 при внутреннем сопротивлении источника R2=5,1 кОм. 5.5.6 Собрать схему, изображённую на рисунке 5.3а. С помощью милливольтметра, подключённого к гнёздам 10, 13 стенда, определить частоту резонанса токов. 5.5.7 Найти граничные частоты 5.5.8 Определить частоту резонанса напряжений в сложном контуре. При резонансе напряжений напряжение на контуре имеет минимальное значение и составляет несколько милливольт. 5.5.9 Снять зависимость напряжения на сложном параллельном контуре от частоты. Действующее значение напряжения на входе стенда установить равным 1В. Частоту следует изменять в пределах ± 35 % относительно частот резонанса. 5.5.10 Собрать схему, изображённую на рисунке 5.3б. Повторить п. 5.5.9.
Обработка результатов 5.6.1 Построить зависимость напряжения на контуре от частоты по данным, полученным в пп. 5.5.3, 5.5.5, 5.5.9, 5.5.10 лабораторного задания. Все графики выполнить в одном масштабе. 5.6.2 Построить отдельно зависимость напряжения на сложном контуре в окрестностях резонанса напряжений, изменив по оси напряжений масштаб таким образом, чтобы был виден резонансный характер кривой. 5.6.3 Вычислить абсолютные и относительные погрешности измерений.
Контрольные вопросы 1. В чём состоит явление резонанса в параллельном колебательном контуре? 2. Как рассчитывается величина сопротивления параллельного контура при резонансе? 3. Как зависит эквивалентная добротность контура от внутреннего сопротивления источника? 4. Как изменится полоса пропускания простого контура, если его зашунтировать активным сопротивлением, равным резонансному сопротивлению контура? 5. Как изменится добротность, резонансная частота и эквивалентное резонансное сопротивление простого контура, если индуктивность и сопротивление потерь контура уменьшить, а емкость увеличить в два раза? 6. Написать аналитическое выражение для комплексного сопротивления параллельного контура. 7. Начертить фазовую характеристику параллельного контура при различных добротностях. 8. Изобразить эквивалентные схемы замещения параллельного контура на различных частотах. 9. Показать характер изменения полного сопротивления Z, активной составляющей R и реактивной составляющей X от частоты вблизи резонанса токов для последовательной схемы замещения простого параллельного контура. 10. Почему при подключении к источнику напряжения эквивалентная добротность сложного параллельного контура больше эквивалентной добротности простого параллельного контура? 11. Изобразить (качественно) векторную диаграмму всех напряжений и токов для сложного колебательного контура без потерь, имеющего две катушки индуктивности и конденсатор: − для частоты, лежащей ниже частоты резонанса токов;
− для частоты, совпадающей с частотой резонанса токов; − для частоты, лежащей между частотами резонанса токов и резонанса напряжений; − для частоты, совпадающей с частотой резонанса напряжений; − для частоты, лежащей выше частоты резонанса напряжений.
Рекомендуемая литература: [1, с. 175–187; 2, с. 131–140; 3, с. 130–140; 4, с. 268–272]
Лабораторная работа № 6 СВЯЗАННЫЕ КОНТУРЫ
6.1 Цель работы: изучение частотных характеристик связанных двухконтурных цепей. 6.2 Оборудования и материалы: электрический стенд для исследования частотных характеристик связанных двухконтурных цепей, генератор гармонических колебаний, милливольтметр В3-33. Принципиальная электрическая схема стенда приведена на рисунке 6.1. В работе предусмотрено изучение частотных характеристик двух типов связанных контуров. Система связанных контуров первого типа образована апериодическим и колебательным контурами (рисунок 6.2а). Контуры связаны между собой внутренней ёмкостной связью, которая осуществляется с помощью конденсатора С св общего для обоих контуров. В первый контур входят резистор R, конденсатор С 1. Во второй – конденсатор С 2, катушка индуктивности L 2 и конденсатор С 3. Выходными гнёздами стенда являются гнёзда 18, 19, подключенные к конденсатору большой ёмкости С 3, что позволяет уменьшить влияние измерительных приборов на характеристики контура. Система связанных контуров второго типа образована двумя колебательными контурами с одинаковыми параметрами (рисунок 5.2б). Как и в предыдущем случае, контуры связаны между собой ёмкостной связью, которая может изменяться путём подключения различных ёмкостей связи. Причём при изменении связи собственные резонансные частоты обоих контуров остаются неизменными. Конденсатор связи С св является общим для обоих контуров. В первый контур входят, кроме того, катушка индуктивности L 1 и конденсатор С 1. Во второй – конденсатор С 2, катушка индуктивности L 2 и конденсатор С 3. При использовании в качестве конденсатора связи С св конденсатора С св2 обеспечивается параметр (фактор) связи, равный 1; при использовании конденсатора С св1 параметр связи равен 0,5; при использовании конденсатора С св3 параметр связи равен 2.
Рисунок 6.1 – Принципиальная электрическая схема стенда для исследования связанных контуров
Рисунок 6.2 – Упрощённая принципиальная схема стенда а) один из связанных контуров апериодический; б) оба контура колебательные
Система связанных контуров с апериодическим контуром образуется путём соединения с помощью проводников гнёзд 3 и 8, 4 и 9, 12 и 13, 14 и 16, 15 и 17. Система связанных контуров с двумя колебательными контурами образуется путем соединения с помощью проводников гнёзд 5 и 6, 4 и 16, 15 и 17, 13 и 12 или 13 и 11, или 13 и 10. В качестве источника гармонического напряжения в работе используется низкочастотный генератор, который подключается ко входу стенда (гнёзда 1, 2). Напряжение на входе стенда устанавливается и контролируется по измерительному прибору генератора, на входе – по высокочастотному милливольтметру. Для уменьшения внутреннего сопротивления источника гармонического напряжения на входе стенда включен понижающий трансформатор.
Сведения из теории В радиотехнике в качестве избирательных цепей часто используются цепи, содержащие два или несколько влияющих друг на друга или связанных контура. Три варианта схем связанных контуров с различными типами связи (индуктивной, ёмкостной и трансформаторной) изображены на рисунке 6.3. Взаимное сопротивление, входящее в состав каждого из двух смежных контуров, называется сопротивлением связи. Контур, в который входит источник питания, называется первичным, а связанный с ним – вторичным. Для количественной оценки степени связи между контурами используют коэффициент связи, который определяется выражением:
где k 12, k 21 – коэффициенты передачи напряжения из первичного контура во вторичный и из вторичного в первичный соответственно; ½Хсв½ – абсолютная величина реактивного сопротивления связи между контурами; Х1, Х2 – реактивные сопротивления соответственно первичного и вторичного контуров. Для схемы на рисунке 6.3в
Рисунок 6.3 – Три варианта схем двух связанных контуров с различными типами связи (трансформаторной, индуктивной, ёмкостной)
Рисунок 6.4 – Т-образная схема замещения двух связанных контуров.
где
На рисунке 6.4 представлена обобщённая Т-образная схема замещения двух связанных контуров. Обозначим суммарное сопротивление, получаемое при обходе первичного контура
Если бы первичный контур был одиночный, то его входное сопротив-ление
и подставив в (6.5) вместо
где Аналогичные рассуждения справедливы и для вторичного контура. Таким образом, эквивалентные схемы замещения первичного и вторичного контуров будут иметь вид, представленный на рисунке 6.5.
Рисунок 6.5 – Эквивалентные схемы замещения первичного и вторичного контуров
Величина вносимых сопротивлений зависит только от сопротивления связи и параметров контура, из которого вносится сопротивление. Поэтому вносимые сопротивления характеризуют влияние контуров друг на друга. При настройке системы связанных контуров добиваются получения максимального тока I 2 во втором контуре при заданной частоте f и неизвестной э.д.с. Е источника питания путём подбора оптимальных значений реактивных параметров системы Х 1, Х 2 и Х св. Получить максимальное значение тока I 2 можно двумя способами: − путём подбора реактивного сопротивления первичного контура Х 1 при постоянных значениях параметров схемы Х св и Х 2, т.е.: Х 1 = var; X cв = const; Х 2 = const; − путём регулировки реактивного сопротивления Х 2, при неизменных значениях величин Х св и Х 1, т.е.: Х 2 = var; Х св = const; Х 1 = const. Режим работы системы, соответствующий первому способу настройки, называется первым частным резонансом. Условие первого частного резонанса имеет следующий вид:
Достигаемое при этом значение вторичного тока:
Режим работы системы, соответствующий второму способу настройки, называется вторым частным резонансом. Его условие:
при этом амплитуда вторичного тока:
Режим работы системы, когда каждый контур в отдельности настроен в резонанс (т.е. Х 11= Х 22=0), а сопротивление связи имеет произвольное постоянное значение (Х св=const), называется основным или индивидуальным резонансом. При настройке системы на индивидуальный резонанс автоматически выполняются условия настройки и на первый, и на второй частные резонансы, так как в этом случае Х вн1 = Х вн2 =0. Значение амплитуды вторичного тока при основном резонансе определяется выражением:
причём значение амплитуды тока I 2Р гораздо больше, чем получаемое при частных резонансах. Режим работы системы, при котором выполнено условие одного из частных резонансов и подобрана оптимальная связь между контурами Х св = Х св.опт, называется сложным резонансом. Значение вторичного тока при сложном резонансе достигает максимально возможной величины I 2mm. При условии первого частного резонанса и
значение вторичного тока достигает величины, равной:
Аналогичное значение тока I 2mm получается при втором частном резонансе и
Режим работы системы, при котором производится настройка на индивидуальный резонанс (основной резонанс) Х 11= Х 22=0 и подбирается оптимальное значение сопротивления связи Х св.опт = Амплитуда тока I2 при этом достигает той же величины I 2mm, что и при сложном резонансе, но для этого требуется значительно меньшее сопротивление связи Форма амплитудно-частной характеристики связанных контуров зависит лишь от коэффициента связи k и добротностей контуров Q 1 и Q 2:
где Для значений k < k КР, где
резонансная кривая имеет одногорбый характер, а максимальное значение тока вторичного контура достигается на частоте f = f 02 и определяется выражением:
Как видно из выражения (6.14), оно меньше максимально возможного значения I 2mm. При k = k КР кривая по-прежнему имеет одногорбый характер, но ток возрастает и достигает значения:
Если же k > k КР, то амплитудно-частотная характеристика становится двугорбой: ток достигает своего максимального значения на медленной f ом и быстрой f об частотах связи, а на частоте f 02 наблюдается впадина. Значения частот f ом и f об определяются выражениями:
Чем больше значение k, тем сильнее отличаются f ом и f об друг от друга и от f o2. Если k >> k КР, то выражения для f ом и f об приобретают вид:
Если первичный и вторичный контуры идентичны Q 1= Q 2= Q и f o1= f o2= f o, то значение критического коэффициента связи определится выражением:
С использованием принятых в теории связанных колебательных контуров понятий обобщённой расстройки
На рисунке 6.6 приведены частотные характеристики двух связанных контуров при различных параметрах связи А, из которых можно сделать следующие выводы: − при А ≤ 1 частотная характеристика имеет единственный максимум при x=0 (f = f 0), причём, ток вторичного контура не достигает своего максимально возможного значения I 2 mm; − при А > 1 получаются два максимума при − при А = 1 (связь равна критической) резонансная кривая остаётся одногорбой и имеет уплощённую верхнюю часть. Физически существование максимумов тока вторичного контура на медленной f ом и быстрой f об частотах связи объясняется тем, что на них реактивная составляющая собственного сопротивления каждого из контуров компенсируется реактивной составляющей вносимого сопротивления. Полосой пропускания системы связанных контуров называют область частот, на границах которой ток I 2 составляет не менее При А = 1 полоса пропускания связанных колебательных контуров в При А > 2,41 значение I 2 на резонансной частоте (x=0) упадёт ниже 0,707· I 2mm, поэтому полоса пропускания связанных контуров распадётся на два участка.
Подготовка к лабораторной работе 6.4.1 Найти частоту f 2 второго частного резонанса в системе связанных контуров (рисунок 6.2а). Сопротивление первого контура R =1 кОм, ёмкость первого и второго контуров С 1= С 2=33 нФ, индуктивность L 2=0,05 Гн, С СВ1=1,33 мкФ. Расчёт выполнять по формуле:
где
Рисунок 6.6 – Частотные характеристики двух связанных контуров
6.4.2 Используя результаты п. 6.4.1, определить полосу пропускания системы связанных контуров. Собственная добротность второго контура Q2 = 20, параметр А = 0,5. Расчёт провести по формуле:
6.4.3 Для системы связанных контуров (рисунок 6.2б) вычислить значения ёмкости связи С св при параметре связи А=0,5;1 и 2, используя выражение:
Добротность контуров Q 1= Q 2= Q =20, С 1=33 нФ. 6.4.4 Вычислить медленную f ом и быструю f об частоты связи при А=2, используя формулы:
где Q = 20 и
Порядок выполнения работы 6.5.1 Определить частоту второго частотного резонанса в системе связанных контуров апериодического и колебательного (рисунок 6.2а). А=0,5 (конденсатор С св=1,33 мкФ). Напряжение на входе стенда U вх=0,1 В. 6.5.2 Снять резонансную кривую и определить полосу пропускания системы связанных контуров (рисунок 6.2а). 6.5.3 В последующих пунктах производится исследование системы связанных контуров, состоящей из двух одинаковых колебательных контуров (рисунок 6.2б). Действующее значение напряжения на входе стенда Uвх = 0,1 В. 6.5.4 Снять резонансную кривую системы связанных контуров при параметре связи А=0,5 (Ссв = 1,33 мкФ). 6.5.5 Снять резонансную кривую при А=1 (Ссв = 0,67 мкФ). 6.5.6 Снять резонансную кривую при А=2 (Ссв = 0,33 мкФ).
Обработка результатов 6.6.1 По результатам пп. 6.5.2; 6.5.4 построить на одном чертеже резонансные кривые апериодической системы связанных контуров. 6.6.2 По результатам пп. 6.5.4 – 6.5.6 построить на одном чертеже резонансные кривые колебательной системы связанных контуров. 6.6.3 По результатам пп. 6.6.1 – 6.6.2 определить полосы пропускания систем связанных контуров. Контрольные вопросы: 1. Какие бывают типы связи между контурами? 2. Какие бывают типы резонансов в системе двух связанных контуров? 3. Что такое взаимное сопротивление? 4. Начертить эквивалентные схемы замещения первого и второго связанных контуров. 5. Записать усло
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.25.181 (0.016 с.) |






 параллельного контура (рисунок 5.5) от частоты питающего его гармонического источника тока определяется выражением:
параллельного контура (рисунок 5.5) от частоты питающего его гармонического источника тока определяется выражением: (5.1)
(5.1) ,
,  – сопротивления потерь, характеризующие потери в катушке индуктивности и конденсаторе.
– сопротивления потерь, характеризующие потери в катушке индуктивности и конденсаторе. и
и 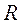 , его комплексную проводимость
, его комплексную проводимость 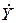 можно записать в виде:
можно записать в виде: ;
; .
. . (5.2)
. (5.2) определяется выражением:
определяется выражением: . (5.3)
. (5.3) . (5.4)
. (5.4)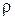 к сопротивлению R называется добротностью контура Q:
к сопротивлению R называется добротностью контура Q: . (5.5)
. (5.5) параллельного колебательного контура определяется выражением:
параллельного колебательного контура определяется выражением: (5.6)
(5.6) – обобщенная расстройка.
– обобщенная расстройка.
 сопротивление контура активно, максимально и равно:
сопротивление контура активно, максимально и равно: . (5.7)
. (5.7) (5.8)
(5.8) – фазо-частотной характеристикой контура. Эти характеристики изображены на рисунке 5.6.
– фазо-частотной характеристикой контура. Эти характеристики изображены на рисунке 5.6.
 называют область частот, на границах которой сопротивление контура меньше резонансного значения
называют область частот, на границах которой сопротивление контура меньше резонансного значения  в
в  раз. На границах полосы пропускания
раз. На границах полосы пропускания  =
=  1.
1. . (5.9)
. (5.9) :
: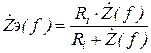 . (5.10)
. (5.10)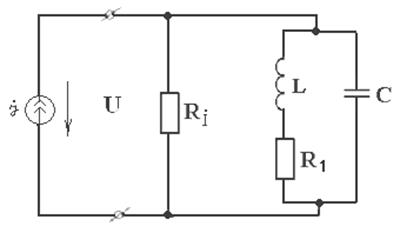
 . (5.11)
. (5.11) от частоты источника тока при различных значениях R i.
от частоты источника тока при различных значениях R i.
 и добротность
и добротность 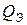 и увеличивается полоса пропускания
и увеличивается полоса пропускания . (5.12)
. (5.12)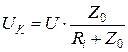 (5.13)
(5.13)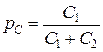 . (5.14)
. (5.14)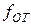 рассчитывается по формуле:
рассчитывается по формуле: , (5.15)
, (5.15) .
. определяется параметрами последовательного колебательного контура:
определяется параметрами последовательного колебательного контура: . (5.16)
. (5.16) <
<  , частота резонанса напряжений
, частота резонанса напряжений  на частоте резонанса токов определяется выражением:
на частоте резонанса токов определяется выражением: , (5.17)
, (5.17)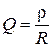 . (5.18)
. (5.18) на частоте
на частоте  носит активный характер, максимально и определяется выражением:
носит активный характер, максимально и определяется выражением: . (5.19)
. (5.19) на контуре на этой частоте также будет достигать максимального значения.
на контуре на этой частоте также будет достигать максимального значения. на частоте
на частоте  . (5.20)
. (5.20) на этой частоте также будет минимальным.
на этой частоте также будет минимальным.

 , то эквивалентная добротность контура
, то эквивалентная добротность контура  увеличивается, их величины рассчитываются по формулам (5.11) и (5.12) соответственно.
увеличивается, их величины рассчитываются по формулам (5.11) и (5.12) соответственно. простого параллельного колебательного контура (рисунок 5.2), используя выражение (5.3). Потерями в контуре пренебречь.
простого параллельного колебательного контура (рисунок 5.2), используя выражение (5.3). Потерями в контуре пренебречь. выполнить по формулам (5.11), (5.13), (5.12).
выполнить по формулам (5.11), (5.13), (5.12). ,
,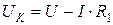 ,
,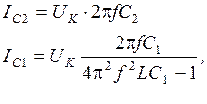


 и
и  полосы пропускания параллельного контура при внутреннем сопротивлении источника R 1=20 кОм и определить эквивалентную добротность контура, используя выражение:
полосы пропускания параллельного контура при внутреннем сопротивлении источника R 1=20 кОм и определить эквивалентную добротность контура, используя выражение: .
.

 , (6.1)
, (6.1) ,
,  ,
, 


 ,
, ,
,  . (6.2)
. (6.2) , а суммарное сопротивление при обходе вторичного контура –
, а суммарное сопротивление при обходе вторичного контура –  , то есть
, то есть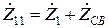 , (6.3)
, (6.3) . (6.4)
. (6.4) . Учитывая, что
. Учитывая, что , (6.5)
, (6.5) его значение из (6.4), получим для
его значение из (6.4), получим для  выражение:
выражение: , (6.6)
, (6.6) – называется вносимым сопротивлением.
– называется вносимым сопротивлением.
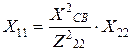 . (6.7)
. (6.7) . (6.8)
. (6.8) , (6.9)
, (6.9) . (6.10)
. (6.10)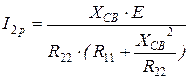 , (6.11)
, (6.11) ,
, . (6.12)
. (6.12) .
. , называется полным резонансом.
, называется полным резонансом. .
. ,
, .
. , (6.13)
, (6.13) . (6.14)
. (6.14) .
. ,
,  ;
; ,
,  .
. ,
,  .
. .
. и параметра связи
и параметра связи  выражение для тока вторичного контура запишется тогда в виде:
выражение для тока вторичного контура запишется тогда в виде: .
. и
и  и минимум при x=0; максимальное значение тока в «горбах» резонансных двугорбых характеристик равно I 2mm;
и минимум при x=0; максимальное значение тока в «горбах» резонансных двугорбых характеристик равно I 2mm; от своего максимального значения I 2mm.
от своего максимального значения I 2mm. раз больше, чем у одиночного контура. При очень слабой связи (А<1) полоса пропускания составляет приблизительно 0,64 от полосы пропускания одиночного контура.
раз больше, чем у одиночного контура. При очень слабой связи (А<1) полоса пропускания составляет приблизительно 0,64 от полосы пропускания одиночного контура. ,
, ,
,  ,
, ,
, 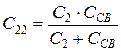 .
.
 .
. .
. ,
, .
.



