Резонанс в последовательном контуре.

Рассмотрим простейший колебательный контур (рис. 2.23).

Комплексное сопротивление цепи

. (2.35)

Рис. 2.23. RLC колебательный контур

Резонанс наступает при .

Напряжения на индуктивности и емкости при этом оказываются равными друг другу по величине (U_L = X_LI = U_C = X_CI) и скомпенсированными друг с другом. Приложенное напряжение падает только на активном сопротивлении. Полное сопротивление Z при X = 0 будет равно и при заданном напряжении ток I достигает максимального значения I_max.

Условие равенства ωL = 1/ωC показывает, что в общем случае резонансных условий можно достичь, изменяя или параметры цепи L и C или частоту питания ω. Угловая частота

(2.36)

называется резонансной угловой частотой.

Сопротивление

(2.37)

называется характеристическим или волновым.

В том случае, когда активное сопротивление цепи много меньше волнового, напряжения на индуктивности и емкости значительно превосходят по величине напряжение на зажимах цепи. Количественно различие этих величин принято определять с помощью так называемой добротности контура Q:

. (2.38)

Величина, обратная добротности, называется затуханием

. (2.39)

Это наименование связано с тем, что при отключении колебательного контура от источника, когда контур замыкается накоротко, колебательный процесс затухает тем интенсивнее, чем больше величина d.

В режиме резонанса суммарная энергия электрического и магнитного полей остается постоянной. Действительно, если ток в контуре определяется величиной i = I_msin ω₀t, то напряжение на емкости будет

.

Энергия полей будет определяться выражениями

,

.

Их сумма

.

Учитывая, что или , будем иметь .

Кроме факта постоянства суммы энергий электрического и магнитного полей, произведенные выкладки показывают и существующий непрерывный обмен энергиями этих полей. Энергия, поступающая от источника питания, преобразуется в тепло активным сопротивлением. Поэтому вся цепь эквивалентна активному сопротивлению.

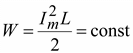Частотные характеристики последовательного колебательного контура

 

Под частотными характеристиками цепи понимают зависимости от частоты тех величин, которые характеризуют ее свойства (рис. 2.24). В рассматриваемом случае такими величинами оказываются индуктивное, емкостное и реактивное сопротивления, напряжения на отдельных участках цепи, а также сдвиг фаз между током и приложенным напряжением. Зависимость тока и напряжений от частоты называют резонансными кривыми (рис. 2.25). Рис. 2.24. Частотные характеристики Рис. 2.25. Резонансные кривые Характер кривых определяется их аналитическими выражениями: XL = ωL, XC = 1/ωC, X = XL – XC = ωL – 1/ωC, , , , . Если учесть, что реальная катушка индуктивности обладает активным сопротивлением провода, а конденсатор - сопротивлением утечки, то при исследовании UL = f1(ω) и UC = f2(ω) оказывается, что максимум UL наступает при частоте , а максимум UC наступает при . Следовательно, расхождение частот ωL и ωC будет тем больше, чем больше затухание d. Резонансная кривая тока показывает избирательные свойства последовательного контура. Он обладает наименьшим сопротивлением при частотах, близких к резонансной; при отклонении частоты в ту или другую сторону сопротивление контура растет. Выражение тока в цепи можно привести к виду: , которое показывает, что с возрастанием добротности кривая становится более острой; цепь более «избирательна» в своем поведении к резонансной частоте (рис. 2.26). Рис. 2.26. Избирательность контура Вводится понятие полосы пропускания контура следующим образом: Отсюда где 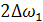– полоса пропускания контура.   Рис. 2.2. Частотная характеристика последовательного контура   Часто интересует коэффициент передачи цепи, изображенной на рис. 2.1. Итак (2.6) Важную роль играет фаза коэффициента – это его аргумент, поэтому . На рис. 2.3 изображена зависимость фазы от частоты. Обратим внимание на то, что в пределах полосы пропускания фаза линейно зависит от частоты. 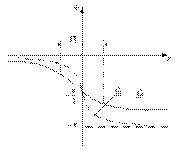Рис. 2.3. Фазовая характеристика коэффициента передачи   Резонанс в параллельном контуре   Резонанс возникает при условии равенства нулю реактивной проводимости B = BL – BC = 0 или 1/ω0L = ω0C. Взаимная компенсация индуктивной и емкостной проводимостей возникает при условии , т.е. при том же условии, при котором имеет место резонанс в последовательном контуре (при резонансе напряжений). В режиме резонанса токов полная проводимость достигает своего минимального значения, равного G, а полное сопротивление цепи при этом, в отличие от резонанса напряжений, имеет максимальное значение. Поэтому ток в неразветвленной части цепи имеет минимальное значение. Соответствующая векторная диаграмма показана на рис. 2.27. Так как векторы IL и IC направлены противоположно друг другу и равны по величине, то на векторной диаграмме вектор тока I в неразветвленной части цепи равен по величине и направлению вектору IR = GU, изображающему ток в ветви с активным сопротивлением. Рис. 2.27. Векторная диаграмма при резонансе токов При этом может оказаться, что токи в индуктивности и емкости будут превосходить ток в неразветвленной части цепи. Такое положение может возникать, когда G < 1/ω0L = ω0C. Поскольку , то это условие приводит к следующему . Величину 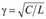называют волновой проводимостью цепи. Отношение активной проводимости G к волновой называют затуханием цепи . Затухание также показывает во сколько раз ток в неразветвленной части цепи меньше (или больше) тока в ветви с емкостью или индуктивностью . Умножив числитель и знаменатель на напряжение U, получим . Величина, обратная затуханию цепи, называется добротностью Q. С энергетической точки зрения процессы при параллельном резонансе аналогичны процессам в цепи с последовательным резонансом. Энергия магнитного поля катушки в течение четверти периода тока переходит в энергию электрического поля конденсатора, и в последующую четверть периода возвращается обратно из конденсатора в катушку. Обмен энергиями между полями цепи и источником питания не происходит. Явление резонанса токов имеет важное значение в электроэнергетике. Так как основными потребителями электроэнергии являются двигатели, которые представляют собой активно-индуктивную нагрузку, то установка потребителей емкостной мощности вблизи приемников позволяет снизить токи, протекающие по ЛЭП, и тем самым уменьшить потери электроэнергии.