

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Топографическая векторная диаграмма.
Рассматривается график распределения потенциала для простейшей цепи постоянного тока. В случае цепи гармонического тока аналогично строится другой график, который называется потенциальной или топографической диаграммой напряжений. Эта диаграмма представляет собой векторную диаграмму, на которой отложены комплексные потенциалы отдельных точек заданной цепи по отношению к одной точке, потенциал которой принят за нуль. Таким образом, порядок расположения векторов падения напряжения на диаграмме строго соответствует порядку расположения элементов цепи на схеме. Конец вектора напряжения на каждом последующем элементе примыкает к началу вектора напряжения предыдущего элемента. При таком построении векторной диаграммы напряжений каждой точке электрической цепи соответствует определенная точка на потенциальной диаграмме.
Потенциальная диаграмма позволяет весьма просто находить напряжения между любыми точками цепи: действующее значение и фаза искомого напряжения определяются прямой, соединяющей соответствующие точки потенциальной диаграммы.
На рисунке 3.11 изображена схема неразветвленной электрической цепи и для нее построена потенциальная диаграмма напряжений. Направления векторов напряжений на потенциальной диаграмме увязаны с произвольно выбранным направлением вектора тока I.
Обход схемы ведется навстречу положительному направлению тока 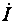 . В соответствии с порядком расположения в схеме элементов С, R2, L, R1 на диаграмме изображены векторы напряжений: . В соответствии с порядком расположения в схеме элементов С, R2, L, R1 на диаграмме изображены векторы напряжений:
 ; ;  ; ;
 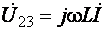 ; ;  . .
Начала и концы векторов (рисунок 3.11, б) пронумерованы в соответствии с нумерацией точек, принятой на схеме (рисунок 3.11, а).
А  
Б
Рисунок 3.11 Схема (а) и потенциальная диаграмма (б)
Напряжение между какими-либо двумя точками схемы, например, напряжение на участке 2–4 схемы, взятое в положительном направлении тока 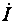 , определяется по потенциальной диаграмме вектором , определяется по потенциальной диаграмме вектором   , соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор , соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор  , представляющий разность напряжений (или потенциалов), направлен от конца вектора , представляющий разность напряжений (или потенциалов), направлен от конца вектора  к концу вектора к концу вектора 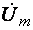 . Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему. . Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему.
Если при построении потенциальной диаграммы обход схемы совершался бы в положительном направлении тока 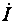 , то изменялась бы нумерация начала и конца каждого вектора напряжения на потенциальной диаграмме, что противоречило бы принятому правилу расстановки индексов при вычитании векторов. , то изменялась бы нумерация начала и конца каждого вектора напряжения на потенциальной диаграмме, что противоречило бы принятому правилу расстановки индексов при вычитании векторов.
Одноименные зажимы
При анализе цепей с взаимной индуктивностью возникает задача определить, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствие с этим какой знак (плюс или минус) необходимо использовать в выражениях (1), (2)
(1)  (2) (2)  . .
Если конструкции индуктивных катушек, в частности направления их намотки, известны, а направления токов заданы, то для выбора знака достаточно, воспользовавшись правилом буравчика (правоходового винта), определить направления магнитных потоков самоиндукции каждой из катушек. Например, применяя правило буравчика, устанавливаем, что у катушек, изображенных на рис. 3:
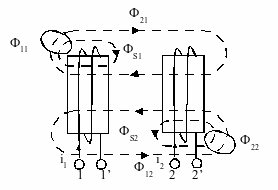 , направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы. , направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы.
При вычерчивании принципиальных электрических схем цепей с взаимной индуктивностью индуктивные катушки изображают с помощью условных графических обозначений, которые не отражают особенностей их конструкции. Для выяснения, является ли данное включение катушек согласным или встречным, вводят понятие одноимённых зажимов связанных индуктивных
Рис.3 катушек.
Одноименными зажимами двух связанных индуктивных катушек называется пара зажимов, выбранных таким образом при одинаковых относительно этих зажимов направлениях токов катушек магнитные потоки самоиндукции и взаимоиндукции в каждой из них суммируются. Одноименные зажимы индуктивных катушек помечают одинаковыми значками (буквами, точками, звездочками, треугольниками и т. п.), проставляемыми в непосредственной близости к соответствующим зажимам. Вторую пару одноименных зажимов катушек специально не обозначают (рис. 10.2).
Когда общим магнитным потоком связано не две, а большее количество индуктивностей, одноимённые зажимы каждой из пар обозначают с помощью различных значков.

Рис. 10.2. Условные графические обозначения связанных индуктивностей на эквивалентных схемах
Итак, если токи связанных индуктивностей одинаково ориентированы относительно одноименных зажимов, то такое включение является согласным и в выражениях (1):
 (1) (1)
следует использовать знак плюс, в противном случае, включение является встречным и необходимо использовать знак минус (величина М при этом считается положительной). Например, индуктивности L1 и L2 на рис. 10.2 включены согласно, а индуктивности L2 и L3, L1 и L3 - встречно.
Мощность в цепи синусоидального тока.


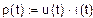


 Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение
Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение  и протекает ток и протекает ток  .
Мощность в активном сопротивлении .
Мощность в активном сопротивлении
 .
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь .
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
 . .
 Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
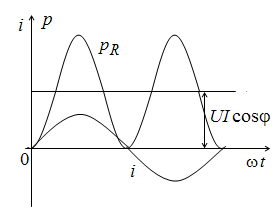 Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
 .
Но .
Но 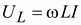 , следовательно, , следовательно,  . Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет. . Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
 Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости
Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости

 .
Кривые тока и мощности показаны на рис. 2.18. .
Кривые тока и мощности показаны на рис. 2.18.
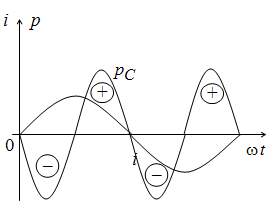 Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
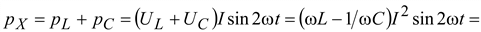
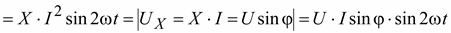 .
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При .
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При  , т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна , т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
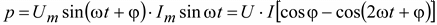 . (2.34)
Она состоит из двух слагающих: постоянной величины . (2.34)
Она состоит из двух слагающих: постоянной величины 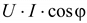 , равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность , равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность
 .
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности. .
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
 ; ;
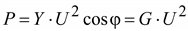 .
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности. .
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
 Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
 ; ;
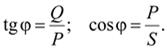
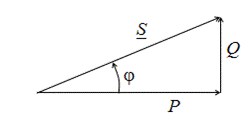 Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса
Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса  , сопряженного с комплексным током I , сопряженного с комплексным током I


  .
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S. .
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
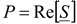 ; ;  ; ;
 ; ;
 . .

| |
Взаимная индуктивность. ЭДС взаимоиндукции. Коэффициент связи.
Под явлением взаимоиндукции понимается наведение ЭДС в электрической цепи при изменении потокосцепления взаимной индукции, обусловленного током в другой электрической цепи.
Цепи, в которых наводится ЭДС взаимной индукции называются индуктивно-связанными цепями.
M[Гн] – взаимная индуктивность – это отношение потокосцепления в
одной электрической цепи к току в другой электрической цепи.
(ω1*ФМ2)/ i2=M12 М12=М21 (катушка 1 влияет на 2, как и 2 на 1)
(ω2*ФМ1)/ i1=M21
ВЗАИМНАЯ ИНДУКТИВНОСТЬ, коэффициент взаимной индуктивности – величина, характеризующая отношение потокосцепления одной цепи (катушки) к току другой цепи (катушки), возбуждающему это потокосцепление. В Международной системе единиц (СИ) измеряется в генри (Г). Взаимная индуктивность зависит от числа витков катушек, их размеров и формы, взаимного расположения и магнитной проницаемости среды. Взаимная индуктивность двух катушек связана с их индуктивностью L1 и L2 следующим соотношением:
М = M 1-2 = М 2-1 = К / L 1L 2,
где К – коэффициент связи катушек, характеризующий степень их индуктивной связи; М – взаимная индуктивность, Г.
Коэффициент связи зависит от расположения катушек: при большем расстоянии между ними он уменьшается, при меньшем – увеличивается.
| 32 Условие передачи максимальной мощности от источника к приёмнику.
 ; то же для Zn ; то же для Zn 
 Первое условие:
Первое условие:  Тогда получим:
Тогда получим:
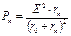


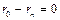 Получили второе условие:
Получили второе условие:  Максимальная мощность, которая выделится на нагрузке:
Максимальная мощность, которая выделится на нагрузке:
 Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
 или
или  и и  .
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна .
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна  .
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае .
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае 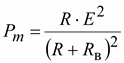 . .
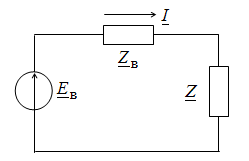 Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника  .
При этом условии .
При этом условии  .КПД в этом случае будет равно .КПД в этом случае будет равно
 . энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД. . энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД.
|
|



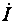 . В соответствии с порядком расположения в схеме элементов С, R2, L, R1 на диаграмме изображены векторы напряжений:
. В соответствии с порядком расположения в схеме элементов С, R2, L, R1 на диаграмме изображены векторы напряжений: ;
; 
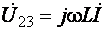 ;
;  .
.


 , соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор
, соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор  , представляющий разность напряжений (или потенциалов), направлен от конца вектора
, представляющий разность напряжений (или потенциалов), направлен от конца вектора  к концу вектора
к концу вектора 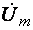 . Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему.
. Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему. (2)
(2)  .
. , направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы.
, направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы.
 (1)
(1)

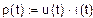


 Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение
Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение  и протекает ток
и протекает ток  .
Мощность в активном сопротивлении
.
Мощность в активном сопротивлении
 .
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
.
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
 .
.
 Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
 Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
 .
Но
.
Но 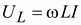 , следовательно,
, следовательно,  . Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
. Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
 Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости
Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости

 .
Кривые тока и мощности показаны на рис. 2.18.
.
Кривые тока и мощности показаны на рис. 2.18.
 Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
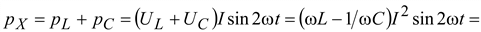
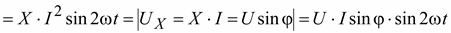 .
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При
.
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При  , т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
, т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
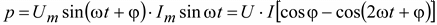 . (2.34)
Она состоит из двух слагающих: постоянной величины
. (2.34)
Она состоит из двух слагающих: постоянной величины 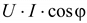 , равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность
, равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность
 .
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
.
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
 ;
;
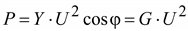 .
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
.
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
 Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
 ;
;
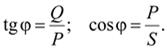
 Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса
Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса  , сопряженного с комплексным током I
, сопряженного с комплексным током I



 .
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
.
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
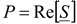 ;
;  ;
;
 ;
;
 .
.

 ; то же для Zn
; то же для Zn 
 Первое условие:
Первое условие:  Тогда получим:
Тогда получим:
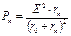


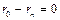 Получили второе условие:
Получили второе условие:  Максимальная мощность, которая выделится на нагрузке:
Максимальная мощность, которая выделится на нагрузке:
 Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
 или
или  и
и  .
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна
.
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна  .
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае
.
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае 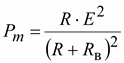 .
.
 Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника
Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника  .
При этом условии
.
При этом условии  .КПД в этом случае будет равно
.КПД в этом случае будет равно
 . энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД.
. энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД.



