
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим участок электрической цепи (рис. 16)
Рис. 16.
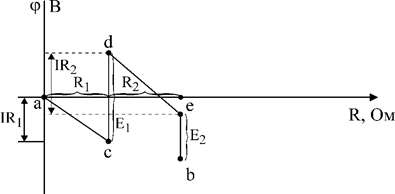
Участок ветви, содержащий один или несколько источников энергии, является активным. Положительные направления тока и напряжения указаны стрелкой. Определим потенциалы точек c, d, e, b, предположив, что известен потенциал точки a-ja. Для правильного выбора знаков следует помнить, что: 1) ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е. потенциал падает по направлению тока. 2) э.д.с., направленная от точки «с» к точке «d», повышает потенциал последней на величину E. 3) напряжение U=Uac положительно, когда потенциал точки а выше, чем потенциал точки с. При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она ставится в направлении от точки высшего потенциала к точке низшего потенциала. На рис. 16 ток протекает от точки «а» к точке «с», значит потенциал jс будет меньше ja на величину падения напряжения на сопротивлении R1, которое по закону Ома равно IR1: jс = ja - IR1 На участке cd э.д.с. E1 действует в сторону повышения потенциала, следовательно: jd = jс + E1 = ja - IR1+ E1 Потенциал точки «e» меньше потенциала точки «d» на величину падения напряжения на сопротивлении R2: je = jd – IR2 = ja - IR1+ E1– IR2 На участке e в э.д.с. E2 действует таким образом, что потенциал точки «b» меньше потенциала точки «e» на величину E2: jb = je – E2 = ja - IR1+ E1– IR2 – E2 = ja – I(R1+R2) + E1-E2 (15) Чтобы наглядно оценить распределение потенциала вдоль участка цепи, полезно построить потенциальную диаграмму, которая представляет график изменения потенциала вдоль участка цепи или замкнутого контура. По оси абсцисс графика откладываются потенциалы точек, а по оси ординат – сопротивления отдельных участков цепи. Для участка цепи рис. 16 распределение потенциала построено на рис. 17.
Рис. 16. Потенциальная диаграмма участка цепи.
Потенциальная диаграмма рис. 16 построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал ja принят равным нулю. Точка цепи, потенциал которой условно принимается равным нулю, называется базисной. Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса. Обобщенный закон Ома. Закон Ома выражаемый формулой Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16). Из формулы 15 следует: ja -jb=I(R1+R2)- E1+E2 (16) На положительное напряжение на участке a – b Uab=ja -jb Следовательно, Uab= I(R1+R2)- E1+E2 (17)
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с. Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-». Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы. Пример № 1. Построения потенциальной диаграммы: Построить потенциальную диаграмму для одноконтурной схемы:
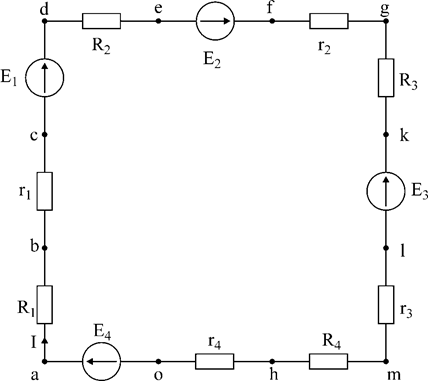
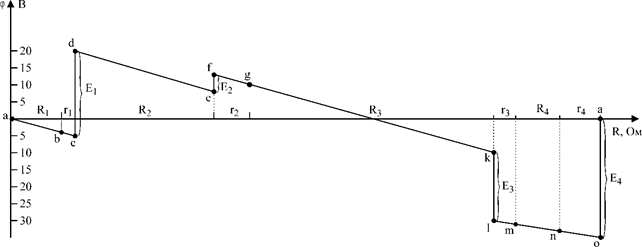
E1=25В; E2=5В; E3=20В; E4=35В, R1=8 Ом; R2=24 Ом; R3=40 Ом; R4=4 Ом, r1=2 Ом; r2=6 Ом; r3=2 Ом; r4=4 Ом. Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1- r4) за их пределы; обозначим точки контура.
Рис.2
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:
3. За базисную точку примем точку a. Найдем потенциалы остальных точек: jb = ja – IR1 = - 4В je = jd – IR2 = 8В jc = jb – Ir1 = - 5В jf = je + E2 = 13В jd = jc + E1 = 20В jq = jf – Ir2 = 10В
jk = jq – IR3 = - 10В jn = jm – IR4 = - 33В je = jk – E3 = - 30В jo = jn – Ir4 = - 35В jm = je – Ir3 = - 31В ja = jo + E4 = 0
4. В системе координат строим потенциальную диаграмму:
1. Метод контурных токов. Метод контурных токов.
Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно. Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Рис.28. Иллюстрация к методу контурных токов.
На рис.28 показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11 и I22. Токи в ветвях I1 и I2 равны контурным токам: I1=I11, I2=I22 Ток I3 равен сумме этих двух контурных токов: I3=I11+I22 По второму закону Кирхгофа для первого контура цепи: I1r1+I3r3=E1-E3 Или: I11r1+(I11+I22)r3=E1-E3; I11 (r1+r2)+I22r3=E1-E3 Обозначим r1+r2=r11 r3=r12; E1-E3 Тогда: I11r11+I2r12=E11 r11 – сумма всех сопротивлений, входящих в контур I, называется собственным сопротивлением контура. r12 – сопротивление ветви, общей для контура I и II; E11=E1-E2 – алгебраическая сумма всех э.д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура. E11 называется контурной э.д.с. Аналогично для второго контура рис.28. I11r21+I22r22=E22, где r21=r3; r22=r2+r3; E22=E2-E3 Уравнения, составленные по методу контурных токов, всегда записывают в виде системы. Для схемы рис.28:
В результате решения системы находят контурные токи, а затем токи ветвей. Если заданная электрическая цепь содержит n независимых контуров, то на основании второго закона Кирхгофа получается n контурных уравнений:
Собственные сопротивления rii входят в уравнения (29) со знаком «+», поскольку обход контура принимается совпадающим с положительным направлением контурного тока Iii. Общие сопротивления rik войдут в уравнения со знаком «-», когда токи Ii и Ik направлены в них встречно. Число уравнений, составляемых по методу контурных токов, определяется по формуле: Nур=Nb-Ny+1-Nи.т. где Nb – число ветвей электрической цепи; Ny – число узлов; Nи.т. – число идеальных источников тока.
Пример. Решим пример, используя метод контурных токов. (Для схемы рис.1 составить уравнения по законам Кирхгофа и определить неизвестные точки.) Дано: I1 = 20мA; I2 = 10мA R1 = 5kОм, R3 = 4kОм, R4 = 6kОм, R5 = 2kОм, R6 = 4kОм.
Цепь содержит три контура, через которые протекают контурные токи. При наличии источников тока надо так направлять контурные токи, чтобы они протекали через данные источники. Но через один источник тока не может протекать два контурных тока. На рис.1 обозначены положительные направления контурных токов. Очевидно, что I11=J1; I22=-J2 Контурный ток I33 – неизвестен, для него составляем уравнение: I33 (R3+R4+R5+R6)-I11 (R3+R4)+I22 (R5+R3)=0 В правой части уравнения стоит «0», т.к. отсутствует контурная э.д.с. В результате решения определяем I33=16,25 мА Итак: I1=I11=20мА; I3=I11-I22-I33=20-(-10)-16,25=13,75мА. I4=-I11+I33=-20+16,25=-3,75мА; I5=I22+I33=-10+16,25=6,25мА; I6=I33=16,25мА. 4. Применение законов Кирхгофа для расчета электрических цепей. 1 закон: алгебраическая сумма токов в узле равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
2 закон: алгебраическая сумма падений напряжений в замкнутом контуре равна алгебраической сумме ЭДС этого контура.
8. Метод наложения. Входные и взаимные проводимости и сопротивления. Метод наложения основан на принципе наложения: ток в любой ветви электрической цепи от действия нескольких источников равен алгебраической сумме токов от действия каждого источника в отдельности. Входные и взаимные проводимости. Решение системы уравнений по законам Кирхгофа записывается в виде
Где коэффициенты g11,g22… называются входными проводимостями, а g12, g13… наз-ся взаимными проводимостями. Отношение контурного тока к ЭДС, действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью. Отношение контурного тока к ЭДС, действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (взаимной) проводимостью. Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других независимых источников называется входным сопротивлением эл-кой цепи. Отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (взаимным) сопротивлением узлов.
8. Метод узловых потенциалов (напряжений). Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах эл-кой цепи относительно базисного узла. Эти разности потенциалов называются узловыми напряжениями. Узловое напряжение- это напряжение в данном узле относительно базисного. Напряжение на какой-либо ветви равно разности узловых напряжений; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Т.о., зная узловые напряжения в электрической цепи, можно найти токи в ветвях. Если принять потенциал базисного узла равным нулю, то напряжение между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов. Собственная проводимость равняется сумме проводимостей ветвей сходящихся в данном узле. Величина положительная. 9.Применение метода узловых потенциалов при наличии в цепи идеальных источников эдс. За базисный принимается один из узлов между которыми находится идеальный источник ЭДС. Дано: Найти токи МУН. Nур =1;
-
В ветви с идеальным источником ток находится по первому закону Кирхгофа:
Дано: Найти токи МУН. Nур =1;
11)Метод преобразования Суть метода преобразований состоит в упрощении цепи и, как следствие, ее расчета. Последовательное соединение: 1)Преобразуем схему к простой (склеиваем все r и Е) 2)Треугольники преобразуем в звёзды 3)Находим ток в ветви 4)Раскрываем ветвь и считаем всё по току который нашли
Ток протекает везде одинаковый. Напряжение равно сумме всех напряжений. При параллельном соединении напряжение везде одинаковое. G0=1/R1 [см] – проводимость величина обратная сопротивлению.(сименс)
12) Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.

13)Эквивалентные преобразования активных соединений звездой и треугольником. Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.
Преобразуем ЭДС в источник тока по формулам I=E/rвн, g=1/rвн
14)Метод основан на методе наложения и используется в том случае, если схема содержит один источник. В этом методе произвольно задается ток самой дальней ветви от источника. По закону Ома и законам Кирхгофа определяют расчетные значения ЭДС источника. Вычисляя отношение расчетного значения ЭДС к заданному значению, получают коэффициент пропорциональности: 15)Баланс мощностей в цепи постоянного тока. Из закона сохранения энергии следует, что вся мощность поступающая в цепь от источников энергии в любой момент времени равна всей мощности потребляемой приемниками данной цепи.
Т.к. ток входит в выражение в квадрате, то независимо от его направления мощность потребителя всегда положительна. Мощность источника бывает как положительной так и отрицательной. РЕ=IE, где I – ток ветви с источником:
Мощность источника тока определяется по формуле: PI=IU, где I- значение тока источника, U–напряжение на его зажимах. Если ЭДС и ток в ветви в которой он находится совпадают по направлению, то мощность источника ЭДС входит в выражение баланса мощностей со знаком «+», если не совпадает то «-». Если ток Iи напряжение Uдействуют так, как показано на рисунке, то мощность в источнике тока положительная в противном случае отрицательная.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.201 (0.007 с.) |


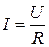 , определяет зависимость между током и напряжением на пассивном участке электрической цепи.
, определяет зависимость между током и напряжением на пассивном участке электрической цепи. (18)
(18)
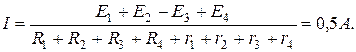


 (29)
(29) Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.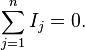
 .. 2 закон не записывается для контуров содержащих источники тока. Напряжение и ЭДС совпадающие с направлением обхода контура записываем со знаком (+), несовпадающие со знаком (-)
.. 2 закон не записывается для контуров содержащих источники тока. Напряжение и ЭДС совпадающие с направлением обхода контура записываем со знаком (+), несовпадающие со знаком (-) 
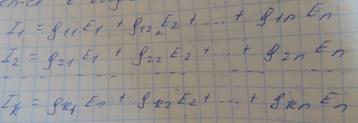


 =
=  =
= 
 -?
-? =
= 
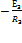
 ;
; ;
;

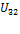 =-
=- 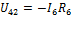 .
.



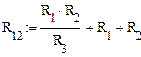





 .
.
 – мощность потребителей которыми в цепи постоянного тока являются резисторы.
– мощность потребителей которыми в цепи постоянного тока являются резисторы.


