
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность электрического поля и потенциалСодержание книги
Поиск на нашем сайте
где П — потенциальная энергия точечного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю). Сила, действующая на точечный заряд q, находящийся в электрическом поле, и потенциальная энергия этого заряда
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей),
где E i, ji— напряженность и потенциал в данной точке поля, создаваемого i-м зарядом. Напряженность и потенциал поля, создаваемого точечным зарядом q на расстоянии r
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой (с зарядом q) радиусом R на расстоянии r от центра сферы: a) E=0 б) в) Линейная плотность заряда
Поверхностная плотность заряда
Напряженность и потенциал поля, создаваемого системой распределенных зарядов, находят, разбивая систему на точечные заряды и используя принцип суперпозиции электрических полей (т.е. проводя интегрирование). Для расчета электростатических полей сложных заряженных объектов используется также теорема Гаусса:
где D =eeo E – электрическое смещение, S – замкнутая поверхность, окружающая заряды q i, Напряженность поля, создаваемого бесконечной равномерно заряженной прямой линией или бесконечно длинным цилиндром
где r — расстояние от нити или оси цилиндра до точки, в которой определяется напряженность поля. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
Связь потенциала с напряженностью: а) б) E = (φ 1 – φ 2 )/d в случае однородного поля; в) Электрический момент диполя
где q — заряд, 1 — плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами). Момент силы, действующей на диполь во внешнем электрическом поле
Потенциальная энергия диполя во внешнем электрическом поле
где a– угол между р и Е. Работа сил поля по перемещению заряда q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2 A 12 = q (φ1 – φ2). Электроемкость C = q/ jили C = q/U, где j — потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U — разность потенциалов пластин конденсатора. Электроемкость плоского конденсатора
где S — площадь пластины (одной) конденсатора; d — расстояние между пластинами. Электроемкость батареи N конденсаторов: а) б) Энергия заряженного конденсатора:
Сила постоянного тока
где q — заряд, прошедший через поперечное сечение проводника за время t.
Плотность тока
где S — площадь поперечного сечения проводника. Связь плотности тока со средней скоростью < v >направленного движения заряженных частиц
где q — заряд частицы; п — концентрация заряженных частиц. Закон Ома: а) где —j 1 -j 2 =U разность потенциалов (напряжение) на концах участка цепи; R — сопротивление участка; б) где E — ЭДС источника тока; R — полное сопротивление участка (сумма внешних и внутренних сопротивлений); в) где R — внешнее сопротивление цепи; r — внутреннее сопротивление цепи. Правила Кирхгофа: а) б) где Сопротивление R и проводимость G проводника
где r — удельное электрическое сопротивление; g — удельная электрическая проводимость; l — длина проводника; S — площадь поперечного сечения проводника. Сопротивление системы проводников: а) б) где R i — сопротивление i-го проводника. Работа тока:
Мощность тока:
Закон Джоуля—Ленца
Закон Ома в дифференциальной форме
где g — удельная электрическая проводимость; Е — напряженность электрического поля; j — плотность тока.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.008 с.) |


 ,
,
 .
.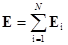


 .
. (при r<R),
(при r<R),
 .
. .
. (в вакууме),
(в вакууме), (при наличии диэлектрика),
(при наличии диэлектрика),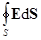 и
и  – потоки векторов E и D через поверхность S.
– потоки векторов E и D через поверхность S. ,
,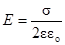 .
. или
или 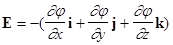 в общем случае (i,j,k – единичные вектора, направленные вдоль осей X,Y,Z, соответственно);
в общем случае (i,j,k – единичные вектора, направленные вдоль осей X,Y,Z, соответственно); в случае поля, обладающего центральной или осевой симметрией.
в случае поля, обладающего центральной или осевой симметрией. ,
, или
или  .
. или
или 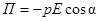 ,
, ,
, — при последовательном соединении;
— при последовательном соединении; — при параллельном соединении.
— при параллельном соединении.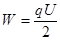 ,
, 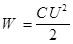 ,
,  .
.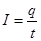 ,
, ,
, ,
, для однородного участка цепи (не содержащегоЭДС),
для однородного участка цепи (не содержащегоЭДС), для неоднородного участка цепи (участка, содержащего ЭДС),
для неоднородного участка цепи (участка, содержащего ЭДС), для замкнутой (полной) цепи,
для замкнутой (полной) цепи, — первое правило;
— первое правило; — второе правило,
— второе правило, — алгебраическая сумма сил токов, сходящихся в узле;
— алгебраическая сумма сил токов, сходящихся в узле;  — алгебраическая сумма произведений сил токов на сопротивления участков в замкнутом контуре;
— алгебраическая сумма произведений сил токов на сопротивления участков в замкнутом контуре;  — алгебраическая сумма ЭДС в замкнутом контуре.
— алгебраическая сумма ЭДС в замкнутом контуре. ,
,  ,
, при последовательном соединении;
при последовательном соединении; при параллельном соединении,
при параллельном соединении, .
. .
. .
. ,
,


