Напряженность и потенциал поля системы зарядов
Похожие статьи вашей тематики
| Система зарядов
| Напряженность поля
| Потенциал поля
| Точечный заряд 
| 
| 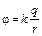
| Бесконечный заряженный прямолинейный проводник,  – линейная плотность заряда (Кл/м), – линейная плотность заряда (Кл/м),  – расстояние от проводника до точки поля, – расстояние от проводника до точки поля, 
| 
| 
| Бесконечная заряженная плоскость,  – поверхностная плотность заряда (Кл/м2), х – расстояние от плоскости до точки поля – поверхностная плотность заряда (Кл/м2), х – расстояние от плоскости до точки поля
| 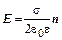
| 
|
Емкость плоского конденсатора
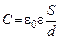 , ,
где  – площадь пластины конденсатора; – площадь пластины конденсатора;  – расстояние между пластинами; – расстояние между пластинами; 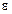 – относительная диэлектрическая проницаемость среды между пластинами конденсатора. Энергия электрического поля, запасенная конденсатором, равна – относительная диэлектрическая проницаемость среды между пластинами конденсатора. Энергия электрического поля, запасенная конденсатором, равна
 . .
Здесь 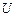 – разность потенциалов между пластинами конденсатора. – разность потенциалов между пластинами конденсатора.
Емкость С параллельно соединенных конденсаторов:
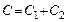 . .
Емкость С последовательно соединенных конденсаторов:
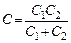 . .
Электрический ток
Закон Ома для однородного (нет источников тока) участка цепи в дифференциальной форме
 , ,
где  – плотность тока; – плотность тока;  – напряженность электрического поля между концами проводника; – напряженность электрического поля между концами проводника;  – удельная проводимость проводника. – удельная проводимость проводника.
Сила тока  определяется как определяется как
 . .
Разность потенциалов на концах однородного проводника определяется как
 . .
Электрическое сопротивление проводника
 , ,
где  – длина проводника; – длина проводника;  – площадь поперечного сечения проводника; – площадь поперечного сечения проводника;  – удельное сопротивление проводника, – удельное сопротивление проводника,  . .
Закон Ома для однородного участка цепи в интегральной форме
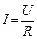 . .
Закон Ома для замкнутой цепи в интегральной форме
 . .
Здесь 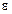 – ЭДС (электродвижущая сила) источника тока; – ЭДС (электродвижущая сила) источника тока;  – внутреннее сопротивление источника тока; – внутреннее сопротивление источника тока;  – внешнее сопротивление цепи. – внешнее сопротивление цепи.
Сопротивление  последовательно соединенных сопротивлений (резисторов): последовательно соединенных сопротивлений (резисторов):
 . .
Сопротивление  параллельно соединенных сопротивлений (резисторов): параллельно соединенных сопротивлений (резисторов):
 . .
Закон Джоуля–Ленца в интегральной форме
Количество теплоты, выделяющееся во всей замкнутой цепи:
 . .
Количество теплоты, выделяющееся на внешнем участке цепи:
 . .
Коэффициент полезного действия:
 . .
Примеры решения задач
Пример 1. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен под углом 45º к горизонту. Из орудия производят выстрел вдоль железнодорожного пути. Масса снаряда  кг и его скорость кг и его скорость  м/с, масса платформы с орудием м/с, масса платформы с орудием  тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен  ? ?
Решение
Считаем систему «снаряд–орудие» замкнутой в горизонтальном направлении. так как сумма проекций на 0 Х всех сил, действующих на систему, равна нулю, следовательно, можно применить закон сохранения импульса в горизонтальном направлении:
 . .

Проектируем скорости на горизонтальную ось, и для скорости  платформы получаем: платформы получаем:
 . .
Из закона сохранения энергии приращение кинетической энергии идет за счет работы сил, действующих на тело. В данном примере только сила трения вызывает изменение скорости платформы с орудием:
 . .
Так как  , то работа силы трения равна , то работа силы трения равна
 , ,
в нашем случае  . .
Сила трения  , ,   . Итак, подставляем заготовки: . Итак, подставляем заготовки:

С учетом выражения для скорости получаем расчетную формулу
 м м
Ответ: платформа с орудием откатилась на 32,7 м.
Пример 2. Газовый термометр состоит из шара (см. рисунок) с припаянной к нему горизонтальной стеклянной трубкой. Капелька ртути, помещенная в трубку, отделяет объем шара с газом от атмосферы. Площадь поперечного сечения трубки S = 0,1 см2. При T 1 = 273 К капелька ртути находилась на расстоянии x 1 = 30 см от поверхности шара, при T 2 = 278 К – на расстоянии x 2 = 50 см. Найдите объем шара V. Давление считайте постоянным.
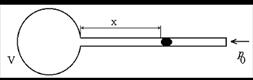
Решение
Во время измерения считается, что внешнее давление не изменяется и поскольку система находится в состоянии термодинамического равновесия, то давление внутри термометра равно внешнему давлению  , следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния: , следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния:
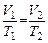 , (1) , (1)
где  , ,  . Подставляем выражения для V 1 и V 2 в (1) и получаем . Подставляем выражения для V 1 и V 2 в (1) и получаем
 . (2) . (2)
Размерности левой и правой частей, как легко убедиться, совпадают.
Подставляем численные значения физических величин в (2) и получаем:

Ответ: объём пустотелого шара равен 0,106 л.
Пример 3. Обмотка электрического кипятильника имеет две секции. Если включена только первая секция, то вода закипает через 15 минут, если только вторая, то через 30 минут. Через сколько минут закипит вода, если обе секции включить последовательно? параллельно?
Решение
сетевое напряжение не изменяется при параллельном подключении различных электрических устройств. применяем закон Джоуля–Ленца в форме
 , ,
где 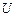 – постоянно, количество энергии – постоянно, количество энергии 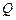 , необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что , необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что
 . .
а) последовательное соединение секций

б) параллельное соединение секций

Ответ: вода закипает: а) при последовательном соединении секций через 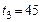 минут; б) при параллельном соединении секций минут; б) при параллельном соединении секций  минут. минут.
Содержание контрольной работы № 1
| Содержание
| Номера задач
| |
| Кинематика поступательного и вращательного движения материальной точки
| 101–110
| |
| Импульс и энергия материальной точки. Закон сохранения импульса и энергии. Работа.
| 111–120
| |
| Вращательное движение твердого тела. Закон сохранения момента импульса
| 121–130
| |
| Молекулярная физика и термодинамика
| 131–140
| |
| Закон Кулона. Напряженность. Суперпозиция полей
| 141–150
| |
| Потенциал, разность потенциалов. Работа перемещения зарядов в электростатическом поле
| 151–160
| |
| Электрическая емкость. Конденсаторы
| 161–170
| |
| Постоянный ток
| 171–180
| 11. Таблица вариантов задач
к контрольной работе № 1
Задачи
101. Материальная точка движется прямолинейно. Уравнение движения имеет вид  , где , где  , ,  . Найти скорость и ускорение точки в момент времени . Найти скорость и ускорение точки в момент времени  и и  . Каково среднее значение скорости за первые . Каково среднее значение скорости за первые  движения? движения?
102. Уравнение движения материальной точки вдоль оси ОХ имеет вид 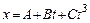 , где , где  , ,  , ,  . Найти координату х, скорость Vx и ускорение ах в момент времени . Найти координату х, скорость Vx и ускорение ах в момент времени  . .
103. Тело вращается вокруг неподвижной оси по закону  , где , где  , ,  , ,  . Найти полное ускорение точки, находящейся на расстоянии . Найти полное ускорение точки, находящейся на расстоянии  от оси вращения, в момент времени от оси вращения, в момент времени  . .
104. По прямой линии движутся две материальные точки согласно уравнениям:  и и  , где , где  , ,  , ,  , , 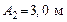 , , 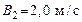 , ,  . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени  . .
105. Определить полное ускорение а в момент времени  точки, находящейся на ободе колеса радиусом точки, находящейся на ободе колеса радиусом 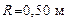 , вращающегося согласно уравнению , вращающегося согласно уравнению  , где , где 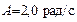 , ,  . .
106. Тело вращается вокруг неподвижной оси по закону  , где , где  , ,  . Через какое время тело остановится и сколько оборотов сделает до остановки? . Через какое время тело остановится и сколько оборотов сделает до остановки?
107. Сколько оборотов сделало тело за время, в течение которого частота увеличилась от 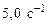 до до  ? Угловое ускорение равно ? Угловое ускорение равно  . .
108. Тело вращается равноускоренно с начальной угловой скоростью 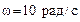 и угловым ускорением и угловым ускорением  . Сколько оборотов сделает тело за время . Сколько оборотов сделает тело за время 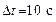 от начала движения? от начала движения?
109. Диск радиусом  , находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением , находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением  . Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения? . Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения?
110. Движение материальной точки описывается уравнением 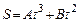 , где , где  , ,  . Найти скорость и ускорение точки в момент времени . Найти скорость и ускорение точки в момент времени  и среднюю скорость за первые две секунды движения. и среднюю скорость за первые две секунды движения.
111. Шарик массой 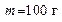 , летевший со скоростью , летевший со скоростью 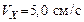 под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой. под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой.
112. Масса железнодорожной платформы вместе с жестко закрепленным на ней орудием  . Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда . Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда  и он вылетает из ствола орудия со скоростью и он вылетает из ствола орудия со скоростью  ? ?
113. Снаряд, летевший горизонтально со скоростью  , разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью , разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью  . Определить скорость . Определить скорость  большего осколка. большего осколка.
114. Человек массой  , бегущий со скоростью , бегущий со скоростью 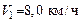 , догоняет тележку массой , догоняет тележку массой  , движущуюся со скоростью , движущуюся со скоростью 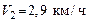 , и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу? , и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу?
115. Стальной шарик массой  , падая с высоты , падая с высоты  на стальную плиту, отскакивает от нее на высоту на стальную плиту, отскакивает от нее на высоту  . Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком. . Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком.
116. Шар массой  движется со скоростью движется со скоростью 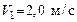 и сталкивается с покоящимся шаром массой и сталкивается с покоящимся шаром массой  . Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным. . Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
117. Шар массой  движется со скоростью движется со скоростью  и сталкивается с шаром массой и сталкивается с шаром массой  , который движется ему навстречу со скоростью , который движется ему навстречу со скоростью  . Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным. . Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
118. Конькобежец массой 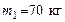 , стоя на коньках на льду, бросает в горизонтальном направлении камень массой , стоя на коньках на льду, бросает в горизонтальном направлении камень массой  со скоростью со скоростью  . Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед . Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед  . .
119. Вагон массой  , двигавшийся со скоростью , двигавшийся со скоростью  , налетев на пружинный буфер, остановился, сжав пружины на , налетев на пружинный буфер, остановился, сжав пружины на  . Найти общую жесткость k пружин буфера. . Найти общую жесткость k пружин буфера.
120. Шар массой 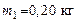 , движущийся со скоростью , движущийся со скоростью 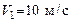 , ударяет неподвижный шар массой , ударяет неподвижный шар массой 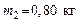 . Удар прямой, абсолютно упругий. Каковы будут скорости шаров после удара? . Удар прямой, абсолютно упругий. Каковы будут скорости шаров после удара?
121. На вал диаметром  намотан шнур, к которому привязан груз массой намотан шнур, к которому привязан груз массой  . Опускаясь равноускоренно, груз прошел путь . Опускаясь равноускоренно, груз прошел путь  за за  . Определить момент инерции маховика. . Определить момент инерции маховика.
122. Маховик в виде сплошного диска равномерно вращается вокруг оси, проходящей через его центр перпендикулярно поверхности диска. Под действием тормозящего момента  маховик останавливается, сделав маховик останавливается, сделав  оборотов. С какой частотой вращался диск, если его масса оборотов. С какой частотой вращался диск, если его масса  , а радиус , а радиус  . .
123. Тонкостенный цилиндр, масса которого  , а диаметр , а диаметр  , вращается согласно уравнению , вращается согласно уравнению 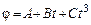 , где , где 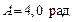 , ,  , , 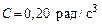 . Определить действующий на цилиндр момент сил в момент времени . Определить действующий на цилиндр момент сил в момент времени  . .
124. Определить момент силы, который необходимо приложить к блоку, вращающемуся с частотой  , чтобы он остановился в течение времени , чтобы он остановился в течение времени  . Диаметр блока . Диаметр блока  . Массу блока . Массу блока 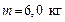 считать равномерно распределенной по ободу. считать равномерно распределенной по ободу.
125. Маховик, момент инерции которого 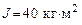 , начал вращаться равноускоренно из состояния покоя под действием момента сил , начал вращаться равноускоренно из состояния покоя под действием момента сил 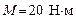 . Равноускоренное движение продолжалось в течение . Равноускоренное движение продолжалось в течение  . Определить кинетическую энергию, приобретенную маховиком. . Определить кинетическую энергию, приобретенную маховиком.
126. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению  , где , где  , , 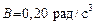 . Определить вращающий момент, действующий на стержень через . Определить вращающий момент, действующий на стержень через  после начала вращения, если момент инерции стержня после начала вращения, если момент инерции стержня  . .
127. На обод маховика диаметром  намотан шнур, к которому привязан груз массой намотан шнур, к которому привязан груз массой 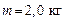 . Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за время . Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за время  приобрел угловую скорость приобрел угловую скорость  . .
128. Платформа в виде однородного диска радиусом 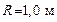 и массой и массой 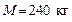 вращается по инерции с частотой вращается по инерции с частотой  . На краю платформы стоит человек, масса которого . На краю платформы стоит человек, масса которого  . С какой частотой будет вращаться платформа, если человек перейдет в еe центр? Какую работу совершит при этом человек? Момент инерции человека рассчитывать как для материальной точки. . С какой частотой будет вращаться платформа, если человек перейдет в еe центр? Какую работу совершит при этом человек? Момент инерции человека рассчитывать как для материальной точки.
 129. На краю скамьи Жуковского (см. рисунок) диаметром 129. На краю скамьи Жуковского (см. рисунок) диаметром  и массой и массой  стоит человек массой стоит человек массой 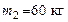 . С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой . С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой  ? Траектория мяча горизонтальна и проходит на расстоянии ? Траектория мяча горизонтальна и проходит на расстоянии 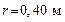 от оси скамьи. Скорость мяча от оси скамьи. Скорость мяча  . .
130. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси вращения. Скамья с человеком вращается с угловой скоростью  . С какой угловой скоростью . С какой угловой скоростью  будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Какую работу при этом совершает человек? Суммарный момент инерции человека и скамьи будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Какую работу при этом совершает человек? Суммарный момент инерции человека и скамьи  . Длина стержня . Длина стержня 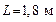 , масса , масса 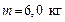 . Считать, что центр масс стержня с человеком находится на оси платформы. . Считать, что центр масс стержня с человеком находится на оси платформы.
131. Определить концентрацию молекул 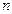 кислорода, находящегося в сосуде вместимостью кислорода, находящегося в сосуде вместимостью  . Количество вещества кислорода составляет . Количество вещества кислорода составляет  . .
132. Сколько молекул содержит  водяного пара? водяного пара?
133. В сосуде вместимостью  находится кислород* при температуре находится кислород* при температуре  . Когда часть газа израсходовали, давление в баллоне понизилось на . Когда часть газа израсходовали, давление в баллоне понизилось на  . Определить массу израсходованного кислорода. Процесс считать изотермическим. . Определить массу израсходованного кислорода. Процесс считать изотермическим.
134. В сосуде емкостью  находится азот при температуре находится азот при температуре  . Вследствие утечки газа давление уменьшилось на . Вследствие утечки газа давление уменьшилось на  . Определить массу газа, вышедшего из баллона. Температуру считать неизменной. . Определить массу газа, вышедшего из баллона. Температуру считать неизменной.
135. Определить массу газа в баллоне емкостью  при температуре при температуре  и давлении и давлении  , если его плотность при нормальных условиях , если его плотность при нормальных условиях 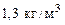 . .
136. Объем водорода при изотермическом расширении ( ) увеличился в ) увеличился в  раза. Определить работу, совершенную газом, и теплоту, полученную им при этом. Масса водорода равна раза. Определить работу, совершенную газом, и теплоту, полученную им при этом. Масса водорода равна  . .
137.  азота охлаждают при постоянном давлении от азота охлаждают при постоянном давлении от  до до 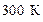 . Определить изменение внутренней энергии, работу и количество выделенной теплоты. . Определить изменение внутренней энергии, работу и количество выделенной теплоты.
138. Кислород массой 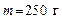 , имевший температуру , имевший температуру  , был адиабатически сжат. При этом была совершена работа , был адиабатически сжат. При этом была совершена работа  . Определить конечную температуру газа. . Определить конечную температуру газа.
139. При изотермическом сжатии давление азота массой 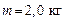 было увеличено от было увеличено от  до до  . Определить изменение энтропии газа. . Определить изменение энтропии газа.
140. Азот массой  был изобарически нагрет от был изобарически нагрет от  до до  . Определить работу, совершенную газом, полученную им при этом теплоту и изменение внутренней энергии газа. . Определить работу, совершенную газом, полученную им при этом теплоту и изменение внутренней энергии газа.
141. Два одинаковых положительных заряда  находятся в воздухе на расстоянии находятся в воздухе на расстоянии 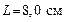 друг от друга. Определить напряженность электростатического поля: а) в точке О, находящейся на середине отрезка, соединяющего заряды; б) в точке А, расположенной на расстоянии друг от друга. Определить напряженность электростатического поля: а) в точке О, находящейся на середине отрезка, соединяющего заряды; б) в точке А, расположенной на расстоянии  от каждого заряда. от каждого заряда.
142. Два положительных точечных заряда  и и 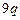 закреплены на расстоянии закреплены на расстоянии  . Где между ними, какой по величине и знаку заряд надо поместить, чтобы он находился в устойчивом равновесии? . Где между ними, какой по величине и знаку заряд надо поместить, чтобы он находился в устойчивом равновесии?
143. Отрицательный заряд  и положительный и положительный  закреплены на расстоянии закреплены на расстоянии  друг от друга. Где на линии, соединяющей заряды, следует поместить заряд друг от друга. Где на линии, соединяющей заряды, следует поместить заряд 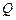 , чтобы он находился в равновесии? , чтобы он находился в равновесии?
144. Два отрицательно заряженных шарика, расположенных на расстоянии 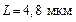 , взаимодействуют с силой , взаимодействуют с силой  . Найти число «избыточных» электронов на каждом шарике считая их заряды равными. Шарики принять за материальные точки. . Найти число «избыточных» электронов на каждом шарике считая их заряды равными. Шарики принять за материальные точки.
145. Два равных по величине положительных заряда 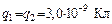 расположены в вершинах острых углов равнобедренного прямоугольного треугольника на расстоянии расположены в вершинах острых углов равнобедренного прямоугольного треугольника на расстоянии  . Определить, с какой силой оба заряда действуют на третий заряд . Определить, с какой силой оба заряда действуют на третий заряд  , находящийся в вершине прямого угла треугольника. Ответ поясните рисунком. , находящийся в вершине прямого угла треугольника. Ответ поясните рисунком.
146. Три одинаковых заряда  находятся в вершинах равностороннего треугольника со стороной находятся в вершинах равностороннего треугольника со стороной  . Определить силу . Определить силу  , действующую на один из этих зарядов. , действующую на один из этих зарядов.
147. В вершинах квадрата со стороной  находятся одинаковые положительные заряды находятся одинаковые положительные заряды 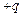 . Какой заряд . Какой заряд 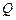 необходимо поместить в центр квадрата, чтобы вся система зарядов находилась в равновесии? необходимо поместить в центр квадрата, чтобы вся система зарядов находилась в равновесии?
148. Определить напряженность электростатического поля в центре шестиугольника со стороной  , в вершинах которого расположены: , в вершинах которого расположены:
а) равные заряды одного знака; б) заряды, равные по модулю, но чередующиеся по знаку.
149. В вершинах шестиугольника расположены точечные заряды  , ,  , , 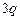 , , 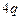 , ,  , ,  ( ( ). Найти силу, действующую на точечный заряд ). Найти силу, действующую на точечный заряд  , лежащий в центре шестиугольника. Ответ поясните рисунком. , лежащий в центре шестиугольника. Ответ поясните рисунком.
150. Два шарика массой  каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити  . Какие одинаковые заряды необходимо сообщить шарикам, чтобы нити разошлись на угол . Какие одинаковые заряды необходимо сообщить шарикам, чтобы нити разошлись на угол  ? ?
151.Тонкий стержень согнут в кольцо радиусом  . Он заряжен с линейной плотностью заряда . Он заряжен с линейной плотностью заряда  . Какую работу необходимо совершить, чтобы перенести заряд . Какую работу необходимо совершить, чтобы перенести заряд  из центра кольца в точку А, расположенную на оси кольца на расстоянии из центра кольца в точку А, расположенную на оси кольца на расстоянии 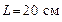 от его центра? от его центра?
152. Положительные заряды  и и  находятся в вакууме на расстоянии находятся в вакууме на расстоянии  друг от друга. Определить работу, которую необходимо совершить, чтобы сблизить заряды до расстояния друг от друга. Определить работу, которую необходимо совершить, чтобы сблизить заряды до расстояния  . .
153. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда  . Определить разность потенциалов двух точек поля, отстоящих от плоскости на расстояния . Определить разность потенциалов двух точек поля, отстоящих от плоскости на расстояния  и и 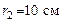 . .
154. Тонкий стержень согнут в кольцо радиусом  . Он заряжен с линейной плотностью заряда . Он заряжен с линейной плотностью заряда 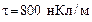 . Определить потенциал . Определить потенциал  в точке, расположенной на оси кольца на расстоянии в точке, расположенной на оси кольца на расстоянии  от его центра. от его центра.
155. На расстоянии  от бесконечно длинной заряженной нити находится точечный заряд от бесконечно длинной заряженной нити находится точечный заряд  . Под действием поля заряд приближается к нити до расстояния . Под действием поля заряд приближается к нити до расстояния  . При этом совершается работа . При этом совершается работа  . Найти линейную плотность заряда . Найти линейную плотность заряда  на нити. на нити.
156. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью заряда 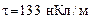 . Какую работу необходимо совершить, чтобы перенести заряд . Какую работу необходимо совершить, чтобы перенести заряд  из центра кольца в бесконечность? из центра кольца в бесконечность?
157. Равномерно заряженная бесконечно протяженная плоскость с поверхностной плотностью заряда  и точечный заряд и точечный заряд  находятся на расстоянии находятся на расстоянии 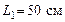 . Какую работу необходимо совершить, чтобы сблизить их до расстояния . Какую работу необходимо совершить, чтобы сблизить их до расстояния 
158. На тонком кольце радиусом  равномерно распределен заряд равномерно распределен заряд  . Какую наименьшую скорость необходимо сообщить находящемуся в центре кольца маленькому шарику массой . Какую наименьшую скорость необходимо сообщить находящемуся в центре кольца маленькому шарику массой  с зарядом с зарядом  , чтобы он мог удалиться из центра кольца на бесконечность? , чтобы он мог удалиться из центра кольца на бесконечность?
159. В однородное электрическое поле напряженностью  влетает (вдоль силовой линии) электрон со скоростью влетает (вдоль силовой линии) электрон со скоростью 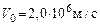 . Определить расстояние . Определить расстояние  , которое пройдет электрон до точки, где его скорость будет равна половине начальной. , которое пройдет электрон до точки, где его скорость будет равна половине начальной.
160. Шарик массой 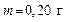 и зарядом и зарядом  перемещается из одной точки поля с потенциалом перемещается из одной точки поля с потенциалом 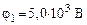 в другую с потенциалом в другую с потенциалом  . Найти скорость шарика в первой точке, если во второй точке она стала равной . Найти скорость шарика в первой точке, если во второй точке она стала равной  . .
161. Найти работу, которую нужно затратить, чтобы вынуть диэлектрик из плоского конденсатора, если напряжение на обкладках поддерживается постоянным и равным  . Площадь каждой пластины . Площадь каждой пластины  , расстояние между пластинами , расстояние между пластинами  , а диэлектрическая проницаемость диэлектрика , а диэлектрическая проницаемость диэлектрика 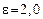 . .
162. Найти работу, которую нужно затратить, чтобы вынуть диэлектрик из плоского конденсатора, если заряд на обкладках поддерживается постоянным и равным  . Площадь каждой пластины . Площадь каждой пластины  , расстояние между пластинами , расстояние между пластинами 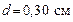 , а диэлектрическая проницаемость диэлектрика , а диэлектрическая проницаемость диэлектрика 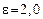 . .
163. Найти работу, которую нужно затратить, чтобы увеличить расстояние между пластинами плоского воздушного конденсатора, заряженного разноименными зарядами  , на величину , на величину  . Площадь каждой пластины конденсатора . Площадь каждой пластины конденсатора  . .
164. Какую работу надо совершить, чтобы увеличить расстояние между пластинами плоского вакуумного конденсатора с площадью пластин  каждая от расстояния каждая от расстояния  до расс до расс
|





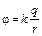
 – линейная плотность заряда (Кл/м),
– линейная плотность заряда (Кл/м),  – расстояние от проводника до точки поля,
– расстояние от проводника до точки поля, 


 – поверхностная плотность заряда (Кл/м2), х – расстояние от плоскости до точки поля
– поверхностная плотность заряда (Кл/м2), х – расстояние от плоскости до точки поля
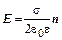

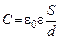 ,
, – площадь пластины конденсатора;
– площадь пластины конденсатора;  – расстояние между пластинами;
– расстояние между пластинами; 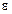 – относительная диэлектрическая проницаемость среды между пластинами конденсатора. Энергия электрического поля, запасенная конденсатором, равна
– относительная диэлектрическая проницаемость среды между пластинами конденсатора. Энергия электрического поля, запасенная конденсатором, равна .
.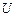 – разность потенциалов между пластинами конденсатора.
– разность потенциалов между пластинами конденсатора.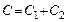 .
.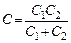 .
. ,
, – плотность тока;
– плотность тока;  – напряженность электрического поля между концами проводника;
– напряженность электрического поля между концами проводника;  – удельная проводимость проводника.
– удельная проводимость проводника. определяется как
определяется как .
. .
. ,
, – длина проводника;
– длина проводника;  – удельное сопротивление проводника,
– удельное сопротивление проводника,  .
.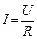 .
. .
. – внутреннее сопротивление источника тока;
– внутреннее сопротивление источника тока;  – внешнее сопротивление цепи.
– внешнее сопротивление цепи. .
. .
. .
. .
. .
. кг и его скорость
кг и его скорость  м/с, масса платформы с орудием
м/с, масса платформы с орудием  тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен
тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен  ?
? .
.
 платформы получаем:
платформы получаем: .
. .
. , то работа силы трения равна
, то работа силы трения равна ,
, .
. ,
, 
 . Итак, подставляем заготовки:
. Итак, подставляем заготовки:
 м
м
 , следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния:
, следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния: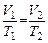 , (1)
, (1) ,
,  . Подставляем выражения для V 1 и V 2 в (1) и получаем
. Подставляем выражения для V 1 и V 2 в (1) и получаем . (2)
. (2)
 ,
,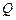 , необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что
, необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что .
.

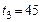 минут; б) при параллельном соединении секций
минут; б) при параллельном соединении секций  минут.
минут. , где
, где  ,
,  . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени  и
и  . Каково среднее значение скорости за первые
. Каково среднее значение скорости за первые  движения?
движения?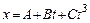 , где
, где  ,
,  ,
,  . Найти координату х, скорость Vx и ускорение ах в момент времени
. Найти координату х, скорость Vx и ускорение ах в момент времени  .
. , где
, где  ,
,  ,
,  . Найти полное ускорение точки, находящейся на расстоянии
. Найти полное ускорение точки, находящейся на расстоянии  от оси вращения, в момент времени
от оси вращения, в момент времени  .
. и
и  , где
, где  ,
,  ,
,  ,
, 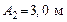 ,
, 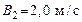 ,
,  . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени
. В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени  .
.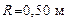 , вращающегося согласно уравнению
, вращающегося согласно уравнению  , где
, где 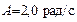 ,
,  .
. , где
, где  ,
,  . Через какое время тело остановится и сколько оборотов сделает до остановки?
. Через какое время тело остановится и сколько оборотов сделает до остановки?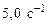 до
до  ? Угловое ускорение равно
? Угловое ускорение равно  .
.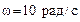 и угловым ускорением
и угловым ускорением  . Сколько оборотов сделает тело за время
. Сколько оборотов сделает тело за время 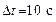 от начала движения?
от начала движения? , находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением
, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением  . Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения?
. Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения?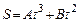 , где
, где  ,
,  . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени 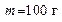 , летевший со скоростью
, летевший со скоростью 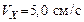 под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой.
под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой. . Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда
. Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда  и он вылетает из ствола орудия со скоростью
и он вылетает из ствола орудия со скоростью  ?
? , разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью
, разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью  . Определить скорость
. Определить скорость  большего осколка.
большего осколка. , бегущий со скоростью
, бегущий со скоростью 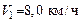 , догоняет тележку массой
, догоняет тележку массой  , движущуюся со скоростью
, движущуюся со скоростью 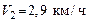 , и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу?
, и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу? , падая с высоты
, падая с высоты  на стальную плиту, отскакивает от нее на высоту
на стальную плиту, отскакивает от нее на высоту  . Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком.
. Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком. движется со скоростью
движется со скоростью 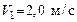 и сталкивается с покоящимся шаром массой
и сталкивается с покоящимся шаром массой  . Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным. движется со скоростью
движется со скоростью  и сталкивается с шаром массой
и сталкивается с шаром массой  , который движется ему навстречу со скоростью
, который движется ему навстречу со скоростью  . Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
. Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.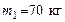 , стоя на коньках на льду, бросает в горизонтальном направлении камень массой
, стоя на коньках на льду, бросает в горизонтальном направлении камень массой  со скоростью
со скоростью  . Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед
. Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед  .
. , двигавшийся со скоростью
, двигавшийся со скоростью  , налетев на пружинный буфер, остановился, сжав пружины на
, налетев на пружинный буфер, остановился, сжав пружины на  . Найти общую жесткость k пружин буфера.
. Найти общую жесткость k пружин буфера.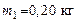 , движущийся со скоростью
, движущийся со скоростью 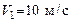 , ударяет неподвижный шар массой
, ударяет неподвижный шар массой 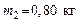 . Удар прямой, абсолютно упругий. Каковы будут скорости шаров после удара?
. Удар прямой, абсолютно упругий. Каковы будут скорости шаров после удара? намотан шнур, к которому привязан груз массой
намотан шнур, к которому привязан груз массой  . Опускаясь равноускоренно, груз прошел путь
. Опускаясь равноускоренно, груз прошел путь  за
за  . Определить момент инерции маховика.
. Определить момент инерции маховика. маховик останавливается, сделав
маховик останавливается, сделав  оборотов. С какой частотой вращался диск, если его масса
оборотов. С какой частотой вращался диск, если его масса  , а радиус
, а радиус  , а диаметр
, а диаметр  , вращается согласно уравнению
, вращается согласно уравнению 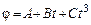 , где
, где 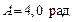 ,
,  ,
, 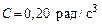 . Определить действующий на цилиндр момент сил в момент времени
. Определить действующий на цилиндр момент сил в момент времени  , чтобы он остановился в течение времени
, чтобы он остановился в течение времени  . Диаметр блока
. Диаметр блока 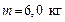 считать равномерно распределенной по ободу.
считать равномерно распределенной по ободу.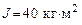 , начал вращаться равноускоренно из состояния покоя под действием момента сил
, начал вращаться равноускоренно из состояния покоя под действием момента сил 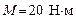 . Равноускоренное движение продолжалось в течение
. Равноускоренное движение продолжалось в течение  . Определить кинетическую энергию, приобретенную маховиком.
. Определить кинетическую энергию, приобретенную маховиком. , где
, где  ,
, 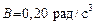 . Определить вращающий момент, действующий на стержень через
. Определить вращающий момент, действующий на стержень через  .
. намотан шнур, к которому привязан груз массой
намотан шнур, к которому привязан груз массой 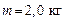 . Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за время
. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за время  .
.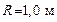 и массой
и массой 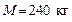 вращается по инерции с частотой
вращается по инерции с частотой  . На краю платформы стоит человек, масса которого
. На краю платформы стоит человек, масса которого  . С какой частотой будет вращаться платформа, если человек перейдет в еe центр? Какую работу совершит при этом человек? Момент инерции человека рассчитывать как для материальной точки.
. С какой частотой будет вращаться платформа, если человек перейдет в еe центр? Какую работу совершит при этом человек? Момент инерции человека рассчитывать как для материальной точки. 129. На краю скамьи Жуковского (см. рисунок) диаметром
129. На краю скамьи Жуковского (см. рисунок) диаметром  и массой
и массой  стоит человек массой
стоит человек массой 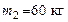 . С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой
. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой  ? Траектория мяча горизонтальна и проходит на расстоянии
? Траектория мяча горизонтальна и проходит на расстоянии 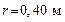 от оси скамьи. Скорость мяча
от оси скамьи. Скорость мяча  .
. . С какой угловой скоростью
. С какой угловой скоростью  будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Какую работу при этом совершает человек? Суммарный момент инерции человека и скамьи
будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Какую работу при этом совершает человек? Суммарный момент инерции человека и скамьи  . Длина стержня
. Длина стержня 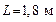 , масса
, масса 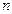 кислорода, находящегося в сосуде вместимостью
кислорода, находящегося в сосуде вместимостью  . Количество вещества кислорода составляет
. Количество вещества кислорода составляет  .
. водяного пара?
водяного пара? находится кислород* при температуре
находится кислород* при температуре  . Когда часть газа израсходовали, давление в баллоне понизилось на
. Когда часть газа израсходовали, давление в баллоне понизилось на  . Определить массу израсходованного кислорода. Процесс считать изотермическим.
. Определить массу израсходованного кислорода. Процесс считать изотермическим. находится азот при температуре
находится азот при температуре  . Вследствие утечки газа давление уменьшилось на
. Вследствие утечки газа давление уменьшилось на  . Определить массу газа, вышедшего из баллона. Температуру считать неизменной.
. Определить массу газа, вышедшего из баллона. Температуру считать неизменной. при температуре
при температуре  и давлении
и давлении  , если его плотность при нормальных условиях
, если его плотность при нормальных условиях 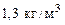 .
. раза. Определить работу, совершенную газом, и теплоту, полученную им при этом. Масса водорода равна
раза. Определить работу, совершенную газом, и теплоту, полученную им при этом. Масса водорода равна  .
. азота охлаждают при постоянном давлении от
азота охлаждают при постоянном давлении от  до
до 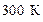 . Определить изменение внутренней энергии, работу и количество выделенной теплоты.
. Определить изменение внутренней энергии, работу и количество выделенной теплоты.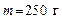 , имевший температуру
, имевший температуру  , был адиабатически сжат. При этом была совершена работа
, был адиабатически сжат. При этом была совершена работа  . Определить конечную температуру газа.
. Определить конечную температуру газа. до
до  . Определить изменение энтропии газа.
. Определить изменение энтропии газа. был изобарически нагрет от
был изобарически нагрет от  . Определить работу, совершенную газом, полученную им при этом теплоту и изменение внутренней энергии газа.
. Определить работу, совершенную газом, полученную им при этом теплоту и изменение внутренней энергии газа. находятся в воздухе на расстоянии
находятся в воздухе на расстоянии 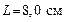 друг от друга. Определить напряженность электростатического поля: а) в точке О, находящейся на середине отрезка, соединяющего заряды; б) в точке А, расположенной на расстоянии
друг от друга. Определить напряженность электростатического поля: а) в точке О, находящейся на середине отрезка, соединяющего заряды; б) в точке А, расположенной на расстоянии  от каждого заряда.
от каждого заряда. и
и 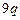 закреплены на расстоянии
закреплены на расстоянии  . Где между ними, какой по величине и знаку заряд надо поместить, чтобы он находился в устойчивом равновесии?
. Где между ними, какой по величине и знаку заряд надо поместить, чтобы он находился в устойчивом равновесии? и положительный
и положительный  закреплены на расстоянии
закреплены на расстоянии 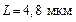 , взаимодействуют с силой
, взаимодействуют с силой  . Найти число «избыточных» электронов на каждом шарике считая их заряды равными. Шарики принять за материальные точки.
. Найти число «избыточных» электронов на каждом шарике считая их заряды равными. Шарики принять за материальные точки.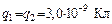 расположены в вершинах острых углов равнобедренного прямоугольного треугольника на расстоянии
расположены в вершинах острых углов равнобедренного прямоугольного треугольника на расстоянии  . Определить, с какой силой оба заряда действуют на третий заряд
. Определить, с какой силой оба заряда действуют на третий заряд  , находящийся в вершине прямого угла треугольника. Ответ поясните рисунком.
, находящийся в вершине прямого угла треугольника. Ответ поясните рисунком. находятся в вершинах равностороннего треугольника со стороной
находятся в вершинах равностороннего треугольника со стороной  . Определить силу
. Определить силу  , действующую на один из этих зарядов.
, действующую на один из этих зарядов. находятся одинаковые положительные заряды
находятся одинаковые положительные заряды 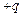 . Какой заряд
. Какой заряд  ,
, 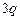 ,
, 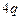 ,
,  ,
,  (
( ). Найти силу, действующую на точечный заряд
). Найти силу, действующую на точечный заряд  каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити
каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити  . Какие одинаковые заряды необходимо сообщить шарикам, чтобы нити разошлись на угол
. Какие одинаковые заряды необходимо сообщить шарикам, чтобы нити разошлись на угол  ?
? . Он заряжен с линейной плотностью заряда
. Он заряжен с линейной плотностью заряда  . Какую работу необходимо совершить, чтобы перенести заряд
. Какую работу необходимо совершить, чтобы перенести заряд  из центра кольца в точку А, расположенную на оси кольца на расстоянии
из центра кольца в точку А, расположенную на оси кольца на расстоянии 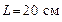 от его центра?
от его центра? и
и  находятся в вакууме на расстоянии
находятся в вакууме на расстоянии  друг от друга. Определить работу, которую необходимо совершить, чтобы сблизить заряды до расстояния
друг от друга. Определить работу, которую необходимо совершить, чтобы сблизить заряды до расстояния  .
. . Определить разность потенциалов двух точек поля, отстоящих от плоскости на расстояния
. Определить разность потенциалов двух точек поля, отстоящих от плоскости на расстояния  и
и 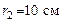 .
.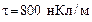 . Определить потенциал
. Определить потенциал  в точке, расположенной на оси кольца на расстоянии
в точке, расположенной на оси кольца на расстоянии  от его центра.
от его центра. от бесконечно длинной заряженной нити находится точечный заряд
от бесконечно длинной заряженной нити находится точечный заряд  . Под действием поля заряд приближается к нити до расстояния
. Под действием поля заряд приближается к нити до расстояния  . При этом совершается работа
. При этом совершается работа  . Найти линейную плотность заряда
. Найти линейную плотность заряда  на нити.
на нити.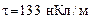 . Какую работу необходимо совершить, чтобы перенести заряд
. Какую работу необходимо совершить, чтобы перенести заряд  из центра кольца в бесконечность?
из центра кольца в бесконечность? и точечный заряд
и точечный заряд  находятся на расстоянии
находятся на расстоянии 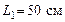 . Какую работу необходимо совершить, чтобы сблизить их до расстояния
. Какую работу необходимо совершить, чтобы сблизить их до расстояния 
 . Какую наименьшую скорость необходимо сообщить находящемуся в центре кольца маленькому шарику массой
. Какую наименьшую скорость необходимо сообщить находящемуся в центре кольца маленькому шарику массой  с зарядом
с зарядом  , чтобы он мог удалиться из центра кольца на бесконечность?
, чтобы он мог удалиться из центра кольца на бесконечность? влетает (вдоль силовой линии) электрон со скоростью
влетает (вдоль силовой линии) электрон со скоростью 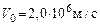 . Определить расстояние
. Определить расстояние  , которое пройдет электрон до точки, где его скорость будет равна половине начальной.
, которое пройдет электрон до точки, где его скорость будет равна половине начальной.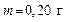 и зарядом
и зарядом  перемещается из одной точки поля с потенциалом
перемещается из одной точки поля с потенциалом 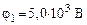 в другую с потенциалом
в другую с потенциалом  . Найти скорость шарика в первой точке, если во второй точке она стала равной
. Найти скорость шарика в первой точке, если во второй точке она стала равной  .
. . Площадь каждой пластины
. Площадь каждой пластины  , расстояние между пластинами
, расстояние между пластинами  , а диэлектрическая проницаемость диэлектрика
, а диэлектрическая проницаемость диэлектрика 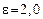 .
. . Площадь каждой пластины
. Площадь каждой пластины  , расстояние между пластинами
, расстояние между пластинами 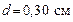 , а диэлектрическая проницаемость диэлектрика
, а диэлектрическая проницаемость диэлектрика  , на величину
, на величину  . Площадь каждой пластины конденсатора
. Площадь каждой пластины конденсатора  .
. до расс
до расс 


