
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика одномерного движенияСодержание книги
Поиск на нашем сайте
Закон движения материальной точки Скорость материальной точки:
Ускорение материальной точки
Средняя скорость
Равнопеременное движения материальной точки
Вращательное движение тела
Угловая скорость
Угловое ускорение
Связь линейной и угловой скорости
[…] – означает векторное произведение векторов, где r – радиус–вектор с началом в любой точке оси вращения. В случае равномерного вращения тела для любой точки нормальное ускорение
Тангенциальное ускорение
где R – расстояние от оси вращения.
Динамика
Второй закона Ньютона
где импульс Для системы из N материальных точек импульс системы равен
Поступательное движение системы характеризуется движением ее центра масс:
где где Сила гравитационного притяжения между двумя телами массой
где r – расстояние между центрами масс этих тел; Сила тяжести (для Земли)
где Сила трения скольжения
где
8.1.3. Законы сохранения энергии, импульса,
Элементарная работа силы F, затраченная на перемещение d l,
где Мощность силы
где Работа сил поля равна убыли потенциальной энергии частицы в данном поле:
Приращение кинетической энергии равно
где Приращение полной механической энергии
где Система называется замкнутой (изолированной), если она не обменивается с внешней средой энергией и веществом. В замкнутой системе полный импульс системы сохраняется:
Абсолютно упругий центральный удар двух тел
Пусть тела движутся вдоль линии, соединяющей их центры масс.
где
Абсолютно неупругий центральный удар двух тел
В этом случае тела после столкновения имеют одинаковые скорости
где
Механика твердого тела
Момент силы
где Момент импульса
где Изменение момента импульса определяется из уравнения
где Для замкнутой системы момент всех внешних сил равен нулю, тогда полный момент импульса сохраняется:
Для тела, вращающегося вокруг неподвижной оси
где Момент инерции I относительно произвольной оси определяется согласно теореме Штейнера
где Моменты инерции ряда тел приведены в табл. 1
Таблица 1 Момент инерции тела относительно оси z
Работа внешних сил при повороте тела вокруг неподвижной оси на угол
Кинетическая энергия тела, вращающегося относительно неподвижной оси
Кинетическая энергия тела при плоском движении
Момент импульса твердого тела относительно неподвижной оси
где
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.008 с.) |

 .
. .
. .
. .
. = const,
= const, ,
, .
. .
. .
. ,
, .
. ,
, или
или  ,
, равен
равен  ; F – равнодействующая всех сил, действующих на тело.
; F – равнодействующая всех сил, действующих на тело. .
. ,
, ,
,  ,
,  ,
,  ,
,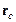 – радиус-вектор центра масс системы;
– радиус-вектор центра масс системы;  – радиус-вектор i -й частицы с массой
– радиус-вектор i -й частицы с массой  .
. и
и  равна
равна ,
, – постоянная тяготения.
– постоянная тяготения. ,
, м/с2 – ускорение свободного падения.
м/с2 – ускорение свободного падения. ,
, – коэффициент трения скольжения; N – сила нормального давления.
– коэффициент трения скольжения; N – сила нормального давления. ,
, – угол между F и d l.
– угол между F и d l. ,
, – угол между
– угол между 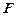 и
и  .
. .
. ,
, – работа всех сил, действующих на тело.
– работа всех сил, действующих на тело. равно
равно ,
,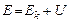 – полная механическая энергия;
– полная механическая энергия;  – работа внешних сил.
– работа внешних сил. .
. ,
, ,
, – скорости тел до столкновения;
– скорости тел до столкновения; 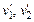 – скорости тел после столкновения.
– скорости тел после столкновения. :
: ,
, относительно некоторой точки О есть
относительно некоторой точки О есть ,
, – радиус-вектор, проведенный в точку приложения силы.
– радиус-вектор, проведенный в точку приложения силы. относительно некоторой точки О есть
относительно некоторой точки О есть ,
, ,
, .
. , уравнение динамики вращательного движения имеет вид
, уравнение динамики вращательного движения имеет вид или
или  ,
, – проекция углового ускорения на ось
– проекция углового ускорения на ось  – проекция суммарного момента внешних сил на ось
– проекция суммарного момента внешних сил на ось  – момент инерции тела относительно оси
– момент инерции тела относительно оси  .
. ,
, – момент инерции тела относительно оси, параллельной данной и проходящей через центр масс;
– момент инерции тела относительно оси, параллельной данной и проходящей через центр масс;  – расстояние между осями.
– расстояние между осями. (
( – кратчайшее расстояние от точки до оси)
– кратчайшее расстояние от точки до оси)











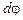
 .
. .
. .
. ,
, – момент импульса, момент инерции, угловая скорость относительно оси z.
– момент импульса, момент инерции, угловая скорость относительно оси z.


