
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 1 по физикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Список рекомендуемой литературы 1. Савельев И.В. Курс общей физики. Книга 1. Механика. – М.: Наука, 2003. 2. Савельев И.В. Курс общей физики. Книга 2. Электричество и магнетизм. – М.: Наука, 2003. 3. Савельев И.В. Курс общей физики. Книга 3. Молекулярная физика и термодинамика. – М.: Наука, 2003. 4. Детлаф А.В., Яворский Б.М. Курс физики. – М.: Высшая школа, 2002. 5. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2003. 6. Иродов И.Е. Основные законы механики. – М.: Высшая школа, 2002. 7. Иродов И.Е. Электромагнетизм. – М.: Высшая школа, 2002. 8. Давыдков В.В. Курс общей физики для студентов ИДО. Ч.1: Механика. Молекулярная физика и термодинамика. – Новосибирск: Изд-во НГТУ, 2001. 9. Давыдков В.В. Курс общей физики для студентов ИДО. Ч. 2: Электростатика. Магнетизм. Колебания и волны. – Новосибирск: Изд-во НГТУ, 2005. 6. Порядок оформления и решения задач 1. Контрольная работа выполняется в обычной школьной тетради, на обложке которой приводятся сведения по следующему образцу:
Контрольная работа № 1 по физике студента I курса ИДО НГТУ специальность: №________________ Иванова Петра Ивановича ( Ф.И.О. – без сокращений) Шифр 30675234 Вариант № 4
2. Контрольная работа выполняется ручкой cинего, фиолетового или черного цвета. Графики и рисунки аккуратно выполняются остро отточенным карандашом с использованием линейки и циркуля. Для замечаний преподавателя следует оставлять поля не менее 30 мм. 3. При оформлении контрольной работы условия задач записываются полностью, без сокращений. Каждая задача оформляется с новой страницы. 4. Решение задачи необходимо начинать с внимательного чтения условия. При первом же чтении следует определить, на какую тему, о каком конкретном процессе или состоянии идет речь, каким законам он подчиняется, какими параметрами его можно охарактеризовать. 5. Записывается краткое условие задачи: что «дано», что «найти». Все величины выражаются в единицах СИ. 6. Для того чтобы представить взаимодействие тел, их расположение, следует непременно сделать схематический чертеж (особенно это касается задач по «механике»), на котором показать заданные расстояния, векторы скоростей, перемещений, ускорений, действующих сил. Очень важным элементом является выбор системы отсчета: либо это система лабораторная, либо она связана с центром масс системы. Вид уравнений зависит от выбора системы отсчета. 7. Приводятся необходимые уравнения или формулы законов, описывающих процессы и явления, о которых идет речь в задаче. Составление системы уравнений, полностью отражающих конкретную ситуацию, физический процесс, является основной трудностью при решении задачи. • Исходные уравнения записываются в векторной форме (если речь идет о векторных уравнениях), а затем – в скалярной форме. • Если при решении задачи применяется формула, не выражающая собой основной закон (например, законы Ньютона, законы сохранения) или являющаяся хорошо известным следствием этих законов (например, теорема Штейнера, формула для кинетической энергии вращающегося тела и т.д.), то ее необходимо вывести. • Символическая запись законов, используемых для решения задачи, должна сопровождаться разъяснениями буквенных обозначений, формулировкой законов и условий, гарантирующих выполнение этих законов. 8. Вывод расчетной формулы осуществляется в общем виде (без промежуточных вычислений). Решить задачу в общем виде – это значит выразить искомую величину через те величины, которые заданы в условии задачи или справочных таблицах. 9. Полученная расчетная формула проверяется по размерности. Получение адекватных единиц измерения искомой величины служит одним из важнейших показателей правильности решения задачи. 10. Вычисление искомой величины осуществляется с учетом правил приближенных вычислений. 11. После получения численного значения оценивается его реальная величина (правдоподобность) исходя из соображений здравого смысла (встречаются ли в действительности такие численные значения искомой величины). 12. Записывается результат. О приближенных вычислениях
Значащими цифрами числа называют все цифры числа, кроме нулей слева. Например, в числе 3,25 три значащие цифры, 0,0325 – три значащие цифры, 0,030025 – пять значащих цифр, 3,00 – три значащих цифры. Выполняя вычисления, всегда необходимо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого. В настоящее время имеются различные счетно-вычислительные машинки, которые при вычислениях дают большое число значащих цифр. Очень часто студенты в своих работах по неопытности допускают ошибку, добиваясь при вычислениях результатов такой степени точности, которая не оправдывается точностью используемых данных. Для того чтобы не повторить этой ошибки, при решении задач следует придерживаться правил приближенных вычислений.
Правила округления
1. Если первая отбрасываемая цифра больше 5 или 5 с последующими цифрами, не равными нулю, то последняя сохраняемая цифра увеличивается на единицу. Например, число 3,56317 при округлении до десятых дает 3,6. 2. Если первая отбрасываемая цифра меньше 5, то последняя сохраняемая цифра не изменяется. Например, число 3,56317 при округлении до сотых дает 3,56. 3. Если первая отбрасываемая цифра 5 и за ней либо нет цифр, либо есть одни нули, то последняя сохраняемая цифра должна быть четной. Например, при округлении до десятых 3,5500 ≈ 3,6 и 3,65 ≈ 3,6.
Основные правила приближенных вычислений
1. При сложении и вычитании результат округляется так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одной из заданных величин; например, 7,852 + 3,18 – 4,3 = 6,732 ≈ 6,7(результат округлен до десятых по числу 4,3). 2. При умножении сомножители округляются так, чтобы каждый содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим их числом. Например, вместо (7,852×3,18×4,3) следует вычислять (7,9×3,2×4,3). В окончательном результате при этом следует оставлять такое же число значащих цифр, как и в сомножителях после округления: 7,852×3,18×4,3 ≈ 7,9×3,2×4,3 = 108,704 ≈ 1,1×102. 3. При делении необходимо соблюдать такое же правило, как и при умножении. Например, 7,852: 3,18 ≈ 7,85: 3,18 = 2,4685… ≈ 2,47. 4. При возведении числа в степень результат округляется таким образом, чтобы он имел столько значащих цифр, сколько их имеет основание степени. Например, 3,183 = 32,157432 ≈ 32,2. 5. При извлечении корня в результате указывается столько значащих цифр, сколько их в подкоренном выражении. Например, 6. При вычислении сложных выражений следует применять указанные выше правила в соответствии с видом производимых действий.
8. Основные определения и формулы
Механика
Кинематика Материальной точкой называется тело, размерами которого пренебрегают в условиях данной задачи. Положение материальной точки в пространстве задается ее радиусом-вектором
Зависимость Мгновенная скорость или просто скорость определяется так:
где Модуль скорости
Средняя скорость точки:
где Ускорение материальной точки
где компонента нормального ускорения имеет вид
а компонента касательного (тангенциального) ускорения имеет вид
Здесь Модуль ускорения
Динамика
Второй закона Ньютона
где импульс Для системы из N материальных точек импульс системы равен
Поступательное движение системы характеризуется движением ее центра масс:
где где Сила гравитационного притяжения между двумя телами массой
где r – расстояние между центрами масс этих тел; Сила тяжести (для Земли)
где Сила трения скольжения
где
8.1.3. Законы сохранения энергии, импульса,
Элементарная работа силы F, затраченная на перемещение d l,
где Мощность силы
где Работа сил поля равна убыли потенциальной энергии частицы в данном поле:
Приращение кинетической энергии равно
где Приращение полной механической энергии
где Система называется замкнутой (изолированной), если она не обменивается с внешней средой энергией и веществом. В замкнутой системе полный импульс системы сохраняется:
Абсолютно упругий центральный удар двух тел
Пусть тела движутся вдоль линии, соединяющей их центры масс.
где
Абсолютно неупругий центральный удар двух тел
В этом случае тела после столкновения имеют одинаковые скорости
где
Механика твердого тела
Момент силы
где Момент импульса
где Изменение момента импульса определяется из уравнения
где Для замкнутой системы момент всех внешних сил равен нулю, тогда полный момент импульса сохраняется:
Для тела, вращающегося вокруг неподвижной оси
где Момент инерции I относительно произвольной оси определяется согласно теореме Штейнера
где Моменты инерции ряда тел приведены в табл. 1
Таблица 1 Момент инерции тела относительно оси z
Работа внешних сил при повороте тела вокруг неподвижной оси на угол
Кинетическая энергия тела, вращающегося относительно неподвижной оси
Кинетическая энергия тела при плоском движении
Момент импульса твердого тела относительно неподвижной оси
где
Молярная масса для газов
Работа газа по расширению
Таблица 3 Электричество и магнетизм Электростатика
Точечный заряд – это заряженное тело, размером которого можно пренебречь по сравнению с расстояниями от этого тела до других заряженных тел. Закон Кулона
где Принцип суперпозиции
Если на точечный заряд действуют два и более зарядов, то результирующая сила равна
Напряженность электрического поля
где Напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, которые создает каждый заряд системы в отдельности:
Работа электрического поля по перемещению электрического
где потенциальная энергия заряда
а функция
Потенциал электрического поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых каждым из зарядов системы в отдельности:
Полная механическая энергия заряда, движущегося со скоростью
Электрический ток
Закон Ома для однородного (нет источников тока) участка цепи в дифференциальной форме
где Сила тока
Разность потенциалов на концах однородного проводника определяется как
Электрическое сопротивление проводника
где Закон Ома для однородного участка цепи в интегральной форме
Закон Ома для замкнутой цепи в интегральной форме
Здесь Сопротивление
Сопротивление
Примеры решения задач
Пример 1. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен под углом 45º к горизонту. Из орудия производят выстрел вдоль железнодорожного пути. Масса снаряда
Решение
Считаем систему «снаряд–орудие» замкнутой в горизонтальном направлении. так как сумма проекций на 0 Х всех сил, действующих на систему, равна нулю, следовательно, можно применить закон сохранения импульса в горизонтальном направлении:
Проектируем скорости на горизонтальную ось, и для скорости
Из закона сохранения энергии приращение кинетической энергии идет за счет работы сил, действующих на тело. В данном примере только сила трения вызывает изменение скорости платформы с орудием:
Так как
в нашем случае Сила трения
С учетом выражения для скорости получаем расчетную формулу
Ответ: платформа с орудием откатилась на 32,7 м.
Пример 2. Газовый термометр состоит из шара (см. рисунок) с припаянной к нему горизонтальной стеклянной трубкой. Капелька ртути, помещенная в трубку, отделяет объем шара с газом от атмосферы. Площадь поперечного сечения трубки S = 0,1 см2. При T 1 = 273 К капелька ртути находилась на расстоянии x 1 = 30 см от поверхности шара, при T 2 = 278 К – на расстоянии x 2 = 50 см. Найдите объем шара V. Давление считайте постоянным.
Решение Во время измерения считается, что внешнее давление не изменяется и поскольку система находится в состоянии термодинамического равновесия, то давление внутри термометра равно внешнему давлению
где
Размерности левой и правой частей, как легко убедиться, совпадают. Подставляем численные значения физических величин в (2) и получаем:
Ответ: объём пустотелого шара равен 0,106 л.
Пример 3. Обмотка электрического кипятильника имеет две секции. Если включена только первая секция, то вода закипает через 15 минут, если только вторая, то через 30 минут. Через сколько минут закипит вода, если обе секции включить последовательно? параллельно? Решение сетевое напряжение не изменяется при параллельном подключении различных электрических устройств. применяем закон Джоуля–Ленца в форме
где
а) последовательное соединение секций
б) параллельное соединение секций
Ответ: вода закипает: а) при последовательном соединении секций через Содержание контрольной работы № 1
11. Таблица вариантов задач
Задачи 101. Материальная точка движется прямолинейно. Уравнение движения имеет вид
102. Уравнение движения материальной точки вдоль оси ОХ имеет вид
103. Тело вращается вокруг неподвижной оси по закону
104. По прямой линии движутся две материальные точки согласно уравнениям:
105. Определить полное ускорение а в момент времени
106. Тело вращается вокруг неподвижной оси по закону
107. Сколько оборотов сделало тело за время, в течение которого частота увеличилась от 108. Тело вращается равноускоренно с начальной угловой скоростью
109. Диск радиусом
110. Движение материальной точки описывается уравнением
111. Шарик массой
112. Масса железнодорожной платформы вместе с жестко закрепленным на ней орудием
113. Снаряд, летевший горизонтально со скоростью
114. Человек массой
115. Стальной шарик массой
116. Шар массой
117. Шар массой
118. Конькобежец массой
119. Вагон массой | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 .
. :
: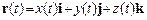 .
. ,
,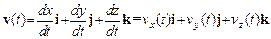 ,
, – единичные векторы декартовой системы координат.
– единичные векторы декартовой системы координат. .
. ,
, – длина пути, пройденного точкой за
– длина пути, пройденного точкой за  .
. ,
, ,
, ,
, .
. – локальный радиус кривизны траектории тела (при вращательном движении тела
– локальный радиус кривизны траектории тела (при вращательном движении тела  – единичный вектор, направленный вдоль вектора скорости.
– единичный вектор, направленный вдоль вектора скорости. .
. или
или  ,
, равен
равен  ; F – равнодействующая всех сил, действующих на тело.
; F – равнодействующая всех сил, действующих на тело. .
. ,
, ,
,  ,
,  ,
,  ,
,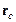 – радиус-вектор центра масс системы;
– радиус-вектор центра масс системы;  – радиус-вектор i -й частицы с массой
– радиус-вектор i -й частицы с массой  .
. и
и  равна
равна ,
, – постоянная тяготения.
– постоянная тяготения. ,
, м/с2 – ускорение свободного падения.
м/с2 – ускорение свободного падения. ,
, – коэффициент трения скольжения; N – сила нормального давления.
– коэффициент трения скольжения; N – сила нормального давления. ,
, – угол между F и d l.
– угол между F и d l. ,
, – угол между
– угол между 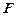 и
и  .
. .
. ,
, – работа всех сил, действующих на тело.
– работа всех сил, действующих на тело. равно
равно ,
,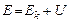 – полная механическая энергия;
– полная механическая энергия;  – работа внешних сил.
– работа внешних сил. .
. ,
, ,
, – скорости тел до столкновения;
– скорости тел до столкновения; 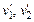 – скорости тел после столкновения.
– скорости тел после столкновения. :
: ,
, относительно некоторой точки О есть
относительно некоторой точки О есть ,
, – радиус-вектор, проведенный в точку приложения силы.
– радиус-вектор, проведенный в точку приложения силы. относительно некоторой точки О есть
относительно некоторой точки О есть ,
, ,
, .
. , уравнение динамики вращательного движения имеет вид
, уравнение динамики вращательного движения имеет вид или
или  ,
, – проекция углового ускорения на ось
– проекция углового ускорения на ось  – проекция суммарного момента внешних сил на ось
– проекция суммарного момента внешних сил на ось  – момент инерции тела относительно оси
– момент инерции тела относительно оси  .
. ,
, – момент инерции тела относительно оси, параллельной данной и проходящей через центр масс;
– момент инерции тела относительно оси, параллельной данной и проходящей через центр масс;  – расстояние между осями.
– расстояние между осями. (
( – кратчайшее расстояние от точки до оси)
– кратчайшее расстояние от точки до оси)











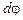
 .
. .
. .
. ,
, – момент импульса, момент инерции, угловая скорость относительно оси z.
– момент импульса, момент инерции, угловая скорость относительно оси z. .
. ,
,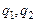 – электрические точечные заряды, Кл;
– электрические точечные заряды, Кл;  м/Ф;
м/Ф;  Ф/м;
Ф/м;  – расстояние между зарядами;
– расстояние между зарядами;  – единичный вектор, направленный вдоль радиуса-вектора.
– единичный вектор, направленный вдоль радиуса-вектора. .
. ,
, – положительный пробный электрический заряд.
– положительный пробный электрический заряд. .
. ,
, ,
, называется потенциалом поля (измеряется в вольтах – В):
называется потенциалом поля (измеряется в вольтах – В):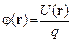 .
. .
. (
( м/с):
м/с): .
. ,
, – плотность тока;
– плотность тока;  – напряженность электрического поля между концами проводника;
– напряженность электрического поля между концами проводника;  – удельная проводимость проводника.
– удельная проводимость проводника. .
. .
. ,
, – длина проводника;
– длина проводника;  – площадь поперечного сечения проводника;
– площадь поперечного сечения проводника;  – удельное сопротивление проводника,
– удельное сопротивление проводника,  .
.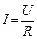 .
. .
.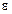 – ЭДС (электродвижущая сила) источника тока;
– ЭДС (электродвижущая сила) источника тока;  .
. .
. кг и его скорость
кг и его скорость  м/с, масса платформы с орудием
м/с, масса платформы с орудием  тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен
тонн. На какое расстояние откатится платформа после выстрела, если коэффициент трения равен  ?
? .
.
 платформы получаем:
платформы получаем: .
. , то работа силы трения равна
, то работа силы трения равна ,
, .
.
 . Итак, подставляем заготовки:
. Итак, подставляем заготовки:
 м
м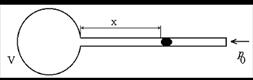
 , следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния:
, следовательно, процесс изменения температуры изобарический. Запишем для этого процесса закон Шарля, связывающий начальное и конечное состояния: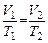 , (1)
, (1) ,
,  . Подставляем выражения для V 1 и V 2 в (1) и получаем
. Подставляем выражения для V 1 и V 2 в (1) и получаем . (2)
. (2)
 ,
,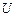 – постоянно, количество энергии
– постоянно, количество энергии 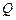 , необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что
, необходимой для нагревания воды, одинаково во всех случаях. Далее получаем, что .
.

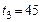 минут; б) при параллельном соединении секций
минут; б) при параллельном соединении секций  минут.
минут. , где
, где  ,
,  . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени  и
и  . Каково среднее значение скорости за первые
. Каково среднее значение скорости за первые  движения?
движения?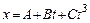 , где
, где  ,
,  ,
,  . Найти координату х, скорость Vx и ускорение ах в момент времени
. Найти координату х, скорость Vx и ускорение ах в момент времени  .
. , где
, где  ,
,  ,
,  . Найти полное ускорение точки, находящейся на расстоянии
. Найти полное ускорение точки, находящейся на расстоянии  от оси вращения, в момент времени
от оси вращения, в момент времени  .
. и
и  , где
, где  ,
,  ,
,  ,
, 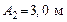 ,
, 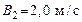 ,
,  . В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени
. В какой момент времени скорости этих точек будут одинаковы? Найти ускорения а 1 и а 2 этих точек в момент времени  .
.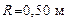 , вращающегося согласно уравнению
, вращающегося согласно уравнению  , где
, где 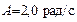 ,
,  .
. , где
, где  ,
,  . Через какое время тело остановится и сколько оборотов сделает до остановки?
. Через какое время тело остановится и сколько оборотов сделает до остановки?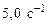 до
до  ? Угловое ускорение равно
? Угловое ускорение равно  .
.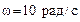 и угловым ускорением
и угловым ускорением  . Сколько оборотов сделает тело за время
. Сколько оборотов сделает тело за время 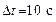 от начала движения?
от начала движения? , находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением
, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением  . Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения?
. Каковы были тангенциальное aτ, нормальное an и полное a ускорения точек, лежащих на ободе диска, в конце второй секунды после начала вращения?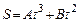 , где
, где  ,
,  . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени 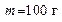 , летевший со скоростью
, летевший со скоростью 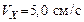 под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой.
под углом 60о к плоскости стенки, упруго ударился о неё и отскочил с той же (по модулю) скоростью. Определить импульс силы, полученный стенкой. . Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда
. Орудие выстреливает под углом 60о к линии горизонта в направлении пути. Какую скорость U приобретет платформа вследствие отдачи, если масса снаряда  и он вылетает из ствола орудия со скоростью
и он вылетает из ствола орудия со скоростью  ?
? , разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью
, разорвался на два осколка. Меньший осколок, масса которого составляет 20 % от общей массы снаряда, полетел в противоположном направлении со скоростью  . Определить скорость
. Определить скорость  большего осколка.
большего осколка. , бегущий со скоростью
, бегущий со скоростью 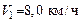 , догоняет тележку массой
, догоняет тележку массой  , движущуюся со скоростью
, движущуюся со скоростью 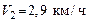 , и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу?
, и вскакивает на нее. С какой скоростью U 1 станет двигаться тележка? С какой скоростью U 2 будет двигаться тележка, если человек бежал ей навстречу? , падая с высоты
, падая с высоты  на стальную плиту, отскакивает от нее на высоту
на стальную плиту, отскакивает от нее на высоту  . Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком.
. Найти количество тепла, выделившегося при ударе, и долю от первоначальной энергии, потерянную шариком. движется со скоростью
движется со скоростью 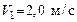 и сталкивается с покоящимся шаром массой
и сталкивается с покоящимся шаром массой  . Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным. движется со скоростью
движется со скоростью  и сталкивается с шаром массой
и сталкивается с шаром массой  , который движется ему навстречу со скоростью
, который движется ему навстречу со скоростью  . Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
. Определить скорости U 1 и U 2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.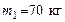 , стоя на коньках на льду, бросает в горизонтальном направлении камень массой
, стоя на коньках на льду, бросает в горизонтальном направлении камень массой  со скоростью
со скоростью  . Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед
. Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков об лед  .
. , двигавшийся со скоростью
, двигавшийся со скоростью 


