
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между потенциалом и напряженностьюСодержание книги
Поиск на нашем сайте Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: d A = q E d l, эта же работа равна убыли потенциальной энергии заряда q: d A = - d W п = - q d Ex d x + Ey d y + Ez d z = -d где Ex, Ey, Ez - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем откуда Стоящее в скобках выражение является градиентом потенциала j, т. е. E = - grad Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала. Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна т. е. в этом направлении потенциал электрического поля является постоянной величиной ( В рассмотренном случае направление вектора r совпадает с направлением силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми. Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению. ВОПРОС Электроемкость проводников - это физическая величина, характеризующая способность проводника или системы проводников накапливать электрические заряды. Еденица электроемкости - фарад (Ф).
Сообщенный проводнику заряд Q распределяется по его поверхности так, что напряженность поля внутри проводника равна нулю. Если проводнику сообщить такой же заряд Q, то он распределится по поверхности проводника. Отсюда следует, что потенциал проводника пропорционален находящемуся на нем заряду (Q = Cfi). Электроемкость проводников равна С = Q/fi. Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы. Конденсатор — это система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор. Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность между пластинами будет в два раза Польше, чем напряженность одной пластины. Вне пластин напряженность равна нулю. Обозначаются конденсаторы на схемах так:
Электроемкостью конденсатора называют величину, равную отношению величины заряда одной из пластин к напряжению между ними. Электроемкость обозначается По определению Электроемкость плоского конденсатора (рис. 16) находится по формуле:
где
В зависимости от типа диэлектрика конденсаторы бывают воздушные, бумажные, слюдяные. Конденсаторы применяются для накопления электрическоЙ энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах. ВОПРОС
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 ,где d
,где d 
 .
. .
. ,
,

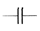 — конденсатор постоянной емкости;
— конденсатор постоянной емкости; — конденсатор переменной емкости.
— конденсатор переменной емкости. .
. . Единицей электроемкоести является фарад (Ф). 1 фарад — это электроемкость такого конденсатора, напряжение между обкладками которого равно 1 вольту при сообщении обкладкам разноименных зарядов по 1 кулону.
. Единицей электроемкоести является фарад (Ф). 1 фарад — это электроемкость такого конденсатора, напряжение между обкладками которого равно 1 вольту при сообщении обкладкам разноименных зарядов по 1 кулону. ,
, — электрическая постоянная,
— электрическая постоянная,  — диэлектрическая постоянная среды,
— диэлектрическая постоянная среды,  — площадь обкладки конденсатора,
— площадь обкладки конденсатора,  — рас-стояние между обкладками (или толщина диэлектрика).
— рас-стояние между обкладками (или толщина диэлектрика).



