
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Брюстера. Закон МалюсаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Наиболее просто поляризационный свет можно получить из естественного света при отражении световой волны от границы раздела двух диэлектриков. Если естественный свет падает на границу раздела двух диэлектриков (например, воздух-стекло), то часть его отражается, а часть преломляется и распространяется во второй среде. Закон Брюстера: При угле падения, равном углу Брюстера іБ р: 1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения; 2. степень поляризации преломленного луча достигает максимального значения меньшего единицы; 3. преломленный луч будет поляризован частично в плоскости падения; 4. угол между отраженным и преломленным лучами будет равен 90°; 4. тангенс угла Брюстера равен относительному показателю преломления
- закон Брюстера.
Степень поляризации преломленного света может быть значительно повышена многократным преломлением при условии падения света на границу раздела под углом Брюстера. Если для стекла (n = 1,53) степень поляризации преломленного луча составляет ≈15 %, то после преломления на 8-10 наложенных друг на друга стеклянных пластинках, вышедший свет будет практически полностью поляризован - стопа Столетова. Поляризованный свет можно получить из естественного с помощью поляризаторов - анизотропных кристаллов, пропускающих свет только в одном направлении (исландский шпат, кварц, турмалин). Поляризатор, анализирующий в какой плоскости поляризован свет, называется анализатором.
Сквозь анализатор пройдет составляющая параллельная плоскости анализатора, то есть составляющая
Закон Малюса: Интенсивность света, прошедшего через поляризатор, прямо пропорциональна произведению интенсивности падающего плоско поляризованного света I 0 и квадрату косинуса угла между плоскостью падающего света и плоскостью поляризатора. Если на поляризатор падает естественный свет, то интенсивность вышедшего из поляризатора света I 0 равна половине I ест, и тогда из анализатора выйдет
Вопрос Теплово́е излуче́ние — электромагнитное излучение, возникающее за счёт внутренней энергии тела[1]. Имеет сплошной спектр, максимум которого зависит от температуры тела. При остывании последний смещается в длинноволновую часть спектра. Тепловое излучение имеет нагретый металл, земная атмосфера, белый карлик[1][2]. Примером механизма, приводящего к тепловому излучению может служить тормозное излучение или ударное возбуждение атомных уровней с последующим высвечиванием. Характерной чертой является то, что при усреднении коэффициента излучения по максвелловскому распределению, начиная с энергий hν~kT, в спектре начинается экспоненциальный завал.[3] В случае, если излучение находится в термодинамическом равновесии с веществом, то такое излучение называется равновесным. Спектр такого излучения эквивалентен спектру абсолютно черного тела и описывается законом Планка. Однако в общем случае тепловое излучение не находится в термодинамическом равновесии с веществом, таким образом более горячее тело остывает, а более холодное наоборот нагревается. Спектр такого излучения определяется законом Кирхгофа. Энергетическая светимость тела[править | править исходный текст] Энергетическая светимость тела -
Спектральная плотность энергетической светимости[править | править исходный текст] Спектральная плотность энергетической светимости — функция частоты и температуры, характеризующая распределение энергии излучения по всему спектру частот (или длин волн).
Аналогичную функцию можно написать и через длину волны
Можно доказать, что спектральная плотность энергетической светимости, выраженная через частоту и длину волны, связаны соотношением:
Поглощающая способность тела[править | править исходный текст] Поглощающая способность тела —
где
Отражающая способность тела[править | править исходный текст] Отражающая способность тела —
где
Подробнее Альбедо Абсолютно чёрное тело[править | править исходный текст] Абсолютно черное тело — это физическая абстракция (модель), под которой понимают тело, полностью поглощающее всё падающее на него электромагнитное излучение
Подробнее Абсолютно черное тело Серое тело[править | править исходный текст] Серое тело — это такое тело, коэффициент поглощения которого не зависит от частоты, а зависит только от температуры
Объемная плотность энергии излучения[править | править исходный текст] Объемная плотность энергии излучения — Спектральная плотность энергии[править | править исходный текст] Спектральная плотность энергии —
Следует отметить, что спектральная плотность энергетической светимости для абсолютно чёрного тела связана со спектральной плотностью энергии следующим соотношением:
Основные законы теплового излучения[править | править исходный текст] · Закон Стефана — Больцмана · Закон излучения Кирхгофа · Закон смещения Вина · Закон излучения Кирхгофа — физический закон, установленный немецким физиком Кирхгофом в 1859 году. · В современной формулировке закон звучит следующим образом: · Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы. · Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела · Величины · · По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него · Реальные тела имеют поглощательную способность меньше единицы, а значит, и меньшую чем у абсолютно чёрного тела излучательную способность. Тела, поглощательная способность которых не зависит от частоты, называются серыми. Их спектр имеет такой же вид, как и у абсолютно чёрного тела. В общем же случае поглощательная способность тел зависит от частоты и температуры, и их спектр может существенно отличаться от спектра абсолютно чёрного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения — куба Лесли. · Применения закона Кирхгофа[править | править исходный текст] · В астрофизике[править | править исходный текст] · В астрофизике закон Кирхгофа часто применяется в следующем виде: · · где · Закон Кирхгофа справедлив только для случаев теплового равновесия. Однако, его часто применяют и для неравновесных систем, когда излучение не находится в равновесии с веществом и его распределение по частотам существенно отличается от планковского. При этом часто (но не всегда) предположение отермодинамическом равновесии между частицами излучающего вещества оказывается хорошим приближением. Степень отклонения от закона Кирхгофа может служить мерой отличия излучения космических объектов от теплового. Вопрос Абсолютно чёрное тело — физическая идеализация, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой. Важность абсолютно чёрного тела в вопросе о спектре теплового излучения любых (серых и цветных) тел вообще, кроме того, что оно представляет собой наиболее простой нетривиальный случай, состоит ещё и в том, что вопрос о спектре равновесного теплового излучения тел любого цвета и коэффициента отражения сводится методами классической термодинамики к вопросу об излучении абсолютно чёрного тела (и исторически это было уже сделано к концу XIX века, когда проблема излучения абсолютно чёрного тела вышла на первый план). Наиболее чёрные реальные вещества, например, сажа, поглощают до 99 % падающего излучения (то есть имеют альбедо, равное 0,01) в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже. Среди тел Солнечной системы свойствами абсолютно чёрного тела в наибольшей степени обладает Солнце. Термин был введён Густавом Кирхгофом в 1862 году. Первый закон излучения Вина[править | править исходный текст] В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу: · где u ν — плотность энергии излучения, ν — частота излучения, T — температура излучающего тела, f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений. Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина. Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы. Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума. Второй закон излучения Вина[править | править исходный текст] В 1896 году Вин, на основе дополнительных предположений, вывел второй закон:
где C 1, C 2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина. Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C 1 и C 2. С учётом этого, второй закон Вина можно записать в виде:
где h — постоянная Планка, k — постоянная Больцмана, c — скорость света в вакууме. Закон Рэлея — Джинса[править | править исходный текст] Основная статья: закон Рэлея — Джинса Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой. Тем не менее закон излучения Рэлея — Джинса справедлив для длинноволновой области спектра и адекватно описывает характер излучения. Объяснить факт такого соответствия можно лишь при использовании квантово-механического подхода, согласно которому излучение происходит дискретно. Исходя из квантовых законов можно получить формулу Планка, которая будет совпадать с формулой Рэлея — Джинса при Этот факт является прекрасной иллюстрацией действия принципа соответствия, согласно которому новая физическая теория должна объяснять всё то, что была в состоянии объяснить старая. Закон Планка[править | править исходный текст] Основная статья: Формула Планка Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:
где Эквивалентно,
где Полная (т.е. испускаемая во всех направлениях) спектральная мощность излучения с единицы поверхности абсолютно чёрного тела описывается этими же формулами с точностью до коэффициента π: ε(ν, T) = π I (ν, T), ε(λ, T) = π u (λ, T)[1]. Закон Стефана — Больцмана[править | править исходный текст] Основная статья: Закон Стефана — Больцмана Общая энергия теплового излучения определяется законом Стефана — Больцмана, который гласит: Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:
где
Таким образом, абсолютно чёрное тело при Для нечёрных тел можно приближённо записать:
где Константу Стефана — Больцмана Закон смещения Вина[править | править исходный текст]
Зависимость мощности излучения чёрного тела от длины волны Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:
где Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра). Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме. Чернотельное излучение[править | править исходный текст] Электромагнитное излучение, находящееся в термодинамическом равновесии с абсолютно чёрным телом при данной температуре (например, излучение внутри полости в абсолютно чёрном теле), называется чернотельным (или тепловым равновесным) излучением. Равновесное тепловое излучение однородно, изотропно и неполяризовано, перенос энергии в нём отсутствует, все его характеристики зависят только от температуры абсолютно чёрного тела-излучателя (и, поскольку чернотельное излучение находится в тепловом равновесии с данным телом, эта температура может быть приписана излучению). Объёмная плотность энергии чернотельного излучения равна Цветность чернотельного излучения[править | править исходный текст]
Цвета даны в сравнении с рассеянным дневным светом (D65). Реально воспринимаемый цвет может быть искажён адаптацией глаза к условиям освещения. Вопрос В современной трактовке гипотеза квантов утверждает, что энергия E колебаний атома или молекулы может быть равна h ν, 2 h ν, 3 h ν и т.д., но не существует колебаний с энергией в промежутке между двумя последовательными целыми, кратными. Это означает, что энергия не непрерывна, как полагали на протяжении столетий, а квантуется, т.е. существует лишь в строго определенных дискретных порциях. Наименьшая порция называется квантом энергии. Гипотезу квантов можно сформулировать и как утверждение о том, что на атомно-молекулярном уровне колебания происходят не с любыми амплитудами. Допустимые значения амплитуды связаны с частотой колебания ν. В 1905 г. Эйнштейн выдвинул смелую идею, обобщавшую гипотезу квантов, и положил ее в основу новой теории света (квантовой теории фотоэффекта). Согласно теории Эйнштейна, свет с частотой νне только испускается, как это предполагал Планк, но и распространяется и поглощается веществом отдельными порциями (квантами), энергия которых. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью распространения света в вакууме (с). Квант электромагнитного излучения получил название фотон. Как мы уже говорили, испускание электронов с поверхности металла под действием падающего на него излучения соответствует представлению о свете как об электромагнитной волне, т.к. электрическое поле электромагнитной волны воздействует на электроны в металле и вырывает некоторые из них. Но Эйнштейн обратил внимание на то, что предсказываемые волновой теорией и фотонной (квантовой корпускулярной) теорией света детали фотоэффекта существенно расходятся. Итак, мы можем измерить энергию вылетевшего электрона, исходя из волновой и фотонной теории. Чтобы ответить на вопрос, какая теория предпочтительней, рассмотрим некоторые детали фотоэффекта. Начнем с волновой теории, и предположим, что пластина освещается монохроматическим светом. Световая волна характеризуется параметрами: интенсивностью и частотой (или длиной волны). Волновая теория предсказывает, что при изменении этих характеристик происходят следующие явления: · при увеличении интенсивности света число выбитых электронов и их максимальная энергия должны возрастать, т.к. более высокая интенсивность света означает большую амплитуду электрического поля, а более сильное электрическое поле вырывает электроны с большей энергией; выбитых электронов; кинетическая энергия зависит только от интенсивности падающего света. Совершенно иное предсказывает фотонная (корпускулярная) теория. Прежде всего, заметим, что в монохроматическом пучке все фотоны имеют одинаковую энергию (равную h ν). Увеличение интенсивности светового пучка означает увеличение числа фотонов в пучке, но не сказывается на их энергии, если частота остается неизменной. Согласно теории Эйнштейна, электрон выбивается с поверхности металла при соударении с ним отдельного фотона. При этом вся энергия фотона передается электрону, а фотон перестает существовать. Т.к. электроны удерживаются в металле силами притяжения, для выбивания электрона с поверхности металла требуется минимальная энергия A (которая называется работой выхода и составляет, для большинства металлов, величину порядка нескольких электронвольт). Если частота ν падающего света мала, то энергии и энергии фотона недостаточно для того, чтобы выбить электрон с поверхности металла. Если же, то электроны вылетают с поверхности металла, причем энергия в таком процессе сохраняется, т.е. энергия фотона (h ν) равна кинетической энергии вылетевшего электрона плюс работе по выбиванию электрона из металла:
Уравнение (2.3.1) называется уравнением Эйнштейна для внешнего фотоэффекта. На основе этих соображений, фотонная (корпускулярная) теория света предсказывает следующее. 1. Увеличение интенсивности света означает увеличение числа налетающих фотонов, которые выбивают с поверхности металла больше электронов. Но так как энергия фотонов одна и та же, максимальная кинетическая энергия электрона не изменится (подтверждается I закон фотоэффекта). 2. При увеличении частоты падающего света максимальная кинетическая энергия электронов линейно возрастает в соответствии с формулой Эйнштейна (2.3.1). (Подтверждение II закона фотоэффекта). График этой зависимости представлен на рис. 2.3.
3. Если частота ν меньше критической частоты, то выбивание электронов с поверхности не происходит (III закон). Итак, мы видим, что предсказания корпускулярной (фотонной) теории сильно отличаются от предсказаний волновой теории, но очень хорошо совпадают с тремя экспериментально установленными законами фотоэффекта. Уравнение Эйнштейна было подтверждено опытами Милликена, выполненными в 1913–1914 гг. Основное отличие от опыта Столетова в том, что поверхность металла подвергалась очистке в вакууме. Исследовалась зависимость максимальной кинетической энергии от частоты и определялась постоянная Планка h. В 1926 г. российские физики П.И. Лукирский и С.С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора. Анодом служили посеребренные стенки стеклянного сферического баллона, а катодом – шарик (R ≈ 1,5 см) из исследуемого металла, помещенного в центр сферы. Такая форма электродов позволяла увеличить наклон ВАХ и тем самым более точно определить задерживающее напряжение (а следовательно, и h). Значение постоянной Планка h, полученное из этих опытов, согласуется со значениями, найденными другими методами (по излучению черного тела и по коротковолновой границе сплошного рентгеновского спектра). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта. Для объяснения теплового излучения Планк предположил, что свет испускается квантами. Эйнштейн при объяснении фотоэффекта предположил, что свет поглощается квантами. Также Эйнштейн предположил, что свет и распространяется квантами, т.е. порциями. Квант световой энергии получил название фотон. Т.е. опять пришли к понятию корпускула (частица). Наиболее непосредственное подтверждение гипотезы Эйнштейна дал опыт Боте, в котором использовался метод совпадения (рис. 2.4).
Тонкая металлическая фольга Ф помещалась между двумя газоразрядными счетчиками Сч. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление называется рентгеновской флуоресценцией). Вследствие малой интенсивности первичного пучка, количество квантов, испускаемых фольгой, было невелико. При попадании квантов на счетчик механизм срабатывал и на движущейся бумажной ленте делалась отметка. Если бы излучаемая энергия распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении. Так было экспериментально доказано существование особых световых частиц – фотонов. Фотон обладает энергией. Для видимого света длина волны λ = 0,5 мкм и энергия Е = 2,2 эВ, для рентгеновских лучей λ = мкм и Е = 0,5 эВ. Фотон обладает инертной массой, которую можно найти из соотношения:
Фотон движется со скоростью света c = 3·108 м/с. Подставим это значение скорости в выражение для релятивистской массы:
Фотон – частица, не обладающая массой покоя. Она может существовать, только двигаясь со скоростью света c. Найдем связь энергии с импульсом фотона. Мы знаем релятивистское выражение для импульса:
И для энергии:
Из (2.3.3) найдем:
Подставив выражение (2.3.5) в выражение для энергии (2.3.4), получим связь между энергией и импульсом:
Или
Но т. к. для покоящегося фотона,. Окончательно получим:
Т.к., то можно записать:
Обозначим где k – волновое число. Теперь выразим импульс через волновой вектор:
Вопрос Фотоэффе́кт, Фотоэлектрический эффект — испускание электронов веществом под действием света (или любого другогоэлектромагнитного излучения). В конденсированных (твёрдых и жидких) веществах выделяют внешний и внутренний фотоэффект. Законы Столетова для фотоэффекта: Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока. Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности. 3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией h ν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода φ, покидает металл: История открытия[править | править исходный текст] В 1839 году Александр Беккерель наблюдал[1] явление фотоэффекта в электролите. В 1873 году Уиллоуби Смит обнаружил, что селен является фотопроводящим. Затем эффект изучался в 1887 году Генрихом Герцем. При работе с открытым резонатором он заметил, что если посветить ультрафиолетом на цинковые разрядники, то прохождение искры заметно облегчается. Исследования фотоэффекта показали, что, вопреки классической электродинамике, энергия вылетающего электрона всегда строго связана с частотой падающегоизлучения и практически не зависит от интенсивности облучения. В 1888—1890 годах фотоэффект систематически изучал русский физик Александр Столетов. Им были сделаны несколько важных открытий в этой области, в том числе выведен первый закон внешнего фотоэффекта.
Схема эксперимента по исследованию фотоэффекта. Из света берётся узкий диапазон частот и направляется на катодвнутри вакуумного прибора. Напряжением между катодом и анодом устанавливается энергетический порог между ними. По току судят о достижении электронами анода. Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Карла Вильгельма Озеена, получил Нобелевскую премию) на основе гипотезы Макса Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк в 1900 году предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фот
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 3615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.012 с.) |


 n12 - показатель преломления второй среды относительно первой. Угол падения (отражения) - угол между падающим (отраженным) лучом и нормалью к поверхности. Плоскость падения - плоскость, проходящая через падающий луч и нормаль к поверхности.
n12 - показатель преломления второй среды относительно первой. Угол падения (отражения) - угол между падающим (отраженным) лучом и нормалью к поверхности. Плоскость падения - плоскость, проходящая через падающий луч и нормаль к поверхности. Если на анализатор падает плоско поляризованный свет амплитудой Е 0 и интенсивности I 0 (
Если на анализатор падает плоско поляризованный свет амплитудой Е 0 и интенсивности I 0 ( ), плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами
), плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами  и
и  ,параллельное и перпендикулярное плоскости анализатора.
,параллельное и перпендикулярное плоскости анализатора. ):
): - закон Малюса
- закон Малюса


 — физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.
— физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот. ;
;  Дж/с·м² = Вт/м²
Дж/с·м² = Вт/м²


 — функция частоты и температуры, показывающая, какая часть энергии электромагнитного излучения, падающего на тело, поглощается телом в области частот
— функция частоты и температуры, показывающая, какая часть энергии электромагнитного излучения, падающего на тело, поглощается телом в области частот  вблизи
вблизи 

 — поток энергии, поглощающейся телом.
— поток энергии, поглощающейся телом. — поток энергии, падающий на тело в области
— поток энергии, падающий на тело в области 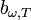 — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот
— функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот 
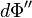 — поток энергии, отражающейся от тела.
— поток энергии, отражающейся от тела. — для абсолютно чёрного тела
— для абсолютно чёрного тела — для серого тела
— для серого тела — функция температуры, численно равная энергии электромагнитного излучения в единицу объёма по всему спектру частот
— функция температуры, численно равная энергии электромагнитного излучения в единицу объёма по всему спектру частот — функция частоты и температуры, связанная с объемной плотностью излучения формулой:
— функция частоты и температуры, связанная с объемной плотностью излучения формулой:
 — для абсолютно чёрного тела
— для абсолютно чёрного тела . С другой стороны, каждое нагретое тело излучает энергию по некоторому закону
. С другой стороны, каждое нагретое тело излучает энергию по некоторому закону  , именуемым излучательной способностью тела.
, именуемым излучательной способностью тела.
 . Поэтому функция
. Поэтому функция  совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности. ,
, — коэффициент излучения (энергия, излучаемая единичным объёмом в единичном интервале частот в единичный телесный угол за единицу времени);
— коэффициент излучения (энергия, излучаемая единичным объёмом в единичном интервале частот в единичный телесный угол за единицу времени);  —коэффициент поглощения с учётом вынужденного испускания (
—коэффициент поглощения с учётом вынужденного испускания ( , где
, где  — плотность вещества, а
— плотность вещества, а 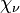 и
и  — соответственно непрозрачность и эффективная длина пробега фотонов для частоты
— соответственно непрозрачность и эффективная длина пробега фотонов для частоты  );
); 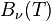 — интенсивность излучения абсолютно чёрного тела.
— интенсивность излучения абсолютно чёрного тела.
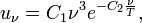

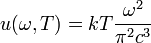
 .
.
 — мощность излучения на единицу площади излучающей поверхности в единичном интервале частот в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·Гц−1·ср−1).
— мощность излучения на единицу площади излучающей поверхности в единичном интервале частот в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·Гц−1·ср−1).
 — мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·м−1·ср−1).
— мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·м−1·ср−1).
 — мощность на единицу площади излучающей поверхности, а
— мощность на единицу площади излучающей поверхности, а Вт/(м²·К4) — постоянная Стефана — Больцмана.
Вт/(м²·К4) — постоянная Стефана — Больцмана. = 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.
= 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.
 — степень черноты (для всех веществ
— степень черноты (для всех веществ  , для абсолютно чёрного тела
, для абсолютно чёрного тела  ).
).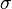 можно теоретически вычислить только из квантовых соображений, воспользовавшись формулой Планка. В то же время общий вид формулы может быть получен из классических соображений (что не снимает проблемы ультрафиолетовой катастрофы).
можно теоретически вычислить только из квантовых соображений, воспользовавшись формулой Планка. В то же время общий вид формулы может быть получен из классических соображений (что не снимает проблемы ультрафиолетовой катастрофы).

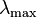 — длина волны с максимальной интенсивностью в метрах.
— длина волны с максимальной интенсивностью в метрах.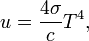 его давление равно
его давление равно  Очень близко по своим свойствам к чернотельному так называемое реликтовое излучение, или космический микроволновой фон — заполняющее Вселенную излучение с температурой около 3 К.
Очень близко по своим свойствам к чернотельному так называемое реликтовое излучение, или космический микроволновой фон — заполняющее Вселенную излучение с температурой около 3 К. (или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если
(или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если  , то фотоэффект уже не происходит.
, то фотоэффект уже не происходит. где
где  — максимальная кинетическая энергия, которую имеет электрон при вылете из металла.
— максимальная кинетическая энергия, которую имеет электрон при вылете из металла.



