
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа сил электростатического поля. ПотенциалСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрическое поле, подобно гравитационному, является потенциальным. Т.е. работа, выполняемая электростатическими силами, не зависит от того, по какому маршруту заряд q перемещен в электрическом поле из точки 1 в точку 2. Эта работа равна разности потенциальных энергий, которыми обладает перемещаемый заряд в начальной и конечной точках поля: А1,2 = W1 – W2. (7)
Можно показать, что потенциальная энергия заряда q прямо пропорциональна величине этого заряда. Поэтому в качестве энергетической характеристики электростатического поля используется отношение потенциальной энергии пробного заряда q0, помещенного в какую-либо точку поля, к величине этого заряда:
Эта величина представляет собой количество потенциальной энергии на единицу положительного заряда и называется потенциалом поля в заданной точке. [φ] = Дж / Кл = В (Вольт). Если принять, что при удалении заряда q0 в бесконечность (r→ ∞) его потенциальная энергия в поле заряда q обращается в нуль, то потенциал поля точечного заряда q на расстоянии r от него:
Если поле создаётся системой точечных зарядов, то потенциал результирующего поля равен алгебраической (с учётом знаков) сумме потенциалов каждого из них:
Из определения потенциала (8) и выражения (7) работа, совершаемая силами электростатического поля по перемещению заряда из
точки 1 в точку 2, может быть представлена как:
НАПРЯЖЁННОСТЬ КАК ГРАДИЕНТ ПОТЕНЦИАЛА Найдем взаимосвязь между напряженностью Е электростатического поля, являющейся его силовой характеристикой, и потенциалом φ – энергетической характеристикой поля. Работа по перемещению точечного, положительного заряда q вдоль произвольного направления х из точки 1 в бесконечно близкую к ней точку 2, х 2 – х 1 = d х, будет равна: А1,2 = q· Е х ∙d х или через потенциал: А1,2 = q(φ1 – φ2) = - q ·dφ. Откуда:
т.е. напряженность поля равна градиенту потенциала, взятому со знаком минус. Это означает, что Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхность, во всех точках которой потенциал φ имеет одно и то же значение. Для точечных зарядов в однородной среде, например, эти поверхности представляют собой сферы (рис.133а Трофимова, стр139). Для любой точки поля линии напряженности всегда направлены по нормали к эквипотенциальным поверхностям. (рис.133б Трофимова, стр139).
Э Л Е К Т Р И Ч Е С К И Й Д И П О Л Ь
Электрический диполь – система двух равных по величине разноименных точечных зарядов +q и -q, расстояние
называется электрическим моментом диполя или дипольным моментом. Определим потенциал и напряженность поля диполя в произвольной точке M на расстоянии r от середины диполя. Потенциал поля в точке М:
Учитывая, что l ‹‹ r, r+ ≈ r- = r и r- – r+ ≈ l cos(π-θ), окончательно для φ получим:
В соответствии с принципом суперпозиции напряженность поля диполя
Э Н Е Р Г И Я Э Л Е К Т Р О С Т А Т И Ч С К О Г О П О Л Я
Определим объёмную плотность энергии электрического поля. Для этого рассмотрим процесс зарядки плоского конденсатора, как работу по разделению зарядов между обкладками. Перенесём заряд dq с одной обкладки на другую. Работа dА, которая при этом будет совершена: dА = dq∙u = C∙u∙du, (17)
где u – мгновенное значение разности потенциалов на конденсаторе, С – его ёмкость. Проинтегрируем правую и левую часть равенства:
С учётом формулы для электроёмкости плоского конденсатора, получим:
где V – объём конденсатора, Е – напряжённость поля, а ε – диэлектрическая проницаемость среды между обкладками. Выражение
определяет энергию единицы объёма поля и называется объёмной плотностью энергии поля.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1032; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

 . (8)
. (8) . (9)
. (9) . (10)
. (10) (11)
(11) , (12)
, (12) направлен в сторону убывания потенциала.
направлен в сторону убывания потенциала. между которыми значительно меньше расстояния до рассматриваемых точек поля. Прямая, проходящая через оба заряда, называется осью диполя. Вектор
между которыми значительно меньше расстояния до рассматриваемых точек поля. Прямая, проходящая через оба заряда, называется осью диполя. Вектор  , направленный от отрицательного заряда к положительному и равный по модулю расстоянию между ними, называется плечом диполя. Вектор
, направленный от отрицательного заряда к положительному и равный по модулю расстоянию между ними, называется плечом диполя. Вектор 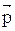 ,
,
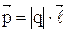 , (13)
, (13) (14)
(14) . (15)
. (15) . Вывод формулы для модуля напряженности поля диполя более сложен. Запишем эту формулу без вывода:
. Вывод формулы для модуля напряженности поля диполя более сложен. Запишем эту формулу без вывода: (16)
(16) . (18)
. (18) , (19)
, (19) (20)
(20)


