
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постоянный электрический токСодержание книги Поиск на нашем сайте Электрическим током называется любое упорядоченное дви-жение заряженных частиц. Ток в проводнике под воздействием электрического поля называется током проводимости. Количественной мерой этого процесса является скалярная величина, которая называется сила тока:
где i – мгновенное значение силы тока в проводнике, dq – заряд, протекающего через его поперечное сечение за время dt. [I] = Kл/c = А. Постоянным, называется электрический ток, сила и направление которого не меняются с течением времени. За направление тока условились принимать направление движения положительных зарядов. Величина, равная силе тока протекающего через единицу площади поперечного сечения, называется плотностью тока:
Выразим i и j через среднюю скорость жения зарядов одного знака (скорость дрейфа). Пусть величина каждого заряда – q0, а их концентрация (число частиц в единице объёма) в проводнике – n. Tогда за время dt через участок с поперечным сечением проводника dS пройдет заряд:
Интегрируя по времени, получим для тока через площадку dS:
Это даёт для плотности тока на участке с поперечным сечением dS:
Сумма произведений j∙dS по всем участкам поверхности S даёт величину силы тока через произвольную поверхность:
Если в цепи на частицы действуют только силы электрического поля, то положительные носители заряда будут перемещаться от точек с бóльшим потенциалом к точкам с меньшим потенциалом. Соответственно, отрицательные – от точек с меньшим к точкам с бóльшим потенциалом. Это приводит к выравниванию потенциала вдоль цепи и исчезновению электрического поля. Для существования тока в течение длительного промежутка времени необходимо наличие в цепи устройства способного создавать и поддерживать на отдельных участках цепи разность потенциалов. Такое устройство должно перемещать (т.е. возвращать) положительные заряды из точек с меньшим в точки с бóльшим потенциалом, а отрицательных из точек с бóльшим потенциалом в точки с меньшим. Это может быть сделано только за счет работы сил не электрического происхождения. Такие силы называются сторонними, а устройства способные выполнять такую работу – источниками тока. Природа этих сил может быть самой различной: в гальванических элементах это энергия химических реакций, в фотоэлементах – энергия солнечного света, в генераторах – механическая энергия. Работа по перемещению единичного, положительного заряда, совершаемая сторонними силами, называется электродвижущей силой (ЭДС) источника тока:
А1,2 = q(φ1 – φ2) + qξ. (8) Величина
называется напряжением на участке 1 – 2. Если ЭДС на участке цепи отсутствует, то U1.2 = (φ1 – φ2). (10)
ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению:
где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением
где γ = 1 / ρ – удельная электропроводность материала, ρ – удельное сопротивление, S – площадь поперечного сечения проводника,
Теперь для плотности тока (2) с учётом, что
Выражение (14) в векторной форме это закон Ома в дифференциальной форме:
Получим в дифференциальной форме закон Джоуля-Ленца. Количество теплоты, выделяющееся в элементе проводника, объёмом
Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет:
Эта величина называется удельной тепловой мощностью тока.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , (1)
, (1)
 (2)
(2) упорядоченного дви-
упорядоченного дви- . (3)
. (3) . (4)
. (4) или в векторной форме
или в векторной форме  . (5)
. (5) . (6)
. (6) . (7)
. (7) Эта физическая величина является энергетической характеристикой источника тока. Работа по перемещению заряда q на неоднородном участке (участке, содержащем источник тока, рис.4) в общем случае будет складываться из работы сил электростатического поля и работы сторонних сил:
Эта физическая величина является энергетической характеристикой источника тока. Работа по перемещению заряда q на неоднородном участке (участке, содержащем источник тока, рис.4) в общем случае будет складываться из работы сил электростатического поля и работы сторонних сил: (9)
(9) , (11)
, (11) , (12)
, (12) – его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид:
– его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид: . (13)
. (13) – напряжённость поля в проводнике, получим:
– напряжённость поля в проводнике, получим: . (14)
. (14)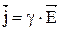 . (15)
. (15) за время dt:
за время dt: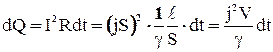 . (16)
. (16) . (17)
. (17)


